Volver Indice Ayuda
Medición de Avance de un Proyecto $AP$
Sea $\mathit{AP}$ una medida porcentual que determina el avance de un proyecto, donde
esta medición se define a partir de la razón, - llamemos $\mathbb{\large{\mathit{r}}}$ -, que es el cociente entre el número de
hitos finalizados y el número total de hitos del proyecto.
El avance $\mathit{AP}$ se expresa en porcentaje, por eso la expresión resultante
$\mathbb{\large{\mathit{r}}}\text{ }$ se multiplica por $100$, donde $ 0 \le \mathbb{\large{\mathit{r}}}
\le 1 \text{, con } \mathbb{\large{\mathit{r}}}\in R$.
Nótese que los denominadores de todas las expresiones matemáticas, tales como
totales de N° Hitos, N° Subproyectos,... se asumen mayores que cero. Es decir,
los denominadores son diferentes de cero en las formulaciones a continuación:
|
$$AP=\frac{\text{N°Hitos Finalizados del Proyecto }}{\text{N°de Total Hitos
del Proyecto}}\text{·}100\qquad(1)$$ |
|
|
Por tanto, el Avance de Proyecto $\mathit{AP}$ se define en
función de los hitos, independientemente de su distribución en los subproyectos del proyecto.
Medición de Avance de un Subproyecto $AS$
Para medir el avance de un subproyecto $AS_i$, se utiliza el
mismo modelo de fórmula, pero limitada al subproyecto $i$:
|
$$AS_i=\frac{\text{N°Hitos Finalizados del Subproyecto $i$ }}{\text{N°de Total
Hitos del Subproyecto}}\text{·}100\qquad(2)$$
|
|
|
Medición de $\mathit{AP}$ en función de los subproyectos $AS_i$
Ahora, si se mide el avance de un proyecto $\mathit{AP}$ en
función de los avances de sus subproyectos $AS_i$, entonces este avance
$AP=F(AS_i)$, se calcula mediante el promedio ponderado de los
subproyectos.
Cada ponderador señala el peso asociado al número de hitos finalizados
que tenga cada subproyecto. La fórmula se presenta de la siguiente
manera:
|
$$AP=\sum_{i=1}^n \beta_i \text{·} AS_i\qquad (3)$$
|
|
|
Donde:
| $\mathit{AP}$ : |
Avance de Proyecto medido en porcentaje $(1)$ |
|
| $n$ : |
Nº de subproyectos en el proyecto. |
|
| $\beta_i$ : |
Ponderador (razón del N° de Hitos en cada
subproyecto $S_i$ sobre el N° Total de Hitos. |
|
| $AS_i$ : |
Avance Subproyecto $i$ en porcentaje $(2)$ |
|
| $i$ : |
Indice de la sumatoria, $i = 1,2,3,\dots n$ |
|
Ejemplo:
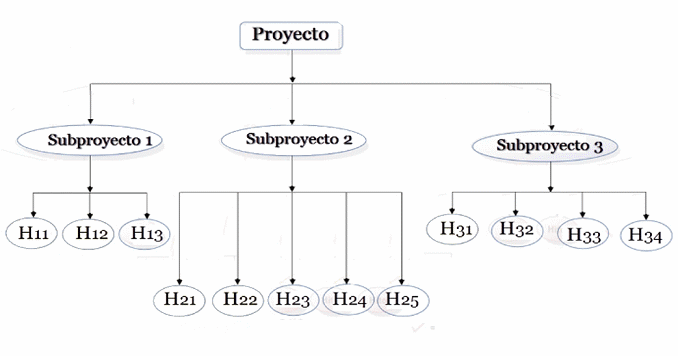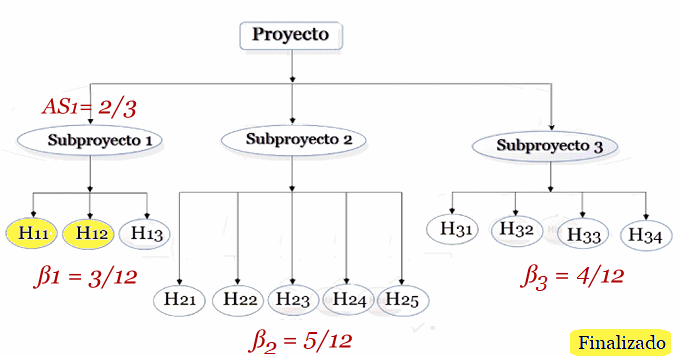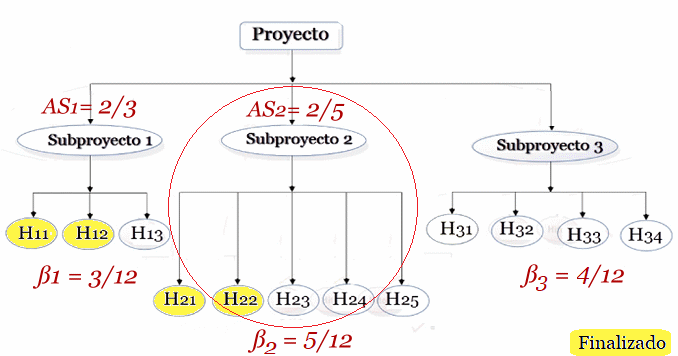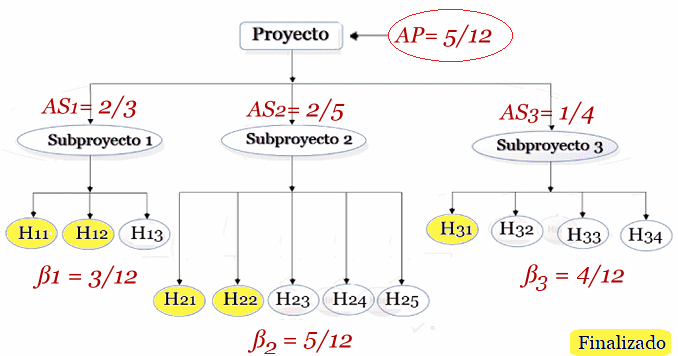
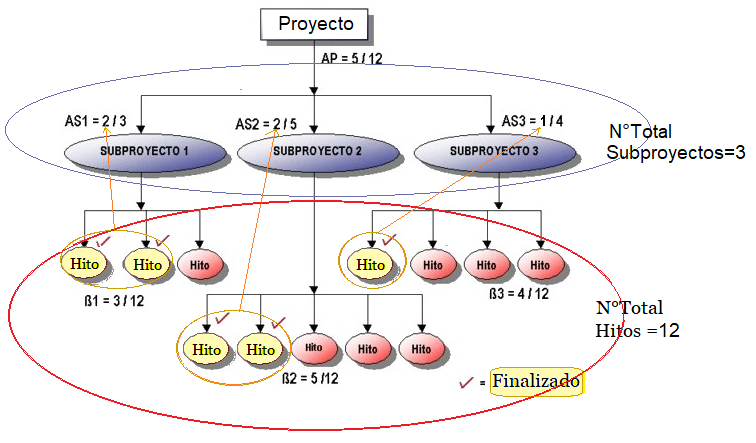Figura #1: Diagrama: Pro$\supset$ SubPro $\supset$ Hito
Supongamos un proyecto que contiene 12 hitos en total,
con 3 subproyectos, donde se han finalizado 5 hitos del total. La
distribución de los hitos y su término es:
| Subproyecto |
Total Hitos Subproyecto |
Hitos Finalizados |
| 1 |
3 |
2 |
| 2 |
5 |
2 |
| 3 |
4 |
1 |
| Total SubProyectos = 3 |
Total Hitos = 12 |
Total Hitos finalizados = 5 |
Aplicando la formula $(1)$ se obtiene directamente el avance del proyecto:
|
$$AP=\frac{5}{12}\text{·}100=\text{41,67%}$$
|
|
Aplicando la formula $(2)$obtenemos los avances individuales para cada
subproyecto:
$AS_1= \frac {2}{3} · 100= 66,67$%
$AS_2= \frac {2}{5} · 100= 40,00$%
$AS_3= \frac {1}{4} · 100= 25,00$%
Donde los indicadores de avance $AS_i$ son: {$\frac {2}{3},\frac
{2}{5}, \frac {1}{4}$} (Ver Figura#1)
Obsérvese que la estructura del ejemplo
se ilustra de la siguiente manera en un diagrama de árbol:
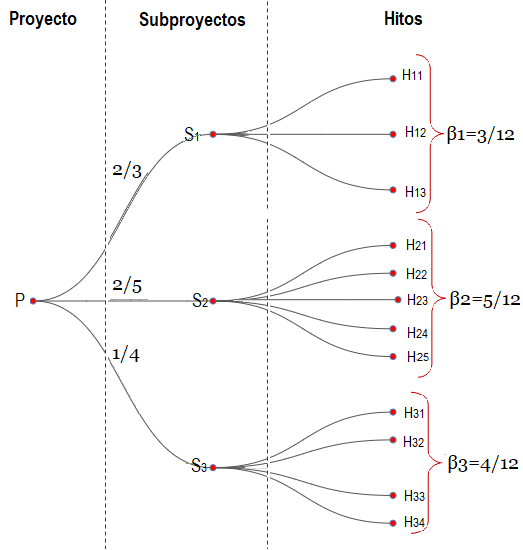Figura#2: Diagrama de Arbol del Ejemplo
y Notación de Hitos 
Desde las Figura #1 y Figura #2 se deduce que los ponderadores $\beta_i$ son una distribución por subproyectosde los hitos, los cuales se
asocian a los avance de los subproyectos $AS_i$, con $i=1,2,3$ son:
$$\beta_1=\frac {3}{12},\beta_2=\frac {5}{12}, \beta_3=\frac {4}{12}$$
Aplicando la formula $(3)$ para calcular el Avance del Proyecto, $\mathit{AP}$ en
función de los avances de los subproyectos se tiene:
$AP = (\beta_1· AS_1 + \beta_2· AS_2 + \beta_3· AS_3)·100$
$AP = (\frac {3}{12}·AS_1 + \frac{5}{12}·AS_2 + \frac{4}{12}·AS_3)·100$
$AP =\require{cancel} (\frac{\cancel{3}}{12}\frac{2}{\cancel{3}}·100 +
\frac{\cancel{5}}{12}\frac{2}{\cancel{5}} + \frac{\cancel{4}}{12}\frac{1}{\cancel{4}})·100$
$\Rightarrow $
$AP = \frac{200}{12} + \frac{200}{12} + \frac{100}{12} = \frac{500}{12}
= 41,67\text{%}$
Video Avance de Proyectos
 Video Explicativo Métrica Avance Proyectos
Ejemplo de Ficha de Proyecto
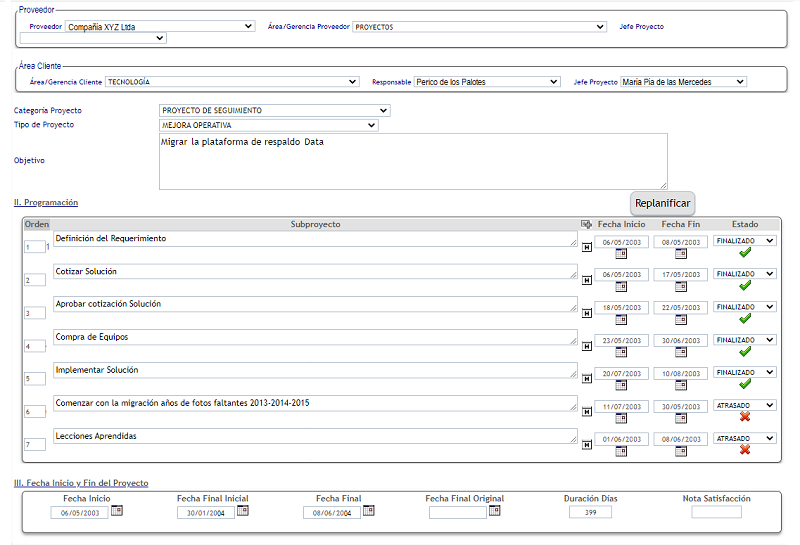 Figura
#3: Ejemplo Ficha (Ver Informe Detallado)
Luego, el Avance de Proyecto $\mathit{AP}$ es igual bajo los dos
métodos de cálculo $(1)$
y $(3)$
El avance de un proyecto determinado y sus subproyectos
se visualiza en
¿Cómo Obtener un Informe Detallado?
Ejemplo con Gráfica Gauge
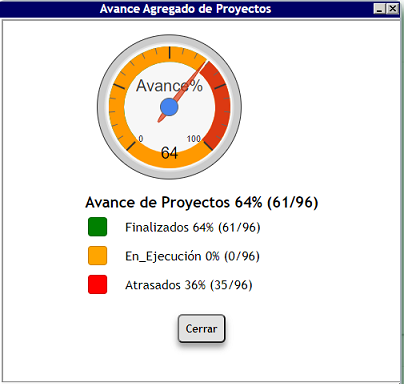 Figura
#4: Avance Agregado de Proyectos
|
Nota del Autor:
El presente enfoque de medición es lineal, simple
y netamente numérico en términos de cardinalidad, haciendo abstracción de una
serie de restricciones, definiciones y variables. Especialmente, sin incorporar
el parámetro tiempo.
En otros términos, en el presente enfoque un hito finalizado binariamente es el
que marca la diferencia. En efecto, el cálculo de avance de un proyecto $\mathit{AP}$ se
realiza sobre el estado sus hitos: N°de Hitos finalizados/N°de Total Hitos
$(1)$. Donde no se toma en cuenta ni calendarios, Carta Gantt o cronogramas,
puntos de control, agendas, etc.
Ciertamente el Control y Seguimiento de Proyectos es más complejo que este útil
y naïve enfoque numérico. (Ver
PMO ¿Por qué y cómo?)
Es decir, aquí se aborda la métrica sin considerar una medición en la
administración tareas como los atrasos en entregables, en compromisos,
replanificaciones, aprobaciones o rechazos, reclamos,
comunicación, etc. Los cuales, efectivamente ocurren sobre la finalización
de un hito, durante el proceso de ejecución del proyecto.
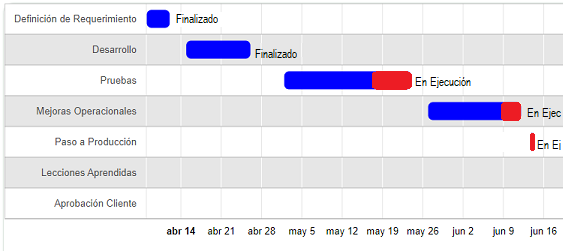Figura #4: Hitos Finalizados ó En
Ejecución
Nótese que un hito debe ser un tramo importante y claro en el encadenamiento de
un proyecto. Es claro que la acción de un evento que tiene una fecha inicial,
una fecha final, un responsable y que juega un rol ineludible en la concreción
del ciclo del proyecto es un hito.
Es necesario remarcar este concepto, dado que el número de hitos, - inserto
dentro de los límites de un subproyecto-, es un denominador en las expresiones
$(1)$ y $(2)$, donde su magnitud tiene un efecto
directo en esas formulaciones. Esto implica por ejemplo, que si esta cifra es
aumentada por hitos no relevantes, - de fácil término que no marcan un cambio
significativo -, distorsionarán el indicador de Avance del Proyecto.
|
|
