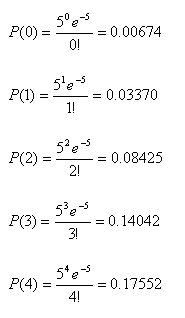|
||||||||||||||||||||||||||||||
|
La cola es un problema de equilibrio entre la oferta y la demanda de servicios. En efecto, las colas de espera se producen por una simple razón: un desbalance transitorio entre oferta y demanda.
Of(t) < De(t) (1) Sin embargo, desde el punto de vista de la gestión de operaciones, la situación es más compleja: ¿Cómo gestionar eficientemente la oferta, y al mismo tiempo satisfacer la demanda ofreciendo una buena calidad de servicio? La gestión de la oferta, o capacidad, de un operador de servicios involucra distintos planos de alcance: el operativo-estratégico, donde se realiza el dimensionamiento de capacidad de largo plazo (por ejemplo, ¿cuántos recursos (o niveles de atención diferenciados) van a implantar en cada sucursal?), y el operativo de corto plazo (¿cuántos de esos roles y recursos deberían estar prestando servicios en un momento dado?). La gestión diaria de los tiempos de espera se centra en este segundo plano. Para configurar un sistema estable, se debe rotar la inecuación (1). Es decir, lograr que la capacidad ofrecida sea superior (o al menos igual) a la demanda.
De(t) < Of(t) (2)
Preguntas que debe responder el sistema: Un sistema altamente utilizado como son los servicios de atención que se desea prestar a través del mesón, a menos que diversifique su oferta en varios niveles de atención y en suficientes servidores (asistentes), se arriesga a brindar una mala calidad de servicio: largas colas, altos tiempos de espera y, por consiguiente, insatisfacción de los clientes.
Por tanto, en un entorno de sistema congestionado y de baja calidad de servicio, ampliar y/o gestionar adecuadamente la capacidad de la oferta en determinados momentos, es la clave para mejorar su desempeño. Entonces:
¿Cómo lograr en los momentos requeridos tener la oferta de servicio que se requiere? ¿Cómo manejar con eficiencia las colas de espera? ¿Cuántos recursos habría que tener disponibles
en un instante dado? Solución Propuesta Según el análisis realizado, hay dos direcciones entonces sobre las cuales debe trabajar el Banco para mejorar la calidad del servicio. Por un lado, inducir en el cliente expectativas que puedan ser cumplibles; por el otro, gestionar la percepción de los tiempos de espera. La ecuación anterior es netamente dinámica, y se resuelve ante cada encuentro entre el servicio de atención y cliente, en forma consistente a lo largo del tiempo. La propuesta de diseño funcional de DocIRS, para montar un servicio computarizado se basa en dos pilares fundamentales:
i) Transformar, el tiempo de espera en la cola en un tiempo disponible del cliente, mediante atención programada. (Cola aleatoria rápida en el mesón o anfitrión y derivación programada para la atención y entrega final del servicio).
ii) Registro y análisis estadístico dinámico de todos los tiempos controlables, desagregados por servicio, sucursal, mes, día, rol de modo localizar la oferta de servicios en los lugares y momentos oportunos.
De(t-1) < Of(t) (3)
La expresión (3) indica que al conocer en forma empírica, dentro de una muestra de tamaño significativo y diferenciado por sucursal, por día, por horas pick, por servicios, por tiempos de atención, por tipo de recursos (Demanda en tiempo t-1), será posible anticipar la oferta en el tiempo t.[1] Es claro que si se agregan los recursos apropiados aumentando la oferta de servicios en los lugares y momentos de concentración de flujos, los tiempos de espera se reducirán. Un concepto fundamental en la gestión de tiempos de espera es el coeficiente de utilización, definido como el cociente entre demanda promedio, y capacidad promedio ofrecida: r = l/m (4) Por tanto: r: Coeficiente de utilización[2] l: Demanda promedio o tasa de llegada de clientes; m: Capacidad promedio ofrecida o tasa de atención
Se dice que un sistema estable requiere que el coeficiente de utilización r <1 De otro modo se satura y la cola comienza a crecer explosivamente. Medidas de rendimiento:
· Número medio de clientes en el sistema, notado Ls · Tiempo medio de espera de los clientes en el sistema, Ws · Número medio de clientes en la cola, Lq · Tiempo medio de espera en cola de los clientes, Wq
Suponiendo que el sistema no se satura, se deduce la siguiente fórmula para las probabilidades Pn de que haya n clientes en el sistema, donde nÎN:
Pn = rn (1-r) (5)
Probabilidad de que la línea exceda a n:
P(Ls>n) =rn+1 (6)
El número medio de clientes en el sistema, Ls, se calcula así:
En síntesis, sean l= tasa promedio de llegada. µ = tasa promedio de servicio.
De donde se deduce la siguiente Tabla de Medidas que utilizaremos en el modelo: (Ver detalles de la deducción de fórmulas en capítulo Modelo Matemático del Anfitrión).
Tabla de medidas de rendimiento para el modelo de cola
Ejemplo 1:
Supónganos una sucursal donde los clientes llegan para solicitar uno o más servicios con una tasa de 30 clientes por hora y que la capacidad de atención promedio es de 35 clientes por hora.
El modelo propuesto, supone un anfitrión y/o Rol1, que intercambia con dos líneas, y puede tratar este problema de demanda – suponemos que en la realidad - es aun más rápido, dado que esta sola línea distribuirá su oferta en forma programada con los otros dos servidores(Rol2 y Rol3).
Calculando las medidas formuladas en la Tabla de Medidas de Cola
Dados:
l= 30 (tasa promedio de llegada.) µ = 35 (tasa promedio de servicio.)
Utilización de la instalación: r =l/m (r = 30/35=0,857 < 1 condiciones de no saturación) Entonces : Lq=l2/ µ (µ - l) =5,14 clientes (Nº de clientes en la cola para se atendidos)
Wq = Lq/l = l/ µ (µ - l)= 0,17 hora, equivalente a »10 minutos de espera en cola
Ls = Lq + l/ µ = l/ (µ - l) = 6 clientes en espera dentro del sistema.
Ws = Ls/l = 1/ (µ - l)= 0,2 hora, equivalente a 12 minutos dentro del sistema
P(Ls>6) = rn+1=r6= 0,339916677 probabilidad de que la cola exceda a 6 clientes
Conclusión: Por tanto, para este ejemplo, el cliente promedio espera 10 minutos antes de ser servido. En promedio, hay un poco más de 5 clientes en la línea o 6 en el sistema. El proceso completo lleva un promedio de 12 minutos. El anfitrión está ocupada alrededor del 86% del tiempo. Y finalmente, el 34 % del tiempo habrá 6 personas o más en el sistema (o 5 o más esperando en la cola).
Cálculo de la probabilidad de la cola mediante la distribución de
Poisson. Al usar la distribución de Poisson en nuestro modelo, según hemos señalado, describiremos el proceso de las colas del mesón con una variable aleatoria discreta. Sea n Î N* la variable aleatoria que representa el número de clientes en la cola. Es decir, n puede asumir valores enteros {0,1,2,3 ..} La probabilidad de exactamente n ocurrencias en una distribución de Poisson se calcula mediante la fórmula:
Donde
l
es la tasa de ocurrencias (en nuestro caso puede se de llegada o de
servicio) o promedio de clientes por unidad de tiempo. Ejemplo 2: Desde las matrices de datos que se capturan por el Sistema de Atención de Clientes, se indica una media de llegada de 5 clientes cada 10 minutos (l=5) durante el primer día miércoles de cada mes. Asumiendo que el número de clientes ingresando a la cola está distribuido conforme a la distribución de Poisson, proyectaremos a partir de la evidencia empírica del sistema, la probabilidad de que 0,1,2,3 y 4 clientes formen la cola en un intervalo entre las 11:50 y las 12:00 del primer miércoles de un mes determinado.
∑---------------------- P(n≤4)= 0.4063
Modelo Matemático del anfitrión[3] Las llegadas al mesón son aleatorias, puesto que son independientes entre sí La experiencia histórica en tratamiento de colas, ha determinado que las ocurrencias aleatorias de un tipo especial pueden describirse a través de la distribución discreta de probabilidad de Poisson. Este tipo especial de llegadas aleatorias supone características acerca de los flujos de entrada. En primer lugar, se supone que las llegadas son por completo independientes entre sí y con respecto al estado del sistema. En segundo lugar la probabilidad de llegada durante un periodo específico no depende de cuando ocurre el periodo, sino más bien, depende solo de la longitud del intervalo. Se dicen que estas ocurrencias carecen de "memoria". Si conocemos el número promedio de ocurrencias por periodo, podemos calcular las probabilidades acerca del número de eventos que ocurrirán en un periodo determinado, utilizando las probabilidades conocidas de la distribución de Poisson. (Ver expresión (8))
Tiempo de servicio aleatorio (M / M / 1) Al igual que las llegadas aleatorias, la ocurrencia de tiempos de servicios aleatorios, carentes de memoria, es suceso bastante común en las situaciones cotidianas de líneas de espera. Y al igual que las llegadas aleatorias los tiempos de servicio carentes de memoria se describen a través de una distribución de probabilidad. La diferencia entre las llegadas aleatorias y los tiempos de servicio aleatorios es que estos se describen a través de una distribución continua en tanto que las llegadas se describen a través de una distribución de Poisson, que es discreta. Si la duración de los tiempos de servicio es aleatoria, la distribución exponencial negativa describe ese tipo de servicio. Si la μ es la tasa promedio de servicio entonces la distribución esta dada por: F(t) = μ e-μ t Es posible emplear esta formula para calcular la probabilidad de que el servicio sea mas prolongado que alguna duración especificada de tiempo T. En la siguiente figura se representa es modelo. Características de operación Para calcular las características de operación de una cola M / M / 1, primero debemos de observar que sí l = tasa promedio de llegadas y μ = tasa promedio de servicio, entonces l debe de ser menor que μ . Si esto no ocurriera el promedio de llegadas sería superior al número promedio que se atienden y el número de unidades que están esperando se volvería infinitamente grande. Si hacemos que r = l / μ puede denominarse a r como factor de utilización. Este valor es la fracción promedio de que el sistema este ocupado, también sería el número promedio de unidades que están siendo atendidas en cualquier momento. En términos de probabilidad tendríamos que: Pw = probabilidad de que el sistema esté ocupado. (Ver expresión (4)) Pw = r = l/m Entonces la probabilidad de que el sistema no esté trabajando, o esté vacío, P0, puede obtenerse por medio de:
A partir de esto podemos obtener la probabilidad de que haya n unidades en el sistema, Pn, mediante: En donde n es cualquier entero no negativo. Este importante resultado nos permite calcular las características de operación de las líneas de espera. La primera característica de operación que calculamos es el numero promedio de unidades que se encuentran en el sistema, ya sea esperando o siendo atendidas. Denominaremos a este número promedio de unidades promedio, Ls. Entonces tenemos que:
Con estos valores obtenidos podemos calcular el número promedio de unidades que esperan ser atendidas, Lq. Dado que L es el número de unidades que están esperando o están siendo atendidas, y r es el número promedio de unidades que están siendo atendidas en algún momento dado entonces: Ls = Lq + r A partir de esto es fácil observar que Lq = Ls - r O también podríamos decir que
Ahora examinaremos el tiempo de espera. Utilizaremos Ws para representar el tiempo promedio o esperado que una unidad se encuentra en el sistema. Para encontrar Ws, observaremos que es Ls el número esperado de unidades en el sistema y l es el número promedio de unidades que llegan para ser atendidas por periodo, entonces el tiempo promedio de cualquier unidad que llega debe estar en el sistema está dado por: Ws = tiempo promedio de una unidad en el sistema
De manera similar, el tiempo esperado o promedio que una unidad tiene que esperar antes de ser atendida, Wq, esta dado por:
[1] Nótese que existen determinados días del mes y horas que se produce mayor demanda sobre ciertos servicios, que el administrador de la sucursal puede anticipar localizando los recursos precisos para generar la oferta que estabilice el sistema manteniendo la calidad de servicio. [2] Este parámetro r también es llamado carga, flujo o intensidad de tráfico del sistema, puesto que mide la relación entre la cantidad de trabajos que llegan y la capacidad de procesarlos [3] Llegadas aleatorias (M / M / 1).Este sistema trata de una distribución de llegada Markoviano, tiempo de servicio Markoviano, y un anfitrión.
|