
Puertas Lógicas Clásicas y Cuánticas ~ Circuitos Cuánticos

José Enrique González Cornejo
v.7.6/Marzo 2020
|
Puertas Lógicas Clásicas
Para manejar la información almacenada en un conjunto de bits, utilizamos las
llamadas Puertas Lógicas, que se basan el Algebra de Bool o Lógica Proposicional
con tres conectivas básicas y sus variantes: ~p, p ∨ q, p ∧ q, p ⇒ q, p ⇔ q, (p
⇒ q) ⇔ (~p ∨ q), etc.. junto a las Leyes de Morgan.
Puerta AND
Puerta OR
Puerta NAND Existe una puerta lógica NAND, que es particularmente importante en computación, la cual es una composición de AND con NOT. Esta conectiva tiene una propiedad de universalidad24 y es muy utilizada en la programación. En efecto, cualquier circuito lógico clásico se puede hacer con una concatenación de puertas NAND.
Ejemplo de Suma de $1+1+1$ con Computación Clásica con Bits
La idea del ejemplo es explicar lo más detalladamente posible el desarrollo de
esta suma con computación clásica, con el objeto de ir preparando en forma
preliminar el algoritmo 1+1+1 con qubits, que
ilustraremos más adelante con el Composer Cuántico de IBM. En este ejercicio de
computación clásica se utiliza un operador de Thomas Toffoli, que en los años 80
junto a Edward Fredkin descubrieron que se requería un mínimo de tres qubits, -
para cualquier computación clásica-, a fin conservar la Reversibilidad.

Tabla Suma 1+1+1 con con Bits Explicación de Suma de $1+1+1$ con Bits
Algoritmo-Interfaz Suma Números Binarios
Sumar números binarios es semejante a la operación simple que se aprendió en la
escuela con números decimales, pero la Suma es Modulo $2$.
Nótese que $1⊕1=0$ y se reserva $1$, el cual se adiciona a la siguiente posición. En caso de que quede en una posicion o columna la suma de 3 unos ($1 ⊕1 ⊕1=1$), entonces se reserva $1$ para la siguiente posición, y así sucesivamente.
Esta operación clásica que se aplica en cuántica (Ver más adelante
Circuito Suma Toffoli-CNOT), donde se muestran las pautas para sumar
simultáneamente con una única unidad de control.
El camino hacia la construcción consolidada de una computadora u ordenador
cuántico proviene del hecho de que algunos algoritmos funcionan
significativamente y más eficazmente en una computadora cuántica que en una
computadora clásica.26
 Estados Básicos y Estado en Superposición. Ambos son Estados Únicos.
A fin manejar la información almacenada en un conjunto de qubits y extraer
información útil utilizando la interferencia cuántica, utilizamos Puertas
Cuánticas. La definición de una puerta cuántica requiere conocer su efecto sobre
los estados básicos y se necesita saber también cómo se comporta con una
combinación lineal. Las leyes de la mecánica cuántica nos dicen que la evolución de un sistema responde a la Ecuación de Schrödinger29 (si no se realiza una medida). Se reitera que en el presente artículo sólo está enfocado en la matemática computacional y no en la física cuántica que es la fuente experimental de donde derivan la mayoría de los postulados que iremos mostrando a los largo de los capítulos y versiones del documento. En síntesis para definir una Puerta Cuántica y es necesario que una matriz para:
Ejemplo de Matriz Unitaria Demostrar que la matriz $A$ es Unitaria.
$∴\quad A$ es una matriz Unitaria, dado que $A^{t}=A^{*}$, donde $AA^{*} = A^{*}A = I$. Es decir, la matriz conjugada es la inversa, $A^{*} = A^{-1}$. Por demostrar que $A^{*}=A^{-1}$
QED. Puertas Lógicas Cuánticas
Una Puerta Lógica Cuántica es un circuito cuántico básico que opera sobre un
pequeño número de qubits. El concepto y construcción de puertas cuánticas es
innumerable, dado que pueden ser composiciones que se configuran con operaciones
simples. Estas puertas se representan con matrices unitarias que actúan sobre
las amplitudes de probabilidad de los qubits. Pero las puertas primitivas o que
se denominan universales, - ver IBM Experiencia Cuántica Editor de IBM QX -, son
matrices 2×2 que cumplen con todas las condiciones antes especificadas
previamente.
En la Ayuda en línea del Composer de IBM, se describen gráficamente las puertas
lógicas cuánticas simples (Por ejemplo las de Pauli y los operadores matriciales
$U_n$ y otros), utilizando la Esfera de Bloch. Esta representación es un
herramienta de visualización importante para comprender lo que sucede con un
circuito cuántico.
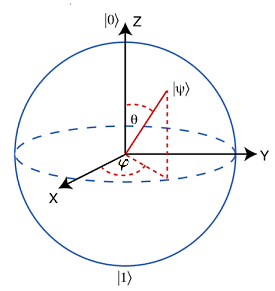 Esfera de Bloch. Fuente: IBM Quantum Experience
La Esfera de Bloch, se utiliza con el fin didáctico para comprender la variación
del qubit, - restringido sólo como objeto tridimensional-, bajo la aplicación de
los operadores.
$$|\psi〉=cos(\frac {\theta}{2})|0〉+(\cos\theta+ i\ \sin \ φ)\sin(\frac
{\theta}{2})|1〉$$
A continuación las cuatro matrices de Pauli31,
X, Y, Z.
i) $|0〉 → |1〉$ y $|1〉 → |0〉$
La puerta de Hadamard es muy importante y consecuentemente utilizada en
los algoritmos de la computación cuántica, por que se presta para ir
aprovechando las ventajas de manejo de la evolución de los estados en
superposición, hasta llegar a un lugar que medir esa superposición sea útil para
contribuir a solucionar el problema con el algoritmo en cuestión.
 $H$ ibm quantum experience-fuente gates glossary En general, cuando se comienza a construir un algoritmo cuántico, se establece un conjunto de qubits de inicialización en estado cero, pero se prepara el circuito para introducir los estados en superposición equiprobables con Hadamard. Nótese que la puerta lógica cuántica de Hadamard $H$, se puede expresar como una combinación de las puertas universales de Pauli, $X$ y $Z$. En efecto, $H=\frac{1}{2}(X + Z)$, lo que es facilmente comprobable: $ \large{\frac {1}{\sqrt{2}}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \\ \end{pmatrix} $ = $\large{\frac {1}{\sqrt{2}}}$ $ \Biggl( \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix} $ + $\begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix} \Biggr)$ Ahora, si se aplica el producto tensorial $⊗$ con $H$ sobre vectores de varios qubits (operador de Walsh-Hadamard), utilizando la notación en $n$, descrita previamente en Modo Numérico de Representar los Vectores Unitarios. Este producto tensorial con Hamadard, se describe mediante la siguiente expresión: $$H ⊗ H ⊗ H ⊗\cdots H |\underbrace{0 0 0\cdots 0}_{n\text{ veces}}〉=\frac {1}{\sqrt{2^{n}}}\sum_{x=0}^{2n-1} |x〉$$ Por ejemplo, con $n=2$: $$H ⊗ H |00〉=\frac {1}{\sqrt{2}}(|0〉+|1〉) ⊗ \frac {1}{\sqrt{2}}(|0〉+|1〉)=$$ $$\frac{1}{2}(|00〉+|01〉+|10〉+|11〉=$$
La Puerta cuántica $CNOT$ es una puerta no controlada. Las puertas controladas operan sobre 2 qúbits o más. En este caso su efecto es: Para el Algoritmo de Deutsch, es clave comprender la importancia del operador controlado $CNOT$ (denotado como $CX$ en el Composer Quantum de IBM), que se aplica con al menos $2$ qubits.  $CNOT$ ibm quantum experience-fuente gates glossary A diferencia de las Puertas de Pauli, - descritas previamente -, las cuales son transformaciones unitarias, i.e. de un qubit y pueden ser representadas en sus dos estados por su rotación en los ejes de la Esfera de Bloch. Así mismo, la puerta de Hadamard, - que rota sobre el eje de las ordenadas $Y$ -, juega un rol preponderante de superposición en el Algoritmo de Deutsch. Nótese que si el qubit de control del operador $CNOT$ está en un estado de superposición, se crearán entrelazamientos (Ver Estado de Bell). En efecto, la transformación $CNOT$ es una puerta de $2$ qubits de entrada. Se ilustra a continuación:
El primer qubit $x$ se llama control. El control es invariante en la transformación. El segundo qubit $y$ se llama objetivo. El objetivo se niega cuando $x$ = $1$. Es decir, $y$ no cambia si $x$ = $0$. La operación $⊕$ es la conectiva ∨ (XOR) que corresponde al OR excluyente en el Algebra de Boole. La operación $⊕$ se utiliza como la llamada suma módulo $2$. Es decir, el primer bit de entrada $x$ siempre se pasa directamente; el segundo bit se aplica sí y solo sí el bit de "control" $x$ es $|1〉$, i.e. aplica un Pauli $X$ en el objetivo. Para ser aún más explícito, $CNOT$ tiene la siguiente tabla de verdad:
Para explicar paso a paso la Matriz $CNOT$, Consideremos los vectores de base $|0〉$ y $|1〉$. Apliquemos a cada columna la operación $CNOT$ antes definida y veremos que las dos primeras columnas permanecen invariantes por que el qubit de control es $0$, y las dos últimas columnas cambian porque el qubits de control es $1$, obteniendo la siguiente matriz: $$ CNOT= \begin{pmatrix} 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ \end{pmatrix} $$
Puerta de Toffoli
La puerta de Toffoli cubre la necesidad de tener un mínimo de tres qubits para
cualquier computación clásica. La extensión a tres qubits de la puerta CNOT se
denota como CCNOT o también Puerta de Toffoli (En el "Composer de IBM", el
objeto se denomina CX). Para eso, se definen dos bits de control que sólo actúan
si están a $1$. Al aplicarla dos veces resulta la identidad. Por tanto, es una
puerta reversible (su inversa es ella misma). La expresión matricial es:
La puerta clásica de Toffoli es una transformación de 3-qubits que cambia el tercer qubit, cuando los dos primeros son $1$. Evidentemente es una transformación unitaria. La puerta de Toffoli, es de gran utilidad en el diseño de algoritmos cuánticos, permite equipararlos con algoritmos de computación clásica, ya que es universal para la computación booleana. Más adelante se utilizará en los ejemplos con el Editor Composer de IBM, también en forma extendida atravesando más cables (o qubits) y con puertas equivalentes como $U_3$32. Su representación es el siguiente diagrama: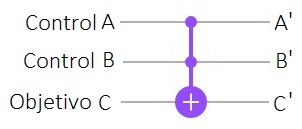 Diagrama Puerta Toffoli o CCNOT  Tabla Síntesis con Entradas y Salidas Toffoli
A fin de manipular recursos "algebraicos" en la construcción de algunos
circuitos cuánticos es necesario introducir puertas lógicas cuánticas ternarias.
Toffoli es una de ellas, dado que es una puerta NOT con dos controles previos al
objetivo.
Si se observa, tanto la representación matricial como la Tabla de Entradas y
Salidas de la Puerta de Toffoli, se determinará que la resultante $C^{'}$,
obtenida mediante operaciones booleanas, se expresará con la siguiente
proposición lógica:
Ahora, que ya se describieron las puertas cuánticas elementales, se complementa lo tratado en previamente en Algoritmo - Interfaz Suma Números Binarios, a fin de ir introduciendo un simple circuito cuántico para las sumas de dos bits. Utilizando las Puerta de Toffoli y CNOT, - donde las entradas $x, y \in${$0,1$} -, con el tercer qubit en cero. Se ilustra el siguiente diagrama: 
Circuito Cuántico ~ Suma Toffoli y CNOT
Son concatenaciones de puertas cuánticas o una sucesión de modificaciones de un
conjunto de qubits, que producen consecutivos cambios de estado en un ordenador.
Esta notación gráfica de diagramas, se expresa mediante cables horizontales (uno
por qubits) sobre los cuales se localizan las puertas cuánticas. Se leen de
izquierda a derecha. A continuación una imagen animada de ejemplo extraído de
"IBM Q, Introduction to Quantum Circuits, Getting started with quantum circuits
URL:
https://quantum-computing.ibm.com/".
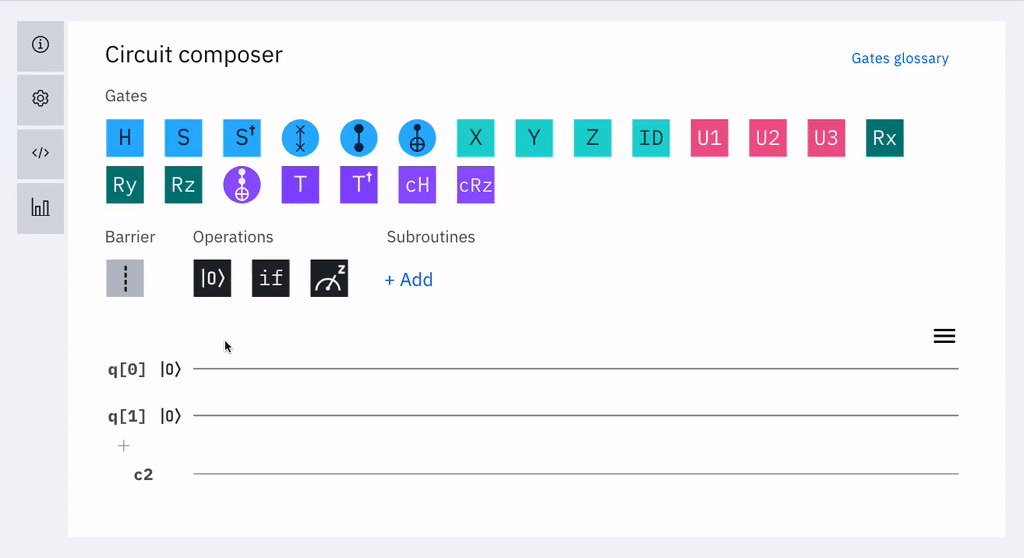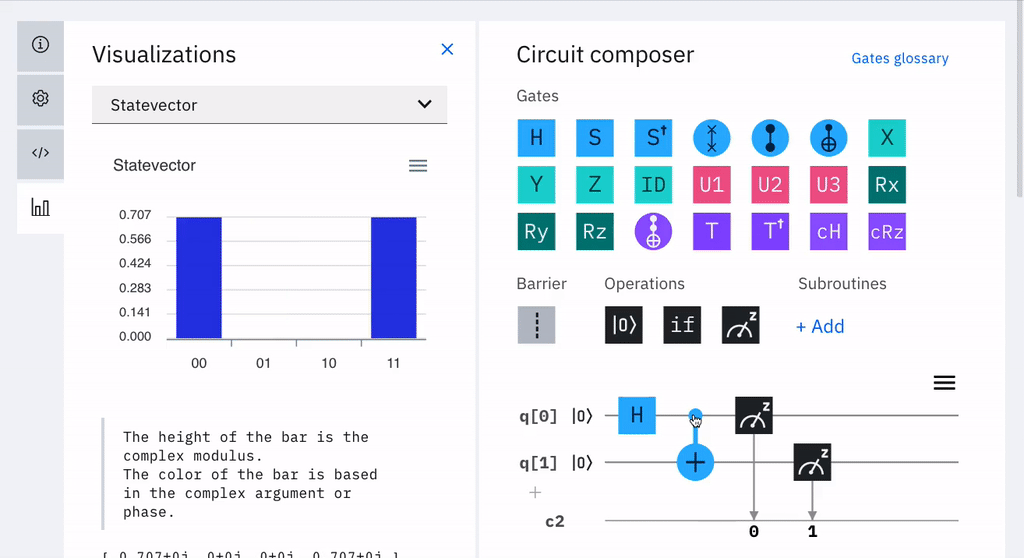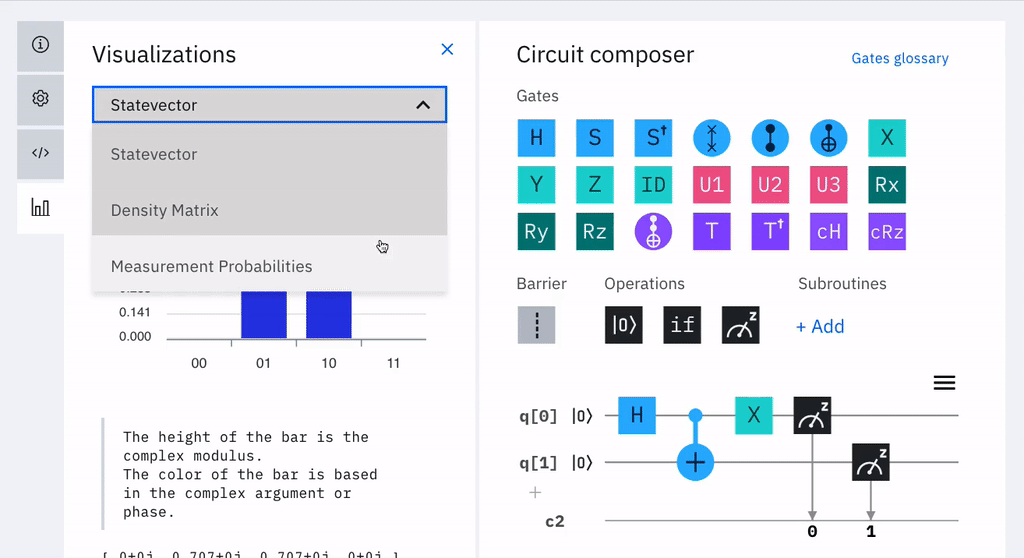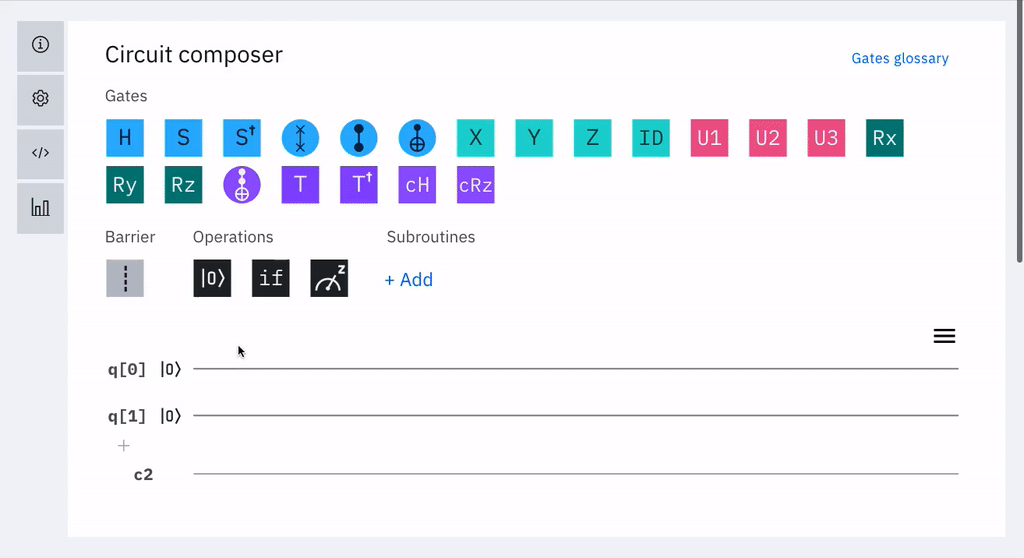
Vista Principal del Editor Circuit Composer de IBM En un siguiente ejercicio se construirá el algoritmo que calcula 1+1+1, describiremos detalladamente paso a paso el cicuito cuántico utilizando el Composer de IBM. Nótese que generalmente los qubits de los algoritmos se inicializan en cero. La notación q[0],q[1],..q[n] para descomponer los qubits. Por ejemplo: |001〉 se presenta como q[0]=0, q[1]=0 y q[2]=1.(Revisar operador Barrier33)  Circuito Algoritmo 1+1+1 con el Editor de IBM  Ver
Video Ver
Video
Los Estados de Bell son cuatro específicos estados cuánticos máximamente
entrelazados de dos qubits. Están en una superposición de $|0〉$ y $|1〉$ , i.e.
en una combinación lineal de estos dos estados.
 Descripción de los Pasos del Circuito Los pasos aplicados en este circuito cuántico para crear un estado de Bell son los siguientes: 1.- La puerta de Hadamard transforma el primer qubit q[0] a un estado de dos qubits: $${(|0〉+|1〉)|0〉\over \sqrt{2}}{={(|00〉+|10〉)\over \sqrt{2}}}$$ 2.- A continuación, a ese resultado se le aplica el CNOT: $${(|0\ \ 0⊕0〉 + |1 \ \ 0⊕1〉)\over\sqrt{2} }$$ 3.- Por lo tanto se obtiene: $${(|00〉+|11〉)\over\sqrt{2} }$$  Circuito con el Editor de IBM  $$|00〉\rightarrow \frac {1}{\sqrt{2}}(|00〉+|11〉)\rightarrow \frac {1}{\sqrt{2}}(|00〉+|11〉) \rightarrow \frac {1}{\sqrt{2}}(|00〉-|11〉)$$ El mismo circuito con el Editor de IBM se obtiene el siguiente resultado: 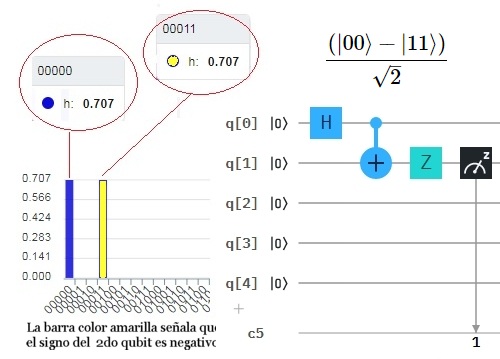 Circuito con el Editor de IBM Ejemplo de Indempotencia34 con CNOT Dado el siguiente diagrama de Puertas Cuánticas. ¿Cuál es el resultado? Resultado:  Dos puertas Hadamard en serie resultan en un qubit con el estado original.  H H H H |ψ〉 |ψ〉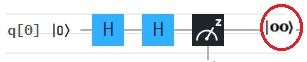 Se puede ver claramente que este mapeo es una biyección 35, lo que confirma que CNOT es una puerta reversible. (Ver una generalización pequeña pero importante, llamada CCNOT (control controlado-NO) o Puerta Toffoli.) Ejemplo de Algoritmo con Puertas de Pauli
Construir un algoritmo que transforme un qubit en estado |0〉 a un estado
-|0〉   Circuito con el Editor de IBM |
|
Notas Complementarias Adjuntas
|
Puertas Lógicas Clásicas y Cuánticas ~ Circuitos Cuánticos
| DocIRS © 1988-2026 |