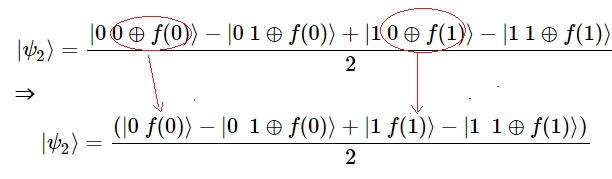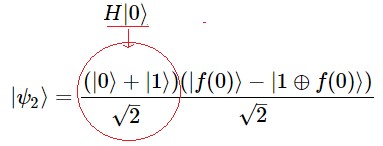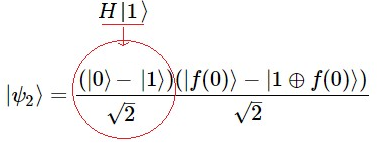Conceptos Matemáticos Básicos de Computación Cuántica
José Enrique González Cornejo
v.9.2/Marzo 2020 ~ Upgrade 12/05/2021
|
+ Mapa Publicaciones |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| + Videos Asociados |
|
+ Introducción |
|
+ Esquema del Contenido |
|
+ Preguntas Implícitas |
|
+ Estructura y Uso |
|
+ Indice Completo Desplegado |
|
I. Computación Clásica versus Computación Cuántica
Inicialmente mostraré cómo computación clásica utiliza el almacenamiento de datos basado en dispositivos digitales que almacenan "bits", los cuales son binarios ($0 \text{ o } 1$). Es decir, en sólo en dos estados distintos en un momento determinado, mientras que las computadoras cuánticas utilizan propiedades de la mecánica cuántica, tales como la superposición y el entrelazamiento cuántico.
El bit (Binary Digit) es la unidad mínima de información empleada en informática, que se expresa por dos posibles estados $0$ y $1$. Con esta base binaria se hace uso directo del almacenamiento primario de datos. 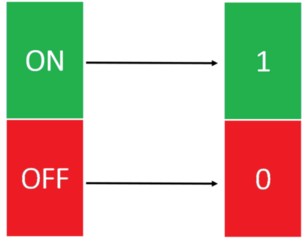
Representación Bit: Binary Digit
Es muy importante en esta comparación tener presente, que en el estado que está el bit es el estado que observamos del bit. 
Representación Almacenamiento de Numeración Binaria Sobre esta unidad básica de información, llamada bit se basa la computación clásica. A continuación se ilustra una interfaz, - que contiene un algoritmo-, que transforma números decimales a su equivalente binario. (Ver Algoritmo para el Cambio de Base Numérica) |
| Decimal | Base | ||
Ingrese Número |
|||
| Entero Decimal | Equivalente Base | |||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
La unidad básica de la información cuántica es el qubit55. Un qubit corresponde a un sistema físico que
tiene dos estados ortogonales, que denotamos de acuerdo a la Notación de Dirac1 como:
$|0〉$ y $|1〉$. Los estados del sistema, que denotamos $|ψ〉$ se denominan kets.
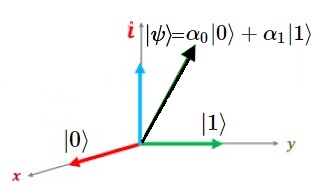 Dirac: Representación de Estados Ortogonales
Estos estados no vacíos se tratan como vectores de base2. Es decir, se aplica una correspondencia hacia una estructura algebraica de Espacio Vectorial.
Espacio Vectorial - Notación Dirac Los qubits se tratan dentro de un Espacio Vectorial Complejo3 y se determina que por las clásicas 8 propiedades fundamentales:
Superposición
Por tanto, un qubit puede también encontrarse en una Superposición de los estados $|1〉$ y $|0〉$. Es decir, como una combinación lineal de los vectores de base, de la forma:
$\alpha_0|0〉+\alpha_1|1〉$. Estos coeficientes $α_i$, son denominados amplitud de probabilidad4, los cuales son números complejos que se utilizan para describir el comportamiento del sistema. La suma del cuadrado de cada uno de esos módulos,- ($|α_0|^{2} + |α_1|^{2} = 1$) -, representa una probabilidad o densidad de probabilidad. Es decir, estos coeficientes $α_i$ son de la forma $z = x + iy$, donde $i = \sqrt{-1}$.
 Representación de un Atomo sin Medirlo Esta unidad básica de información cuántica que se denomina qubit, se verá de similar a un bit, pero a medida que avanzamos veremos que son fundamentalmente diferentes y que esta diferencia permitirá hacer un procesamiento de información nuevo y muchísimo más potente. Por ejemplo, se probó que dada una función $f(x)$, un algoritmo cuántico es capaz de evaluar la función en múltiples valores de x simultáneamente. (Esto no es posible en el sistema tradicional con bits. Ver Desarrollo Algoritmo de Deutsch más adelante). Desde ya la diferencia con el bit en cuanto al almacenamiento es enorme5, dado que el estado de un qubit en Mecánica Cuántica representa niveles de energía de una partícula subatómica y por tanto su almacenamiento físico es en un dispositivo atómico, el cual permite utilizar los múltiples estados en forma simultánea. Es ahí entonces, donde se van guardando los estados intermedios que adquiere el qubit. De igual modo, la capacidad de ambas unidades básicas de información independientemente de la velocidad, son cuantitativamente diferentes. En efecto, el número de estados que se alcanza al introducir un qubit es exponencial, a diferencia de los estados que se alcanza al introducir un bit. En computación clásica se trabaja con $n$ bits y si se aumenta en un bit, el cambio es a $n+1$ estados de almacenamiento. Es decir, la capacidad de medición física del bit es lineal. 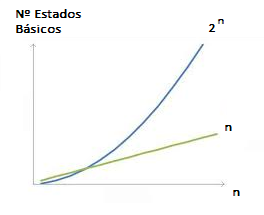
Comportamiento Lineal vs Exponencial En contraste, en un sistema cuántico si se trabaja con $n$ qubits, al aumentar en $1$ qubit se duplica la información que almacena el estado interno ($2·2^{n} = 2 ^{n+1}$). Es decir, el incremento del número de qubits tiene un efecto de medición física exponencial sobre el número de estados o vectores. Sin contar con los estados en superposición del qubit, que pueden ser infinitos. Un qubit está sometido a una variabilidad continua dentro del conjunto de estados cuánticos. Al medir ese estado en movimiento, el sistema determinísticamente asume un estado único. Es decir, el proceso de medición le produce un colapso al estado en superposición y converge a uno de esos estados cuánticos. (Ver Medir una Superposición)  Representación de un Atomo Colapsado (Medido) La relación entre el número de qubits $n \ge 1$ y el número de estados o vectores $m=2^{n}$ define el poder del computador cuántico y la posibilidad de codificar su evolución. Dado que al medir el sistema en superposición, se tiene un número exponencial de estados determinísticos, donde el sistema, - bajo cierta probabilidad -, colapsará a uno de ellos. Más adelante, se mostrará algebraicamente, que los estados cuánticos de qubits múltiples son un producto tensorial de la base canónica {$|0〉,|1〉$}.(ver Estado de Múltiples Qubits) Por ejemplo con $n=2$ bits, se opera con $2$ estados básicos $|01〉,|10〉$. Mientras que con $n=2$ se cuentan $4$ estados básicos $|00〉,|01〉,|01〉,|11〉$, y con $3$ qubits 8 estados, $4$ qubits 16 estados,...y la serie en potencias de $2$ continúa así sucesivamente. (Ver Eligir Nº Qubits - Simular Amplitudes Aleatoriamente.)
En el párrafo de paralelismo cuántico, - más adelante-, veremos que uno de los efectos más significativos de la aplicación de la superposición cuántica dentro de un algoritmo, justamente se basa en el hecho de poder realizar múltiples operaciones sobre un mismo estado cuántico.
  Maurits Cornelis Escher: Peces y Pájaros Puesto en Superposición sobre Colores
Obviamente, esta propiedad implica un tremendo incremento en la capacidad computacional, dado que se computan secuencias de transformaciones unitarias simultáneas por cada elemento en superposición, generando un procesamiento masivo de datos paralelos.
Nanotecnología, Microelectrónica, Lenguajes conectan al mundo cuántico
Es decir, para darnos una idea tomemos un número aleatorio cualquiera $\alpha \in R ,\quad$ tal que $0 < \alpha < 1$. Entonces la posición del estado básico $|0〉$ tiene la amplitud de probabilidad $\sqrt{\alpha}$ y en la posición del estado básico $|1〉$ la amplitud de probabilidad $\sqrt{1-\alpha}$.
|
||||||||||||||||||||
|
Ejemplo Estado Superposición: Si tenemos el siguiente ket:
y se verifica que $|α_0|^{2} + |α_1|^{2} = 1$, entonces $α_0$ y $α_1$ son amplitudes de probabilidad compleja. De modo que, si $|\alpha_0|^{2}=0.4$ y $|\alpha_1|^{2}=0.6$, esto implica que existe la probabilidad en un 40% de colapsar hacia $|0〉$ y del 60% de que el qubit pudiese colapsar a $|1〉$.
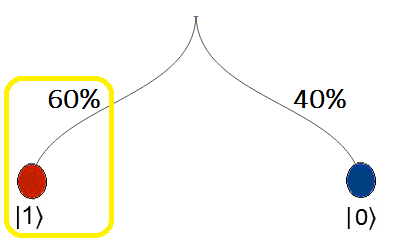
Decimos colapsar, dado que al momento de observar o Medir una superposición8, el sistema sólo permite mostrar uno de los dos estados básicos $|0〉$ o $|1〉$.
Es decir, va a colapsar a uno de los estados básicos dependiendo de la distribución de probabilidad que tenga en ese instante. Considerando que en cada micro-nano-segundo de tiempo, el qubit se encuentra en una superposición de estos estados.
|
||||||||||||||||||||
 |
← | ||
|
Mientras gira la moneda no es posible determinar el estado en que se encuentra.  Infinitos Estados en Superposición
En computación cuántica el sistema puede ser manipulable en su evolución12. Sin embargo, existe un obstáculo aun hoy, en cuanto al almacenamiento. El problema de los estados cuánticos que forman los qubits es que son muy frágiles, y colapsan en cuestión de nanosegundos.
13
$$\psi = \sum_{i=0}^{n-1} u_i |i〉\qquad\qquad [1]$$ $$\sum_{i=0}^{n-1} |u_i^{2}| = 1 \qquad\qquad [2]$$ |
|
Estado de Múltiples Qubits
La notación de Dirac incluye una operación llamada producto tensorial, denotada como $⊗$. Esto es importante porque en la computación cuántica, un vector de múltiples qubits, es posible descomponerlo como producto tensorial de los dos vectores de estado básico (Ver Estado Producto).
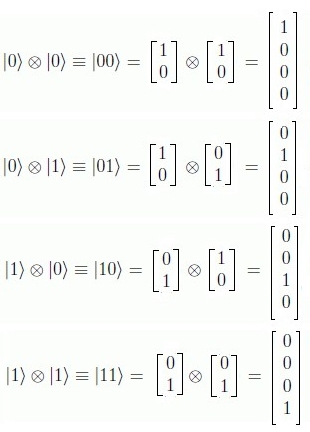 Si definimos dos espacios complejos de dimensión finita $V$ y $W$ de dimensiones $n$ y $m$ respectivamente, en el espacio de Hilbert, con sus bases ortonormales: {$v_i$}$_{i=0}^{n-1}\quad$ y $\quad${$w_j$}$_{j=0}^{m-1}$
Entonces el producto tensorial entre $V⊗W$, es un espacio que tiene como base:
$\Rightarrow$ $$Dim(V⊗W)=Dim(V)⊗Dim(W)$$ Atención por que existen vectores en el espacio complejo unitario que no se pueden expresar como producto tensorial de estados básicos. Estos estados se dicen que están entrelazados.(Ver más adelante Estado de Entrelazamiento Cuántico)
En efecto, podemos extender la notación a varios qubits y configurar matemáticamente un sistema cuántico. A continuación se verá que cuando se trata de múltiples qubits, el número de vectores o de estados que se incorporan a la combinación lineal. Si $n$ es el número de qubits entonces los estados que se generan son $2^{n}$, dado que responde a la cantidad de combinaciones que se configuran con los estados básicos {$|0〉, |1〉$}.
|
|
|
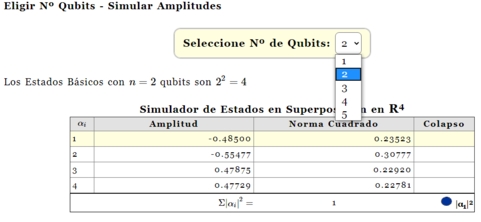
Eligir Nº Qubits - Simular Amplitudes Aleatoriamente15
El simulador permite seleccionar el número de qubits (1 a 5), utilizando el listbox. Los cálculos de las amplitudes de probabilidad $\alpha_i$ se van generando dinámicamente. Del mismo modo, más abajo se publica la variación del estado cuántico del ket $|\psi〉$ y el cumplimiento de la regla de densidad de probabilidad ($|α_0|^{2} + |α_1|^{2} = 1$). Al momento de presionar el botón Medir, el sistema va colapsar mostrando el resultado. También admite visualizarlo en una gráfica de barras con la distribución del instante. Para poner en marcha nuevamente el sistema basta con presionar el botón Superponer y continuar probando. |
|
En la simulación antes descrita, se muestra el cálculo, - en forma dinámica-, de los múltiples coeficientes (o amplitudes) de los qubits en los números Reales, a fin de que la suma de sus normas al cuadrado sea igual a $1$.
El algoritmo cuántico va almacenando información de la superposición de los estados que se están generando, los cuales son manipulados mediante transformaciones unitarias. En cierto instante, se colapsa el sistema para extraer información útil del ket $|\psi〉$ resultante.
Mientras más qubits maneje un procesador cuántico, la potencia de cálculo es de magnitud astronómica. Los experimentos de cálculo realizados hasta hoy con estos aparatos, son capaces de manejar y calcular en segundos estimaciones que en un computador normal demoraría 10.000 años.
Ejemplo de normalización con números aleatorios Reales: Tomemos arbitrariamente un conjunto con cuatro valores {$0.34, 0.56 , 0.48, 0.67$} ($α_i$=Math.random). Entonces, 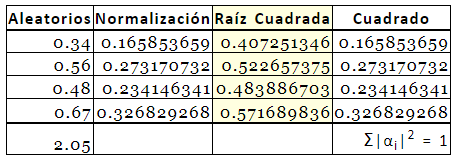
La normalización significa que cada uno de los valores reales aleatorios del conjunto {$0.34, 0.56 , 0.48, 0.67$}, se divide por su suma $Σ|α_i| = 2.05$ (Ver primera columna de la tabla).
Formalizando el ejemplo,(aplicando $[1]$):
Dado un $n∈\mathbb{N}$. Sea $m=2^{n}$, entonces el conjunto $A =${$α_1, α_2, α_3,...., α_m$} de $m$ valores seleccionados aleatoriamente, tal que $Σ|α_i|^{2} = 1$ , donde cada $α_i ∈R$ y $0< α_i< 1$ , con $i = 1,2,3,..m$. Se determina, - en este ejemplo en particular-, con las siguientes funciones en javascript:
Matriz de $\quad 2^{2} \times 2^{2}\quad =\quad$4 $\times$ 4
Coeficientes Complejos
El hecho de que las probabilidades deben sumar uno, pone algunas restricciones sobre lo que pueden ser los coeficientes o amplitudes en la combinación lineal:
Y dado que los cuadrados de estos coeficientes $α$ y $β$ están relacionados con la probabilidad de obtener un resultado de medición, ellos están limitados por el requisito:
De modo que cuando esta condición es satisfactoria para los cuadrados de los coeficientes de un qubit, se dice que el qubit está
normalizado y admite calcular el módulo de estos números de la siguiente manera 16 :
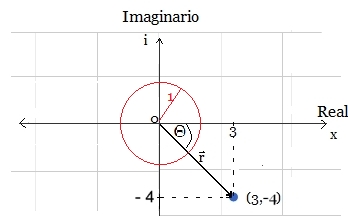
$|β|^{2}=ββ^{*}$ Donde $α^{*}$ es el complejo conjugado de $α$ y $β^{*}$ es el complejo conjugado de $β$. Es decir, si $z = x + iy$ , entonces el conjugado es $z^{*} = x - iy$, donde $x, y \in R$. (La regla práctica para obtener el conjugado $z^{*}$, es cambiar el imaginario $i$ por $-i$) 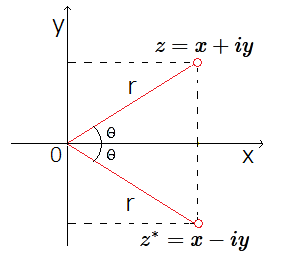 Representación Gráfica de $z$ y $z^{*}$ 17 Por tanto el modulo: |z|2=(x + iy)(x - iy)=x2 + ixy - ixy + y2 $\Rightarrow$ |z|2 =x2 + y2 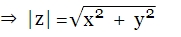
Ejemplos:
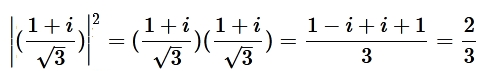 Por tanto, la probabilidad del que el sistema cuántico $|ψ〉$ se encuentre en estado $|0〉$ es $p = \frac {2}{3}$ Obviamente la probabilidad de que $|ψ〉$ se encuentre en estado $|1〉$ es $q = 1 - \frac {2}{3} = \frac {1}{3}$ Función javascript - Normalización
A continuación, el código de una función en javascript para la normalización de un número complejo, ingresado en forma separada su parte real e imaginaria.
Amplitudes de Probabilidad con Números Complejos
En las tablas a continuación se ilustra cómo se normaliza un conjunto de números complejos, a fin de satisfacer el requisito de que la suma de los módulos al cuadrado de las amplitudes de probabilidad de todos los estados posibles es igual a 1.
Nótese que al presionar el botón Medir, colapsa el sistema en el estado básico más probable, de inmediato aparece el botón Superposición que al presionarlo activa la generación de amplitudes de probabilidad dinámicamente y vice versa. Los coeficientes complejos generados dinámicamente en forma aleatoria en la Tabla#1 se normalizan en $u_i$ en la Tabla#2, y permiten representar el estado de un qubit en superposición. En efecto, valores que pueden describir el comportamiento de un sistema cuántico. El cuadrado del módulo de esta cantidad representa una probabilidad o densidad de probabilidad. La cantidad de $2^{n}$ coeficientes generados se realiza en función del número $n$ de qubits que se está operando. En general en programación cuántica, se utilizan amplitudes de probabilidad que son equiprobables. Cuando se configuran circuitos con puertas cuánticas y se ejecutan múltiples veces (que es lo usual), las probabilidades tienden al valor esperado. Es decir, si el número de qubits es $n$, entonces se utilizan uniformemente distribuidos los valores en los coeficientes $α_i=1/\sqrt{n}$. Por ejemplo, la Base de Hadamard (denominada así en honor al matemático francés Jacques Hadamard) en $C^{2}$:
Dada una base ortonormal, cualquier estado puro $|ψ〉$ de los vectores $|0〉$ y $|1〉$ de un sistema cuántico de dos niveles se puede escribir como una superposición de los vectores base, donde el coeficiente o la amplitud de cada vector base es un número complejo. Sin embargo, dado que sólo la fase relativa entre los coeficientes de los dos vectores básicos tiene algún significado físico, podemos tomar el coeficiente de $|0〉$ como real y no negativo.
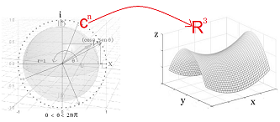
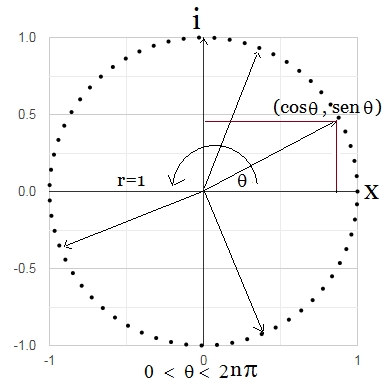
Nótese que al normalizar un número complejo $z$ en su forma polar o bajo la fórmula de Euler18 $u = e^{iΘ}=cosΘ + i·senΘ$, nos aseguramos que $|u|^{2}=cos^{2}Θ + sen^{2}Θ=1$. Es decir, que la suma de los módulos al cuadrado de las amplitudes de probabilidad de todos los estados posibles es igual a 1. De esta forma podemos trabajar los estados de los qubits sobre el círculo unitario, que es de radio 1, centrado en el origen (0, 0) sobre el plano Cartesiano. Este sistema se puede generalizar y extender a tres dimensiones. (Ver Esfera de Bloch y IBM Gates Glossary). La representación esférica de Bloch sólo sirve para describir qubits individuades en un espacio tridimensional, pero no para comprender lo que pasa con múltiples qubits, dado que no puede mostrar entrelazamientos.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ejemplo: Sea A =[0 1] y B= [1 0 0]t, entonces al aplicar la operación matricial de Kroneker, se tiene: 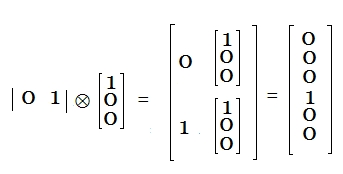 Expresión Matemática de las Relaciones entre los Qubits Un sistema de Estado Básico de n qubits se puede expresar como un producto tensorial de los estados básicos de sus componentes. Es decir, cada uno de los qubits es una componente individual del sistema. En otras palabras, el estado básico del sistema se puede ver como el producto tensorial de los estados básicos de las componentes de un qubit. Ejemplo: $$ \begin{matrix} |00〉 & = & |0〉⊗|0〉 \\ |01〉 & = & |0〉⊗|1〉 \\ |10〉 & = & |1〉⊗|0〉 \\ |11〉 & = & |1〉⊗|1〉 \\ \end{matrix} $$
A continuación se ilustra un ejemplo con los pasos intermedios de cómo opera Kroneker sobre las componentes que un qubit:
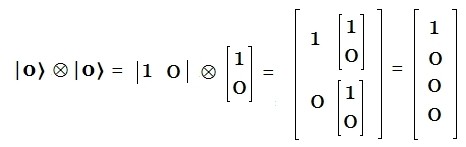 Notación Sintética que Señala la Posición del $1$ Notación para señalar la posición del $1$ en un vector de la base canónica binaria, cuya dimensión es $2{n}$.
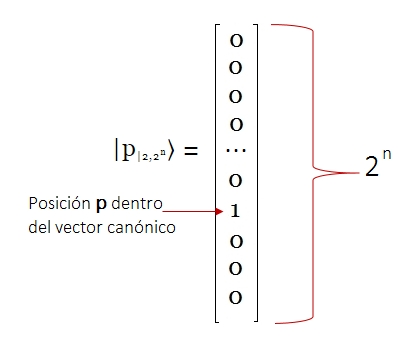 Por tanto, cada estado básico corresponde a un vector de la base $C^{2n}$, dado por la notación $p≤2^{n}〉$ Ejemplo: 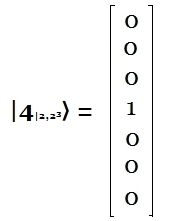 Nótese que en lenguajes de programación (Python o C o Javascript o cuando se utiliza el comando "split" para generar un arreglo, etc..). En ese caso, es necesario hacer una corrección partiendo desde $0$, porque en el presente artículo se usa la convención que empieza a contar desde la posición $0$. Ejemplo: 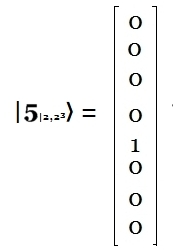 Modo Numérico de Representar los Vectores Unitarios En síntesis se puede utilizar la siguiente notación reducida para representar vectores unitarios con $n$ qubits: Por ejemplo con $n=2$: 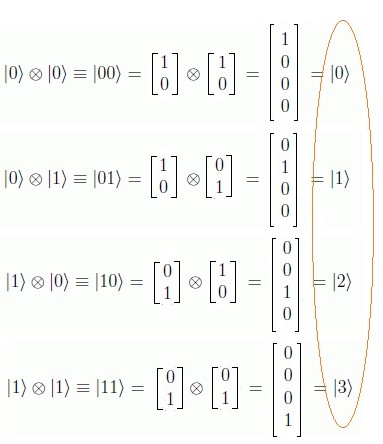 Por ejemplo con $n=3$ qubits: La forma binaria del número $|6〉$ es $|110〉 ↔ 1·2^{2}+1·2^{1}+0·2^{0}$ y la carga de un registro cuántico con este valor se realiza preparando tres qubits en sus estados básicos: 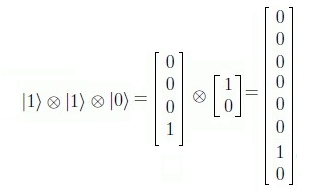 En general, tal con mostró en el párrafo Aplicación Algoritmo Decimal $\longrightarrow$ Binario, la fórmula de un número decimal $x$ se representa en forma binaria como: $$|x〉=\sum_{k=0}^{n-1}x_k·2^{k}$$ Donde $|x〉$ es de la forma $|x_{n-1}\text{ } x_{n-2}\text{ } x_{n-3}\text{ } \ldots\text{ } x_1 \text{ }x_0〉$ y cada $x_i \in \unicode{123}0,1\unicode{125}$. Por ejemplo, el decimal $9$ convertido a binario y representado por la fórmula, se ilustra a continuación: $$|9〉=|1001〉\quad \Rightarrow\quad x_3=1,\text{ }x_2=0,\text{ }x_1=0,\text{ }x_0=1$$ Es decir, $|9〉$ tiene 4 qubits, $|1001〉 ↔ 1·2^{3}+0·2^{2}+0·2^{1}+ 1·2^{0}$ Esta notación $|x〉=|x_{n-1}\text{ } x_{n-2}\text{ } x_{n-3}\text{ } \ldots\text{ } x_1 \text{ }x_0〉$ se utilizará posteriormente al estudiar la Transformada Cuántica de Fourier como paso previo al Algoritmo de Shor.
Estado Producto y Entrelazamiento
Un conjunto de qubits está en Estado Producto si su estado puede expresarse como el producto tensorial de los estados de sus componentes. En caso contrario, se dice que está en Estado de Entrelazamiento. Este fantasmal estado, conocido como entrelazamiento cuántico20, se produce en sistemas de dos o más qubits, cuando algunos qubits podrían formar un único sub-sistema, donde no es posible modificar el estado de un qubit, sin alterar el estado de los otros. Ejemplo Estado Producto: $$ \frac{1}{2}|00〉-\frac{1}{2}|01〉+\frac{1}{2}|10〉-\frac{1}{2}|11〉 =(\frac{1}{\sqrt{2}}|0〉+\frac{1}{\sqrt{2}}|1〉)⊗(\frac{1}{\sqrt{2}}|0〉-\frac{1}{\sqrt{2}}|1〉) \qquad\qquad [3]$$
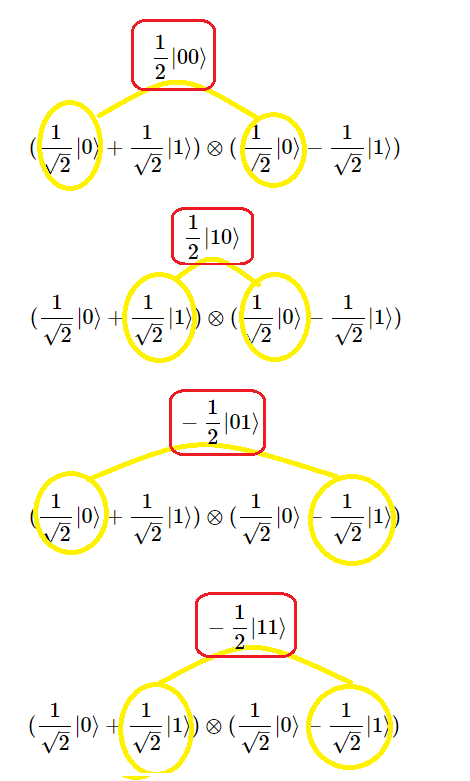 Esta multiplicación tensorial uno a uno de los factores se marcaron en amarillo y sus resultados parciales arriba con rojo. Luego, sumando los términos que se rotularon con el marco rojo se obtiene el primer miembro de la ecuación $[3]$:
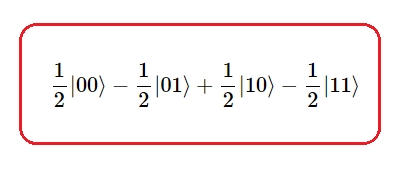 Por tanto es un Estado Producto, dado que la expresión $[3]$, es factorizable, - bajo el producto tensorial- en los estados de sus componentes. Estado Entrelazamiento: Demostrar que la siguiente expresión de qubits representa un Estado Entrelazamiento: $$\frac{1}{\sqrt{2}}(|01〉+ |10〉)\qquad\qquad[4]$$ Demostración: Por demostrar que la expresión no es un Estado Producto. Es decir, que no es posible expresar $[4]$ como el producto tensorial de los estados de sus componentes.
Sean $α_i∈C$ con $i=0,1,2,3$ Entonces: Contradicción, no es factorizable o separable bajo el producto tensorial. Dado que en la expresión $\alpha_0\alpha_2 \neq \alpha_1\alpha_3$, al menos uno de los coeficientes debe ser 0. Por tanto, la expresión $[4]$ representa un Estado Entrelazamiento. Es decir, no existen coeficientes $α_i ∈ C\quad \alpha_i\neq 0$, tales que cumplan o posibiliten la factorización de $[4]$. Esto implica que $[4]$ no puede describirse en función de los estados de los qubits que lo componen.
Los estados cuánticos de esta forma, - que se ilustra en el simulador en el siguiente párrafo -, son especiales y se conocen como Estados Bell. En efecto, cuando se mide cualquiera de los dos qubits, tiene una probabilidad de 50-50 de medir 0 o 1. Pero una vez que se haya realizado su medición en ese qubit, el otro remoto tiene un 100% de probabilidad de ser exactamente lo que midió el primer qubit.
Paralelismo Cuántico
Así mismo, se recomienda consultar la extensión a n-qubit de este algoritmo cuántico, donde el matemático Richard Jozsa en 1992 contribuyó a mejorarlo, tomando el nombre de Algoritmo de Deutsch-Jozsa56. Otro caso importante a consultar y comprender el famoso ejemplo de teletransportación cuántica entre Alice y Bob21.
Esta propiedad de paralelismo admite que una función de múltiples variables f(x1,x3,x3...,xn) que pueden ser operadas en forma simultánea con todas sus variables. Por tanto, supera al clásico sistema computacional basado en bits, dado que es posible tener un número exponencial de estados en un espacio reducido y el sistema cuántico realiza de una sola vez todas las computaciones posibles.
A continuación, se esquematiza un simulador de donde se sacan 5 cartas aleatorias de un Naipe Inglés de 52 unidades.
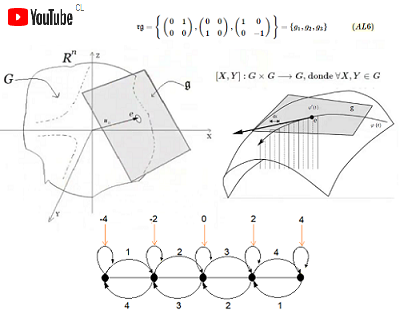
La forma más directa y sencilla de ilustrar esta propiedad con dos entradas, es con una variante de la transformación unitaria CNOT, que desarrolló David Deutsch del Instituto Matemático de la Universidad de Oxford y que actualmente es uno de los algoritmos pilares de la computación cuántica. (Ver Desarrollo Algoritmo de Deutsch más adelante) Estados Cuánticos Frecuentes Importantes Estados equiprobables de un qubit. Paradoja de Bell, donde {$|+〉 , |-〉$} es también una notación utilizada frecuente de la Base de Hadamard. $$|+〉=\frac {1}{\sqrt{2}}(|0〉+ |1〉$$ $$|-〉=\frac {1}{\sqrt{2}}(|0〉- |1〉$$ Estado de Bell o Paradoja EPR (Einstein-Podolsky-Rosen: "A. Einstein, B. Podolsky and N. Rosen, Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?, Physical Review 47 (1935) 777-780). $$\frac {1}{\sqrt{2}}(|00〉- |10〉)\quad\leftarrow \mathbf {Estado\quad de\quad Etrelazamiento\quad Estándard}$$ El experimento planteado por EPR consiste en dos partículas que interactuaron en el pasado y que quedan en un estado entrelazado. La paradoja EPR está en contradicción con la Teoría de la Relatividad22, ya que aparentemente se transmite información de forma instantánea entre las dos partículas. Estos tres grandes científicos denominaron el fenómeno como "spooky action", i.e como una acción escalofriante. (Ver a continuación Simulador de Entrelazamiento Cuántico).
Las partículas representadas por los dados en el simulador23, corresponden a un, -vector de más de un qubit-, Estado No Producto o Estado de Entrelazamiento. Es decir, es un estado que no es posible factorizar o separar su formulación matemática. Por tanto, los eventos no son independientes y la probabilidad de la medida, - probada experimentalmente-, es exactamente igual (o contraria) entre los qubits a raíz del cambio. Puertas Lógicas Clásicas
Para manejar la información almacenada en un conjunto de bits, utilizamos las llamadas Puertas Lógicas, que se basan el Algebra de Bool o Lógica Proposicional con tres conectivas básicas y sus variantes: ~p, p ∨ q, p ∧ q, p ⇒ q, p ⇔ q, (p ⇒ q) ⇔ (~p ∨ q), etc.. Junto a las Leyes de Morgan.
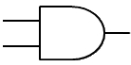
Puerta AND
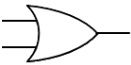
Puerta OR
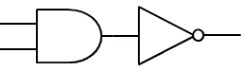
Puerta NAND Existe una puerta lógica NAND, que es particularmente importante en computación, la cual es una composición de AND con NOT. Esta conectiva tiene una propiedad de universalidad24 y es muy utilizada en la programación. En efecto, cualquier circuito lógico clásico se puede hacer con una concatenación de puertas NAND.
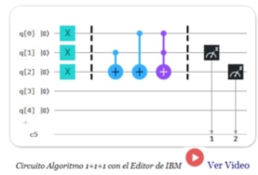
Ejemplo de Suma de $1+1+1$ con Computación Clásica con Bits   Circuito Cuántico 1+1+1 con Composer Quantum IBM Circuito Cuántico 1+1+1 con Composer Quantum IBM
La idea del ejemplo es explicar lo más detalladamente posible el desarrollo de esta suma con computación clásica, con el objeto de ir preparando en forma preliminar el algoritmo 1+1+1 con qubits, que ilustraremos más adelante con el Composer Cuántico de IBM. En este ejercicio de computación clásica se utiliza un operador de Thomas Toffoli, que en los años 80 junto a Edward Fredkin descubrieron que se requería un mínimo de tres qubits, - para cualquier computación clásica-, a fin conservar la Reversibilidad.

Tabla Suma 1+1+1 con con Bits Explicación de Suma de $1+1+1$ con Bits
Algoritmo-Interfaz Suma Números Binarios
Sumar números binarios es semejante a la operación simple que se aprendió en la escuela con números decimales, pero la Suma es Modulo $2$.
Nótese que $1⊕1=0$ y se reserva $1$, el cual se adiciona a la siguiente posición. En caso de que quede en una posicion o columna la suma de 3 unos ($1 ⊕1 ⊕1=1$), entonces se reserva $1$ para la siguiente posición, y así sucesivamente.
Esta operación clásica que se aplica en cuántica (Ver más adelante Circuito Suma Toffoli-CNOT), donde se muestran las pautas para sumar simultáneamente con una única unidad de control.
El camino hacia la construcción consolidada de una computadora u ordenador cuántico proviene del hecho de que algunos algoritmos funcionan significativamente y más eficazmente en una computadora cuántica
que en una computadora clásica.26
 Estados Básicos y Estado en Superposición. Ambos son Estados Únicos.
A fin manejar la información almacenada en un conjunto de qubits y extraer información útil utilizando la interferencia cuántica, utilizamos Puertas Cuánticas. La definición de una puerta cuántica requiere conocer su efecto sobre los estados básicos y se necesita saber también cómo se comporta con una combinación lineal. Las leyes de la mecánica cuántica nos dicen que la evolución de un sistema responde a la Ecuación de Schrödinger29 (si no se realiza una medida). Se reitera que en el presente artículo sólo está enfocado en la matemática computacional y no en la física cuántica que es la fuente experimental de donde derivan la mayoría de los postulados que iremos mostrando a los largo de los capítulos y versiones del documento. En síntesis para definir una Puerta Cuántica y es necesario que una matriz para:
Ejemplo de Matriz Unitaria Demostrar que la matriz $A$ es Unitaria.
$∴\quad A$ es una matriz Unitaria, dado que $A^{t}=A^{*}$, donde $AA^{*} = A^{*}A = I$. Es decir, la matriz conjugada es la inversa, $A^{*} = A^{-1}$. Por demostrar que $A^{*}=A^{-1}$
QED. Puertas Lógicas Cuánticas
Una Puerta Lógica Cuántica es un circuito cuántico básico que opera sobre un pequeño número de qubits.
El concepto y construcción de puertas cuánticas es innumerable, dado que pueden ser composiciones que se configuran con operaciones simples. Estas puertas se representan con matrices unitarias que actúan sobre las amplitudes de probabilidad de los qubits. Pero las puertas primitivas o que se denominan universales, - ver IBM Experiencia Cuántica Editor de IBM QX -, son matrices 2×2 que cumplen con todas las condiciones antes especificadas previamente.
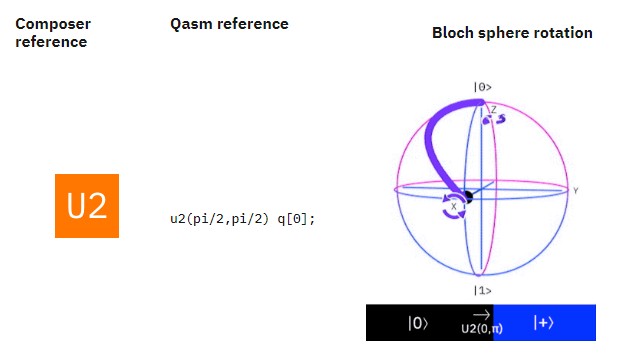
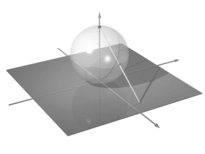
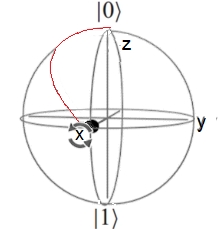
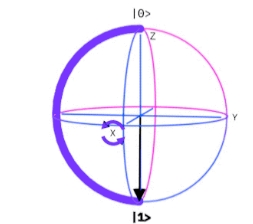
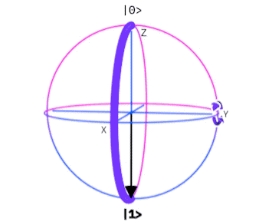
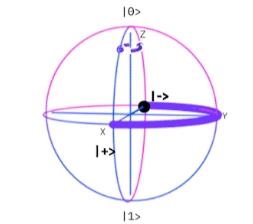
En la Ayuda en línea del Composer de IBM, se describen gráficamente las puertas lógicas cuánticas simples (Por ejemplo las de Pauli y los operadores matriciales $U_n$ y otros), utilizando la Esfera de Bloch. Esta representación es un herramienta de visualización importante para comprender lo que sucede con un circuito cuántico.
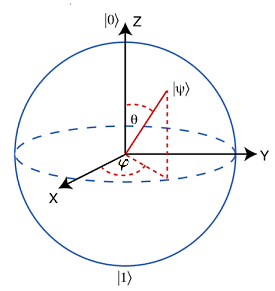 Esfera de Bloch. Fuente: IBM Quantum Experience
La Esfera de Bloch, se utiliza con el fin didáctico para comprender la variación del qubit, - restringido sólo como objeto tridimensional-, bajo la aplicación de los operadores.
$$|\psi〉=cos(\frac {\theta}{2})|0〉+(\cos\theta+ i\ \sin \ φ)\sin(\frac {\theta}{2})|1〉$$
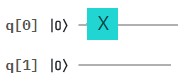
A continuación las tres matrices de Pauli31, X, Y, Z que tienen gran utilidad en la computación cuántica, son prácticamente imprescindibles en la programación de circuitos cuánticos.
Debemos buscar un operador $X$, tal que: i) $|0〉 → |1〉$ y $|1〉 → |0〉$ Es decir, esta puerta Pauli $X$ , opera como una puerta $NOT$, cambia de un estado básico a otro (viceversa). La puerta $NOT$ es equivalente a la puerta $RX$ (del IBM Quantum Composer), para el ángulo $\pi$ radianes de rotación en torno al eje de las $x$.
La puerta de Hadamard es muy importante y consecuentemente utilizada en los algoritmos de la computación cuántica, porque se presta para ir aprovechando las ventajas de manejo de la evolución de los estados en superposición, hasta llegar a un lugar que medir esa superposición sea útil para contribuir a solucionar el problema con el algoritmo en cuestión.

 Ver Video Montecarlo-Hadamard Ver Video Montecarlo-Hadamard
Es decir, Hadamard es una puerta de un qubit muy apropiada para generar superposición equiprobable, donde no se favorece ninguno de los estados básicos. 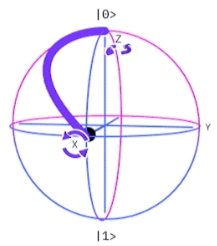 $H$ ibm quantum experience-fuente gates glossary En general, cuando se comienza a construir un algoritmo cuántico, se establece un conjunto de qubits de inicialización en estado cero, pero se prepara el circuito para introducir los estados en superposición equiprobables con Hadamard. Nótese que la puerta lógica cuántica de Hadamard $H$, se puede expresar como una combinación de las puertas universales de Pauli, $X$ y $Z$ 84. En efecto, $H=\frac{1}{2}(X + Z)$, lo que es fácilmente comprobable: $ \large{\frac {1}{\sqrt{2}}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \\ \end{pmatrix} $ = $\large{\frac {1}{\sqrt{2}}}$ $ \Biggl( \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix} $ + $\begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix} \Biggr)$ Ahora, si se aplica el producto tensorial $⊗$ con $H$ sobre vectores de varios qubits (operador de Walsh-Hadamard), utilizando la notación en $n$, descrita previamente en Modo Numérico de Representar los Vectores Unitarios. Este producto tensorial con Hamadard, se describe mediante la siguiente expresión: $$H ⊗ H ⊗ H ⊗\cdots H |\underbrace{0 0 0\cdots 0}_{n\text{ veces}}〉=\frac {1}{\sqrt{2^{n}}}\sum_{x=0}^{2n-1} |x〉$$ Por ejemplo, con $n=2$: $$H ⊗ H |00〉=\frac {1}{\sqrt{2}}(|0〉+|1〉) ⊗ \frac {1}{\sqrt{2}}(|0〉+|1〉)=$$ $$\frac{1}{2}(|00〉+|01〉+|10〉+|11〉=$$
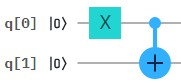
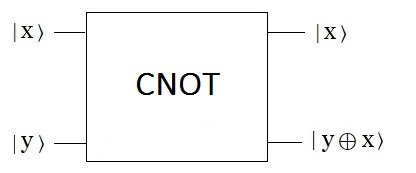
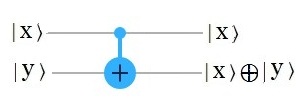
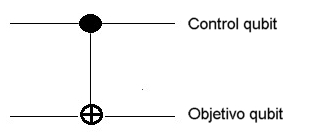
La Puerta cuántica $CNOT$ es una puerta no controlada. Las puertas controladas operan sobre 2 qúbits o más. En este caso su efecto es: Para el Algoritmo de Deutsch, es clave comprender la importancia del operador controlado $CNOT$ (denotado como $CX$ en el Composer Quantum de IBM), que se aplica con al menos $2$ qubits. 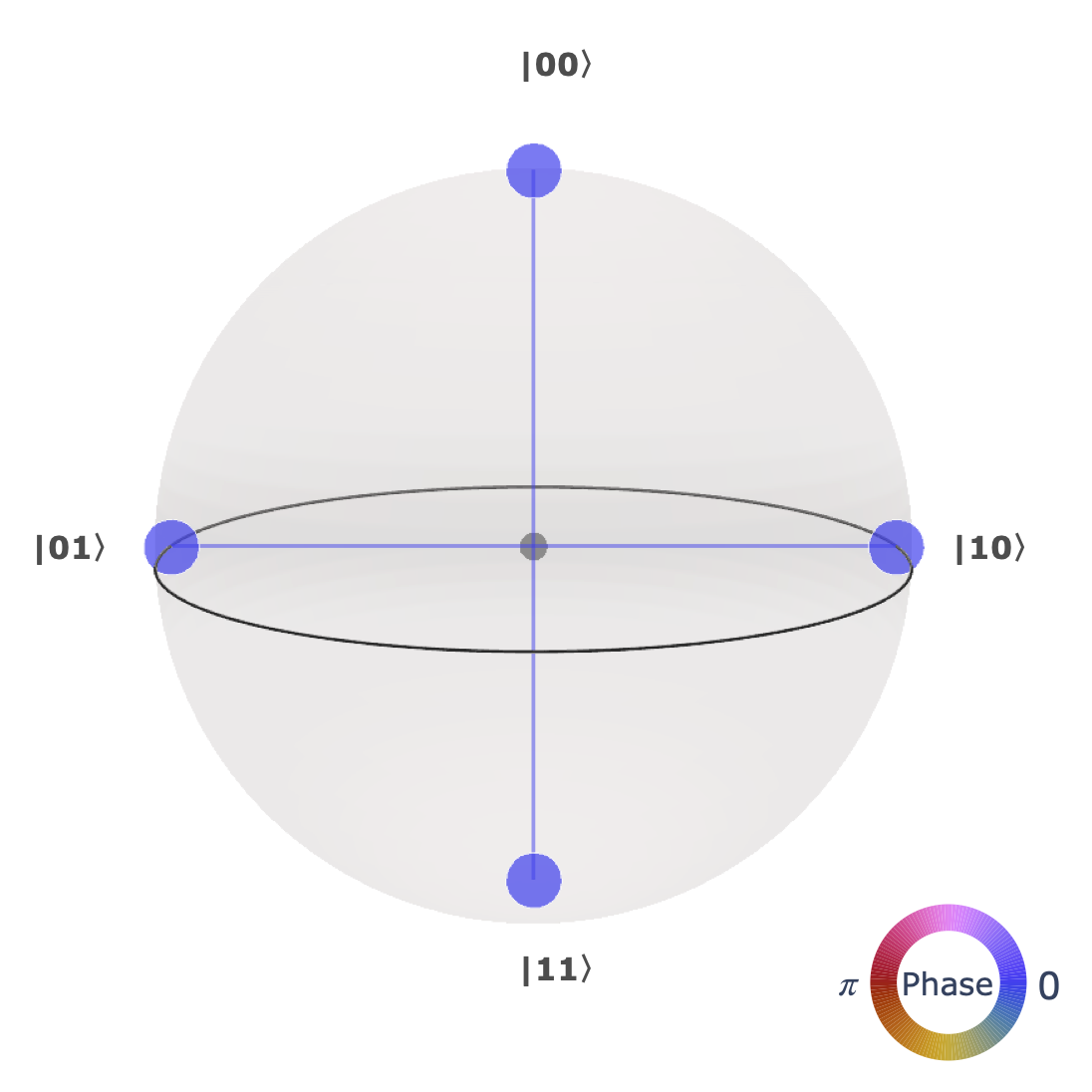 $CNOT$ ibm quantum experience-fuente gates glossary A diferencia de las Puertas de Pauli, - descritas previamente -, las cuales son transformaciones unitarias, i.e. de un qubit y pueden ser representadas en sus dos estados por su rotación en los ejes de la Esfera de Bloch. Así mismo, la puerta de Hadamard, - que rota sobre el eje de las ordenadas $Y$ -, juega un rol preponderante de superposición en el Algoritmo de Deutsch. Nótese que si el qubit de control del operador $CNOT$ está en un estado de superposición, se crearán entrelazamientos (Ver Estado de Bell). En efecto, la transformación $CNOT$ es una puerta de $2$ qubits de entrada. Se ilustra a continuación:
El primer qubit $x$ se llama control. El control es invariante en la transformación. El segundo qubit $y$ se llama objetivo. El objetivo se niega cuando $x$ = $1$. Es decir, $y$ no cambia si $x$ = $0$. La operación $⊕$ es la conectiva ∨ (XOR) que corresponde al OR excluyente en el Algebra de Boole. La operación $⊕$ se utiliza como la llamada suma módulo $2$. Es decir, el primer bit de entrada $x$ siempre se pasa directamente; el segundo bit se aplica sí y solo sí el bit de "control" $x$ es $|1〉$, i.e. aplica un Pauli $X$ en el objetivo. Para ser aún más explícito, $CNOT$ tiene la siguiente tabla de verdad:
Para explicar paso a paso la Matriz $CNOT$, Consideremos los vectores de base $|0〉$ y $|1〉$. Apliquemos a cada columna la operación $CNOT$ antes definida y veremos que las dos primeras columnas permanecen invariantes por que el qubit de control es $0$, y las dos últimas columnas cambian porque el qubits de control es $1$, obteniendo la siguiente matriz: $$ CNOT= \begin{pmatrix} 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ \end{pmatrix} $$
Puerta de Toffoli
La puerta de Toffoli cubre la necesidad de tener un mínimo de tres qubits para cualquier computación clásica. La extensión a tres qubits de la puerta CNOT se denota como CCNOT o también Puerta de Toffoli (En el "Composer de IBM", el objeto se denomina CX). Para eso, se definen dos bits de control que sólo actúan si están a $1$.
Al aplicarla dos veces resulta la identidad. Por tanto, es una puerta reversible (su inversa es ella misma). La expresión matricial es:
La puerta clásica de Toffoli es una transformación de 3-qubits que cambia el tercer qubit, cuando los dos primeros son $1$. Evidentemente es una transformación unitaria. La puerta de Toffoli, es de gran utilidad en el diseño de algoritmos cuánticos, permite equipararlos con algoritmos de computación clásica, ya que es universal para la computación booleana. Más adelante se utilizará en los ejemplos con el Editor Composer de IBM, también en forma extendida atravesando más cables (o qubits) y con puertas equivalentes como $U_3$32. Su representación es el siguiente diagrama: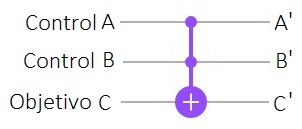 Diagrama Puerta Toffoli o CCNOT  Tabla Síntesis con Entradas y Salidas Toffoli
A fin de manipular recursos "algebraicos" en la construcción de algunos circuitos cuánticos es necesario introducir puertas lógicas cuánticas ternarias. Toffoli es una de ellas, dado que es una puerta NOT con dos controles previos al objetivo.
Si se observa, tanto la representación matricial como la Tabla de Entradas y Salidas de la Puerta de Toffoli, se determinará que la resultante $C^{'}$, obtenida mediante operaciones booleanas, se expresará con la siguiente proposición lógica:
Ahora, que ya se describieron las puertas cuánticas elementales, se complementa lo tratado en previamente en Algoritmo - Interfaz Suma Números Binarios, a fin de ir introduciendo un simple circuito cuántico para las sumas de dos bits. Utilizando las Puerta de Toffoli y CNOT, - donde las entradas $x, y \in${$0,1$} -, con el tercer qubit en cero. Se ilustra el siguiente diagrama: 
Circuito Cuántico ~ Suma Toffoli y CNOT
Son concatenaciones de puertas cuánticas o una sucesión de modificaciones de un conjunto de qubits, que producen consecutivos cambios de estado en un ordenador. Esta notación gráfica de diagramas, se expresa mediante cables horizontales (uno por qubits) sobre los cuales se localizan las puertas cuánticas. Se leen de izquierda a derecha. A continuación una imagen animada de ejemplo extraído de "IBM Q, Introduction to Quantum Circuits, Getting started with quantum circuits URL: https://quantum-computing.ibm.com/".
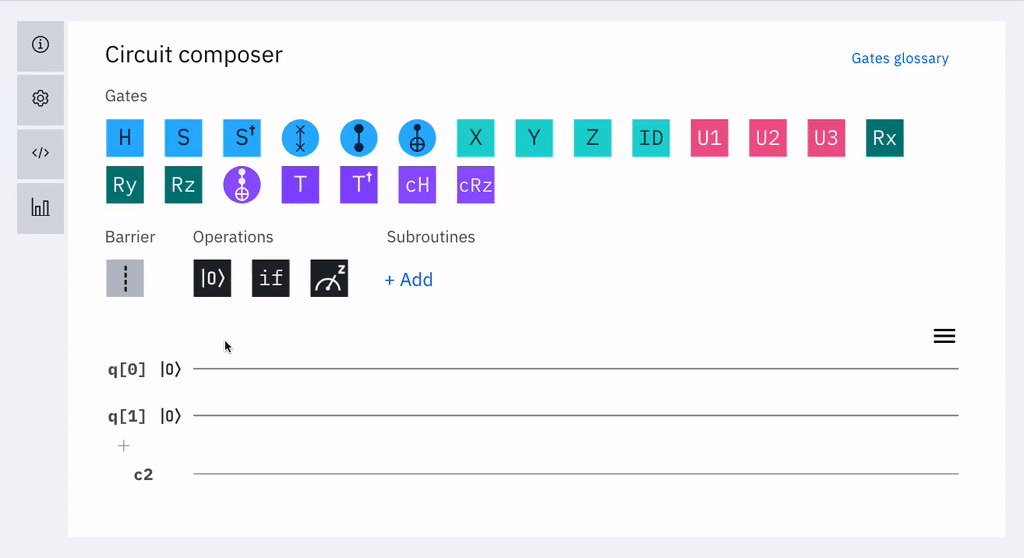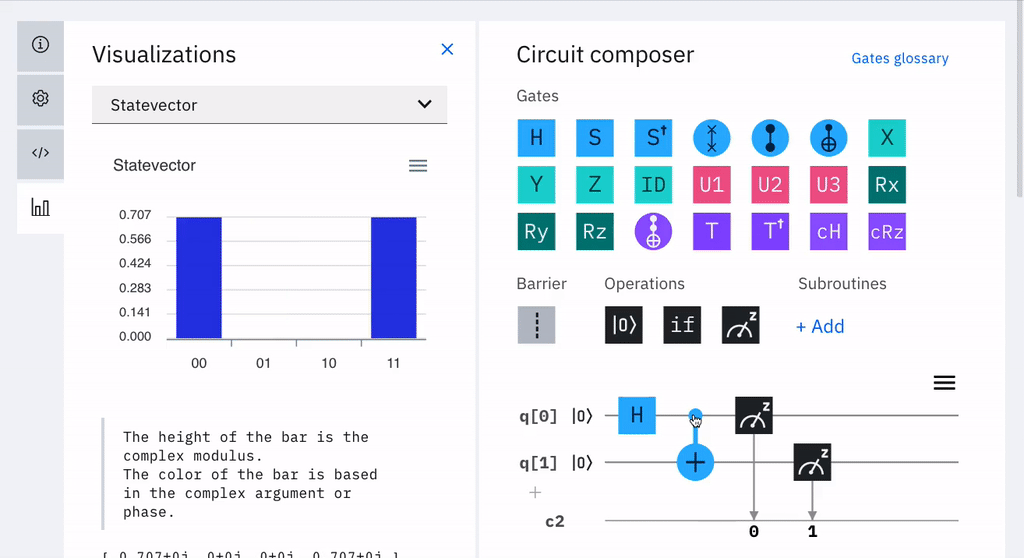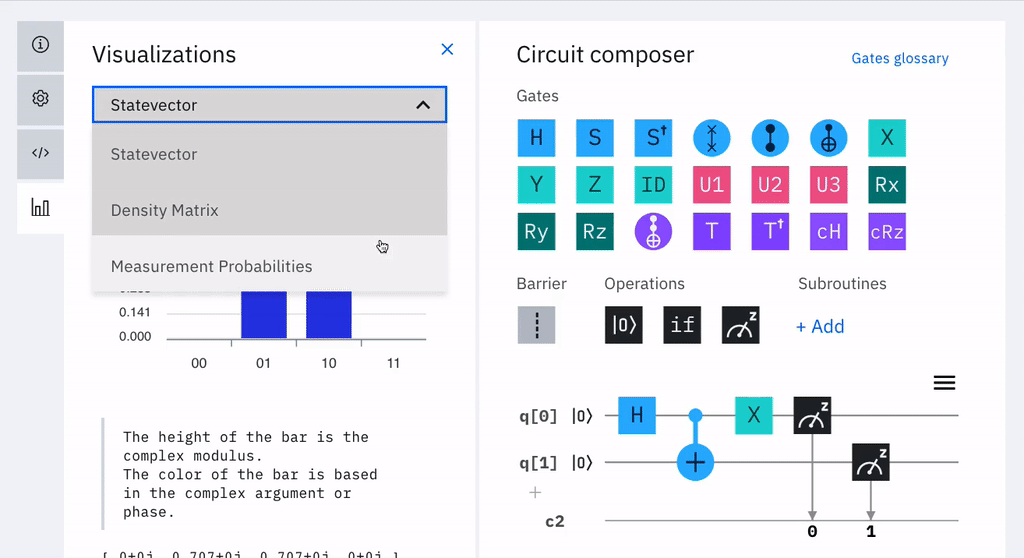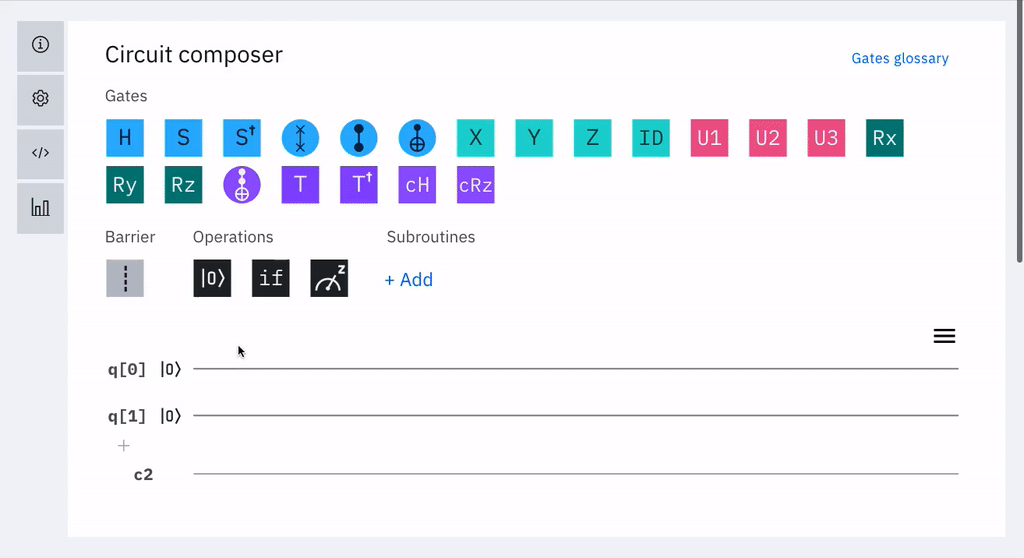
Vista Principal del Editor Circuit Composer de IBM En un siguiente ejercicio se construirá el algoritmo que calcula 1+1+1, describiremos detalladamente paso a paso el cicuito cuántico utilizando el Composer de IBM. Nótese que generalmente los qubits de los algoritmos se inicializan en cero. La notación q[0],q[1],..q[n] para descomponer los qubits. Por ejemplo: |001〉 se presenta como q[0]=0, q[1]=0 y q[2]=1.(Revisar operador Barrier33)  Circuito Algoritmo 1+1+1 con el Editor de IBM  Ver Video Ver Video
Los Estados de Bell son cuatro específicos estados cuánticos máximamente entrelazados de dos qubits. Están en una superposición de $|0〉$ y $|1〉$ , i.e. en una combinación lineal de estos dos estados.
 Descripción de los Pasos del Circuito Los pasos aplicados en este circuito cuántico para crear un estado de Bell son los siguientes: 1.- La puerta de Hadamard transforma el primer qubit q[0] a un estado de dos qubits: $${(|0〉+|1〉)|0〉\over \sqrt{2}}{={(|00〉+|10〉)\over \sqrt{2}}}$$ 2.- A continuación, a ese resultado se le aplica el CNOT: $${(|0\ \ 0⊕0〉 + |1 \ \ 0⊕1〉)\over\sqrt{2} }$$ 3.- Por lo tanto se obtiene: $${(|00〉+|11〉)\over\sqrt{2} }$$  Circuito con el Editor de IBM  $$|00〉\rightarrow \frac {1}{\sqrt{2}}(|00〉+|11〉)\rightarrow \frac {1}{\sqrt{2}}(|00〉+|11〉) \rightarrow \frac {1}{\sqrt{2}}(|00〉-|11〉)$$ El mismo circuito con el Editor de IBM se obtiene el siguiente resultado: 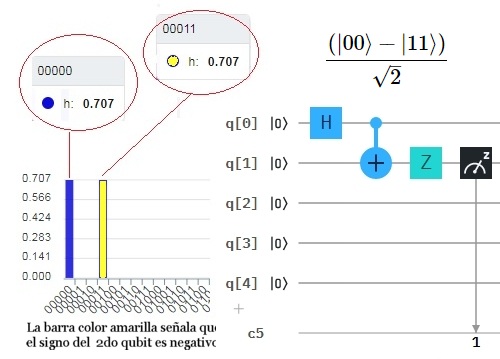 Circuito con el Editor de IBM Ejemplo de Indempotencia34 con CNOT Dado el siguiente diagrama de Puertas Cuánticas. ¿Cuál es el resultado? Resultado:  Dos puertas Hadamard en serie resultan en un qubit con el estado original.  H H H H |ψ〉 |ψ〉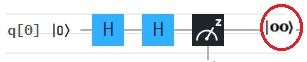 Se puede ver claramente que este mapeo es una biyección 35, lo que confirma que CNOT es una puerta reversible. (Ver una generalización pequeña pero importante, llamada CCNOT (control controlado-NO) o Puerta Toffoli.) Ejemplo de Algoritmo con Puertas de Pauli
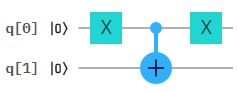
Construir un algoritmo que transforme un qubit en estado |0〉 a un estado -|0〉   Circuito con el Editor de IBM |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Preparando el Camino para Comprender el Algoritmo de Deutsch57
El objetivo principal es culminar este capítulo Algoritmo de Deutsch, - que constituye el núcleo del presente trabajo-, exponiendo y explicando el desarrollo paso a paso de la fórmula simplificada del estado cuántico resultante $\color{black}{\mathbf{|ψ_3〉}}$ del circuito del Algoritmo de Deutsch. Al finalizar su deducción en la próxima sección, la fórmula será rotulada como $[6]$.
Mediante esta formulación compacta mostraremos ulteriormente, - después de la descripción de una serie de detalles-, que con sólo evaluar $f(0)$ se podrá saber si la función es constante o balanceada. Ciertamente, al pasar por la caja negra u oráculo de Deutsch, se medirá el primer qubit del estado de salida sobre un vector de la Base de Hadamard103$\unicode{123} |+〉, |-〉\unicode{125}$. Si después de medir obtenemos dentro de la resultante la expresión $\frac {1}{\sqrt{2}}(|0〉+|1〉)$ entonces la función es constante, y si obtenemos $\frac {1}{\sqrt{2}}(|0〉-|1〉)$ la función es balanceada.
Más adelante, se mostrará con más detalles mediante el diagrama de árbol que se ilustra a continuación, cómo se ejecuta "de una" el algoritmo.
Es decir, todas las combinaciones simultáneamente, utilizando la propiedad del parelismo cuántico.
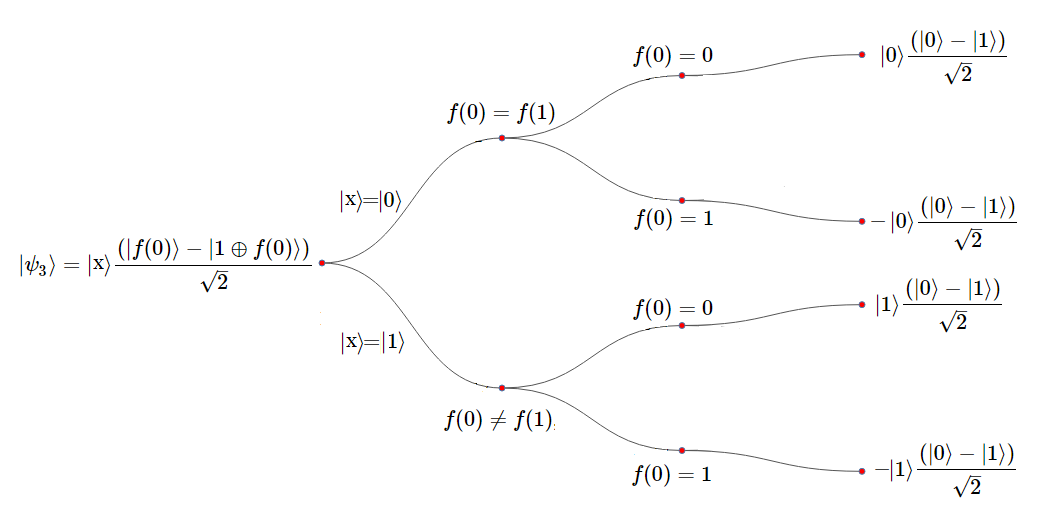 Diagrama de Árbol $U_f$: Casos y Alternativas de $|\psi_3〉$ La metodología esencial se basa en desagregar todas las evaluaciones posibles, aplicar algunos recursos algebráicos y finalmente expresar la fórmula en función de $x$ y $f(x)$, ambas definidas sobre $\unicode{123} 0,1 \unicode{125}$ respectivamente. Teniendo presente que la aplicación de este proceso se ejecuta en tiempo cero, sobre un computador cuántico que aprovecha el paralelismo inherente de los estados en superposición.
Los circuitos que se derivan del Algoritmo de Deutsch tienen la capacidad de evaluar el resultado de todas las posibles combinaciones de los estados cuánticos en un breve número de ciclos de ejecución.
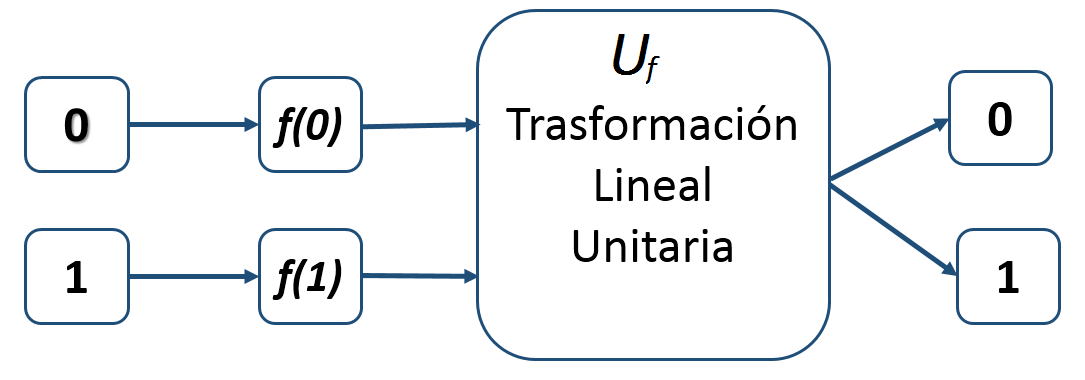
Modelo ~ Problema de Deutsch Si bosquejaramos una rutina con programación clásica y lineal, la idea central del operador lógico del Algoritmo de Deutsch sobre una función $f(x)$, se vería como el Javascript que se ilustra a continuación:
Es decir, se requieren al menos 2 chequeos en el algoritmo de un sistema de computación clásica con un bit para determinar si una función $f(x)$ es constante o balanceada.
Formalizando, sea $f${$0,1$}$^{n}\longrightarrow$ {$0, 1$} una función booleana ($f \unicode{123} 0,1 \unicode{125}^{n}=f\unicode{123}x_1,x_2,x_3,\dots,x_n\unicode{125}$). Entonces $f(x)$ se dice ser Constante si $f(x)$ no cambia para cualquier posible valor de entrada, i.e. $f(x)$ invariante $∀x ∈${$0,1$}$^n$.
Ejemplo: Todo número que ingresa se transforma en $0$ Por otro lado, $f(x)$ se dice Balanceada si $f(x)=0$ para la mitad de las opciones de entrada y $f(x)=1$ para la otra mitad. El procedimiento cuántico para funciones $f${$0,1$}$^{n}$ de $n \geq 1$ entradas, que incorporó el matemático Richard Jozsa en 1992 al Algoritmo de Deutsch56 es una extensión en $n$ y resuelve más rápido la determinación si la función $f(x)$ es Balanceada. Es decir, toma $n$ bits de entrada {$x_1, x_2,..., x_n$} y devuelve un valor binario $f(x_1, x_2,..., x_n$), sea $0$ o $1$.
Ejemplo: Entradas $1,2,..10$ y Salidas {$0,1$}
La optimización del resultado dice relación con el tiempo de ejecución en función del tamaño de la entrada. Para establecer este hecho, ilustremos la solución convencional (Ver Lunch & Learn: Quantum Computing). Hagamos entonces un conteo que muestre que el número de veces del valor $0$, el cual debe ser el mismo número de veces que asume el valor $1$. Es decir, sea $A_0$ el conjunto de funciones en cero y $A_1$ el conjunto de funciones en uno. Entonces:
$A_0 ={\unicode{123}x\in f{\unicode{123}0,1\unicode{125}}^{n} / f(x)=0\unicode{125}}\quad\Rightarrow \quad \unicode{35} A_0 = 2^{n-1}$
Donde el símbolo $\unicode{35}$ denota la cardinalidad del conjunto y se requiere determinar el máximo de pasos para decidir si $f(x)$ pertenece a $A_0$ o no. Sea $F_n$ el conjunto de todas las $n$ funciones booleanas constantes o balanceadas, i.e. $F_n=A_0 \cup A_1\quad$ ($A_0 \cap A_1=\emptyset $, dado que es una partición).
Obviamente la suma de ambas cardinalidades, #$(A_0 \cup A_1)$ dan exactamente la cardinalidad de $\unicode{35}F_n=2^{n-1} + 2^{n-1} = 2^{n}$
Por ejemplo, consideremos el número de funciones booleanas balanceadas sometidas a dos entradas.
Donde la tabla de cardinalidad, #$F_2=8$, consta de $6$ funciones baleanceadas que se muestran con fondo amarillo ($f_1,f_2,\dots ,f_6$) y $2$ funciones constantes ($f_0, f_7$) que se muestran con fondo blanco.
$F_3$: 70 Combinaciones Balanceadas ¿Por qué y cómo se aborda cuándo $f${$0,1$}$^{n}$ es balanceada en cuántica?
Nótese que justamente el Algoritmo de Deutsch-Jozsa resolvió ¡de una! este problema, utilizando qubits y la propiedad del parelismo cuántico, logrando una solución de complejidad computacional.
$$f(0,0,0,\dots ,0)\longrightarrow 0 \quad y \quad f(0,1,0,\dots ,0)\longrightarrow 1$$
Por otro lado, si se va iterando el sistema e ingresando cadenas de $n$ bits en el algoritmo y la función va arrojando la misma salida, entonces habría que continuar verificando hasta más de la mitad de los ingresos, a fin de evidenciar este resultado y constatar que la función $f(x)$ es constante.
Ahora ilustremos algunos ejemplos: i) Si $f(x)$ es Constante entonces:
A continuación la tabla con los 4 posibles resultados de la función binaria $f$. Función $f$ que se describe como constante cuando ambos resultados son el mismo, o balanceada si el resultado de $0$ y $1$ ocurre con la misma frecuencia.
La solución Cuántica: Operador Unitario $U_f$ En esta sección se continúa preparando la comprensión del Algoritmo de Deutsch y sus proyecciones, intenta alumbrar la importancia del operador unitario $U_f$ ,- que detallaremos en la solución cuántica-. Es decir, se abrirá la "caja negra" u oráculo que realiza esta transformación, la cual se aplica en una sola evaluación de $f(x)$, para determinar si es constante o balanceada. La pregunta que responde David Deutsch es muy simple:
Efectivamente la pregunta es simple. Sin embargo formularla en el ámbito cuántico requiere un complejo e inteligente algoritmo que resolvió brillantemente el físico-matemático Davis Deutsch, dando un paso muy importante en el desarrollo de computación cuántica.36
$U_f$ es también llamada por muchos autores como "Función Oracle" u "Oráculo Cuántico (porque es una puerta a la que se le formula una pregunta)" o "Caja Negra" . Incluido el propio David Deutsch que lo utiliza, - con su correcto significado en Inglés-, en sus publicaciones y vídeos. En el caso del presente artículo, en general se ha evitado referirse con el término Oracle a esta matriz unitaria, a fin de no confundir a los equipos de desarrollo informático, quienes están más acostumbrado de llamar así a la marca de un motor de bases de datos que utilizó ese nombre.
$U_f$ se construye a partir de las Puertas Lógicas Hadamard y CNOT que se trataron en el párrafo Computación Cuántica y Puertas del documento central.
Es necesario recordar que, la puerta lógica de Hadamard $H$ es reversible. En efecto, la aplicación en serie del operador $H$ sobre un estado cuántico
cualquiera, devuelve el estado inicial $H^{n} = I$, i.e. $H$ es idempotente en serie. No obstante, su aplicación en
paralelo en un circuito cuántico, genera el producto tensorial de los estados superpuestos.
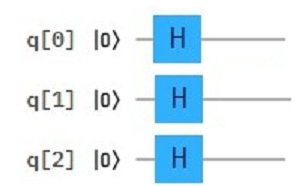 $$H ⊗ H ⊗ H |000〉=\frac {1}{\sqrt{2}}(|0〉+|1〉) ⊗ \frac {1}{\sqrt{2}}(|0〉+|1〉) ⊗ \frac {1}{\sqrt{2}}(|0〉+|1〉)$$
Así mismo, repasemos también la operación de la puerta cuántica $CNOT$, la cual es una puerta no controlada, que opera sobre 2 qúbits o más:
A continuación se ilustrará en una Tabla $U_f$ 2-qubit, con cada uno de los 4 vectores que se obtienen al aplicar el Oráculo Cuántico sobre 2 qubits. Atención, porque los valores obtenidos de esta transformación unitaria será útil tenerlos presente. Dado que en el desarrollo algebraico de la demostración del Algoritmo de Deutsch, se realizarán ciertas sustituciones con los qubits registrados en esa tabla. ($|xy〉→|x\quad y⊕f(x)〉$). Entonces, aplicando el operador $U_f$ a cada uno de los vectores de $2$ qubits, se tiene lo siguiente: 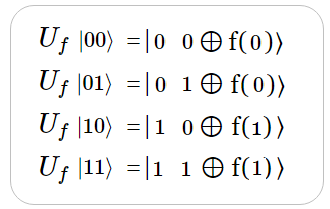 Tabla $U_f$ 2-qubit Ahora, para ilustrar cómo opera $U_f$, tomemos un estado normalizado de $2$ qubits. Sea
La matriz $U_f$ actúa sobre todos los elementos que constituyen el ket $ψ$ en forma simultánea. A diferencia de lo que sucede con la puertas lógicas de la Computación Clásica, donde un bit puede asumir solamente un valor cero ó uno.
$$U_f|\psi〉 = \frac {1}{2}U_f(|00〉 + |01〉 + |10〉 + |11〉)$$ $\Rightarrow$$$U_f|\psi〉 = \frac {1}{2}(U_f|00〉 + U_f|01〉 + U_f|10〉 + U_f|11〉)$$
Téngase presente, - para más adelante-, que cuando se aplica
Algoritmo de Deutsch
La importancia del Algoritmo de Deutsch es que inició y entregó la pauta para solucionar problemas de complejidad exponencial en forma conjunta. Hecho que en computación clásica se debe realizar linealmente en serie. Esto, gracias a que el número de qubits (2n) se ingresan paralelamente. El algoritmo aprovecha el uso de la puerta de Hadamard para preparar una superposición que represente todas las combinaciones posibles.
Tradicionalmente se requieren sólo dos medidas para calcular el resultado, dado que desde ahí es posible deducir la formulación general de su aplicación. Aquí en el presente enfoque, desarrollamos los dos casos y sus $4$ variantes, a fin de explicar este ingenioso pero complejo algoritmo de David Deutsch. Para explicar el desarrollo algebraico paso a paso del algoritmo y llegar a una solución compacta (Ver más adelante $[6]$), aparecen los vectores en estado de superposición de la Base de Hadamard, como primera intervención, después de la iniciación de los qubits $q[0]$ y $q[1]$ . Comenzamos con el estado: 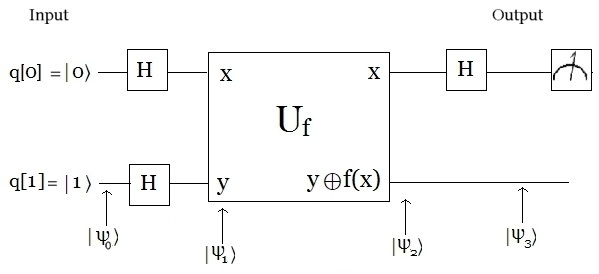 Arquitectura del Circuito Cuántico de Deutsch
La figura muestra un esquema con las transformaciones cuánticas $|\psi_1〉$, $|\psi_2〉$ y $|\psi_3〉$ que se aplican sobre el estado inicial $|\psi_0〉=|01〉$ para resolver el problema de Deutsch. De hecho, son estas tres transformaciones son las que constituyen el Algoritmo de Deutsch.
El operador unitario $U_f$ está definido de tal manera que no afecta el qubit $x$, pero si actúa realizando la operación $y⊕f(x)$ sobre el qubit $y$. Donde reiteramos la operación $⊕$ es la suma módulo $2$. De modo que este operador unitario puede ser implementado por una combinación de estados cuánticos de una puerta de uno o dos qubits.
$U_f|01〉=$ $U_f|0〉|1〉=|0〉|1⊕f(0)〉$ $U_f|10〉=$ $U_f|1〉|0〉=|1〉|0⊕f(1)〉=|1〉|f(1)〉$ $U_f|11〉=$ $U_f|1〉|1〉=|1〉|1⊕f(1)〉$ $\therefore$
En resumen, la función $f(x)$, definida en el dominio binario {${0, 1}$}, con un rango o imagen sobre {${0, 1}$}. Es decir, $f$:{$0, 1$} $\longrightarrow${${0, 1}$}, implica que se configuran cuatro alternativas, clasificadas en dos casos posibles, que se analizarán a continuación: Caso $1$:
$\Rightarrow$ $${|ψ_2〉 ={(|0〉 + |1〉)(|f(0)〉 - |1⊕f(0)〉)\over 2} }$$
Al aplicar la operación Hadamard, H|ψ2〉=|ψ3〉, se obtiene: $${|ψ_3〉 =|0〉 {(|f(0)〉 - |1⊕f(0)〉)\over \sqrt{2} } }$$ Veamos uno a uno las opciones de este resultado del Caso $1$, cuando $f(0)=f(1)$. Es claro que en caso de igualdad $f(0)⊕f(1)=0$ 41
Caso $2$: $${|ψ_2〉 ={(|0\ f(0)〉 - |0\ \ 1⊕f(0)〉 + |1\ f(1)〉-|1\ \ 1⊕f(1)〉)\over 2}}$$ $\Rightarrow$
Al aplicar la operación Hadamard, $H|ψ_2〉=|ψ_3〉$ se obtiene: $${|ψ_3〉 =|1〉 {(|f(0)〉 - |1⊕f(0)〉)\over \sqrt{2} } }$$ Veamos uno a uno las opciones de este resultado del Caso $2$, cuando $f(0)≠f(1)$. Claramente Nótese que al ser $f(0)\neq f(1)$, en ambos valores de $f(x)$ la resultante de $f(0)⊕f(1)$ es $1$. En efecto, si $f(0)=0$ entonces $f(1)=1$. Esto implica que la suma modulo $2$ es $f(0)⊕f(1)=0⊕1=1$. Así mismo, si $f(0)=1$ entonces $f(1)=0$. Esto implica que la suma modulo $2$ es $f(0)⊕f(1)=1⊕0=1$.
Del desarrollo de los Casos $1$ y $2$ se puede deducir que la función $f$ es constante cuando $q[1]=|0〉$ y es balanceada cuando
$q[1]=|1〉$. Una simple medición sobre q[1] será suficiente para completar la tarea.
 Diagrama de Árbol $U_f$: Casos y Alternativas de $|\psi_3〉$
Un enfoque para la comprensión de los pasos de la operación, es expresar el resultado de $|ψ_3〉$, - que se obtuvo en los Casos $1$ y $2$ -, en términos generales con una fórmula compacta del circuito:
Nótese que el exponente del factor $(-1)$ es $f(x)$, el cual puede ser $0$ ó $1$. Eso implica que el signo positivo o negativo de la expresión $[6]$, depende del valor que tome $f(x)$. $$(-1)^{f(x)} = \begin{cases} (-1)^{0} & \text{Si $f(x)=0$} \\[2ex] (-1)^{1} & \text{Si $f(x)=1$} \end{cases} $$ Sintetizando estos resultados intermedios, a fin de describir $[6]$, se tiene: $$|ψ_3〉 = \begin{cases} \pm |0〉\Biggl(({(|0〉 - |1〉)\over \sqrt{2}})\Biggr) & \text{Si $f(0)=f(1)$} \\[2ex] \pm|1〉\Biggl(({(|0〉 - |1〉)\over \sqrt{2}})\Biggr) & \text{Si $f(0)\neq f(1)$} \end{cases} $$ Ahora, rematando el proceso desarrollado, tenemos el resultado de la operación $f(0)⊕f(1)$ como única medida que puede responder cuando una función es constante o no:
Descripción Circuito Algoritmo de Deutsch Siguiendo la pauta que se ha utilizado a lo largo del presente artículo, para ilustrar gráficamente los circuitos cuánticos con IBM Quantum Experience83, a continuación el Algoritmo de Deutsch y su fuente de código con OPENQASM 2.053, que configura automáticamente la herramienta IBM, una vez simulado o ejecutado el algoritmo del usuario está programando. 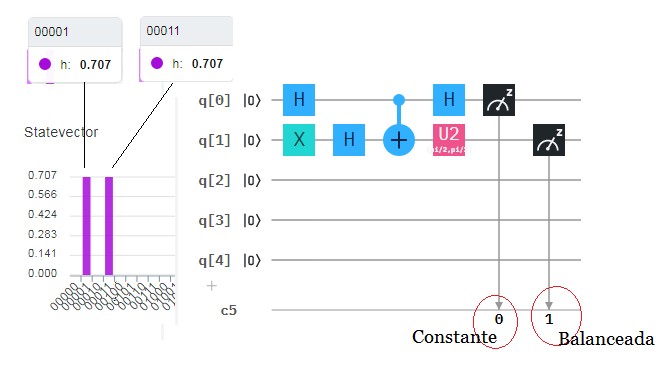 Circuito Versión#1 Algoritmo de Deutsch con el Editor de IBM Pasos Circuito Algoritmo de Deutsch
Ejemplo del Algoritmo de Deutsch en un circuito con otra combinación de $U_f$: 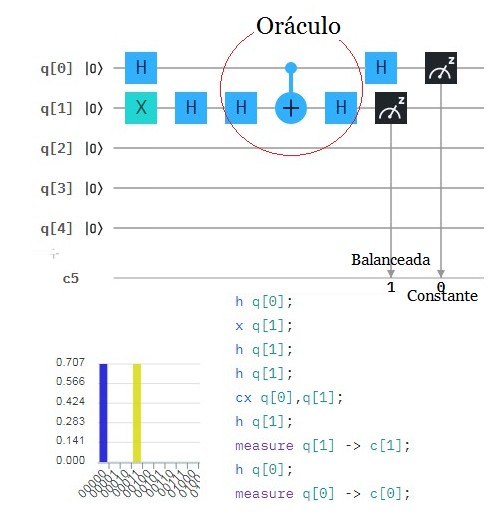 Circuito Versión#2 Algoritmo de Deutsch con el Editor de IBM 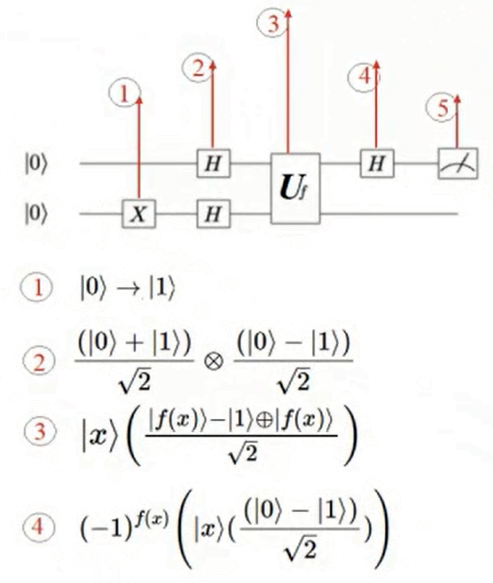 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Otra Descripción del Circuito de la Caja Negra $U_f$ 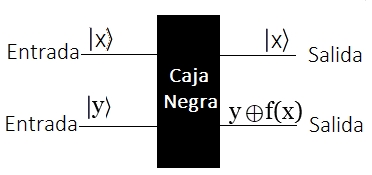 Aquí reiteramos otro enfoque que traduce las cuatro posibles funciones que determinan la caja negra:
Un oráculo $U_f$ o la llamada caja negra que determina si una función es Constante o Balanceada. i) Qubit q[0] es la entrada y qubit q[1] es salida. Ambos inicializados en $|0〉$ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Marco Teórico - Epílogo 
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Notas Complementarias Adjuntas
|
| Buscar: |
|
Expresiones Matemáticas Rotuladas en el Artículo
|
| $[1]$: Expresión Matemática de un Sistema Cuántico |
| $[2]$: Condición que se debe cumplir, a fin que la suma de probabilidades debe ser siempre igual a 1 |
| $[3]$: Expresión Ejemplo Estado Producto que se utiliza para demostrar su factorización |
| $[4]$: Expresión de Bell con Estado Entrelazamiento |
| $[4.1]$: Expresión de Combinación Lineal con Puertas de Pauli de Matriz Unitaria de $2\times2$. |
| $[4.2]$: Deducción del Delta de Kronecker. |
| $[5]$: Transformación Lineal "Oracle"- CNOT Utilizada por Deustch |
| $[6]$: Fórmula compacta del circuito del Alhoritmo de Deutsch |
|
+
Contacto con el Autor
|
| DocIRS © 1988-2026 |


















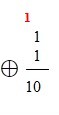
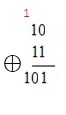
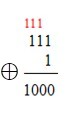
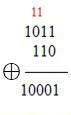
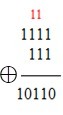
![Objeto que al localizarlo sobre un cable (q[n] hace colapsar dicho circuito](images/medir_small.gif) .
.