|
Breve Introducción
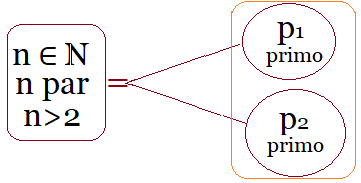
| Todo número par mayor que 2 puede escribirse como suma de dos números primos.
|
Christian Goldbach (1742)
Carta dirigida a Leonard Euler |
La presentación del simulador y breve explicación de nuestro algoritmo computacional acerca de la Conjetura de Goldbach, son un anexo que deriva desde un segmento del documento central realizado durante el año 2020: "Conceptos Matemáticos Básicos de Computación Cuántica".
Hasta hoy esta proposición de Goldbach sigue siendo una conjetura a demostrar. Según el matemático británico Godfrey Harold Hardy en 1921 dijo que "probablemente es una de conjeturas no resueltas más difíciles de la Teoría de Números".
Así mismo, oficial y publicamente durante los tres últimos siglos nadie ha sido capaz de demostrar la conjetura de Goldbach, que aparenta ser sencillo y que muchos audaces matemáticos se han aventurado a lograrlo. Existe una variante de la conjetura llamada débil que fue demostrada, pero no es la misma que se trata en este artículo1.
Igual se debe declarar que existen muchísimas demostraciones que están publicadas y múltiples de ellas disponibles en Internet2. No obstante, según mi entender son demostraciones de caracter heurístico. Porque formalmente en matemática, para que la conjetura se transforme en un teorema, se debe englobar el conjunto infinito de todos los números pares mayores que dos en forma genérica (i.e. demostrarlo $\forall n\in N|n>2 \land n \text{ es par}$).
Quizás estamos con un problema a demostrar tan difícil como el Teorema de Fermat, pero en la Conjetura de Goldbach existen algunas pistas seductoras (que las voy a nombrar más adelante) que invitan a pensar erróneamente que su demostración no sería tan difícil.
|
Pierre de Fermat:
Si $n$ es un número entero mayor o igual que $3$, entonces no existen números enteros positivos $x, y , z$ tales que cumplan con la igualdad:
$$x^{n}+y^{n}=z^{n}\qquad \text{, donde } \unicode{123}x,y,z,n \in Z^{+}\quad \land \quad n \ge 3\unicode{125}$$
Este teorema fue formulado por Pierre de Fermat en 1637, pero no fue demostrado hasta 1995 por Andrew Wiles ayudado por el matemático Richard Taylor. La búsqueda de una demostración estimuló el desarrollo de la teoría algebraica de números en el siglo XIX y la demostración del teorema de la modularidad en el siglo XX.
|
Nota Acerca del Teorema de Fermat
Sin embargo, introducirse en el desafío de comenzar a probar la Conjetura de Goldbach, nos puede llevar por unos laberintos inesperados del universo actual y futuro de las matemáticas, y pasar lo mismo o peor de lo que le sucedió al gran matemático Andrew J. Wiles, quien estuvo varios años de su vida dedicado para lograr demostrar el último teorema de Fermat.
La recompensa de Andrew J. Wiles no sólo fue el Premio Abel (considerado como el "Premio Nobel de las Matemáticas"), sino superar un anhelo que se había propuesto desde niño, y alcanzar la proeza que no había logrado ningún gran matemático por más de 350 años de búsqueda.
Bueno, todos los amantes de las matemáticas esperamos que en algún momento aparezca un científico como Andrew J. Wiles, que demuestre que no existe un número par que no pueda descomponerse como la suma de dos números primos.
Volviendo a la conjetura de Golbach, las pistas más relevantes,- según mi parecer-, son por ejemplo:
i) Todo número primo mayor que $2$ es impar.
ii) La suma de dos números impares es siempre par.
De mi parte, por el momento sólo ofrezco el siguiente algoritmo computacional- que obviamente no es una demostración formal matemática-, sino sólo un desarrollo computacional que confirma la conjetura3, para cada vez que el usuario ingresa un número entero par.
El algoritmo opera sus tiempos de respuesta según la capacidad del ordenador sea clásico o cuántico.
En el este caso, - el simulador publicado con el que se comienza el presente artículo-, se limitó la magnitud de la entrada a un número par de hasta 12 dígitos. (Digamos hasta $999999999998 = 499999997257+500000002741$, lo que toma unos segundos de ejecución). Obviamente, deben existir algoritmos y desarrollos computacionales más óptimos para probar esta conjetura de Goldbach.4
En esta propuesta, el usuario ingresa un número par mayor que $2$ o selecciona un número aleatorio presionando el botón  y ejecuta. El sistema opera el conjunto $U_f$ de funciones, toma el parámetro y devuelve los dos sumandos que primero encuentre5 que configuran la suma del número dado. (Ver simulador al inicio)
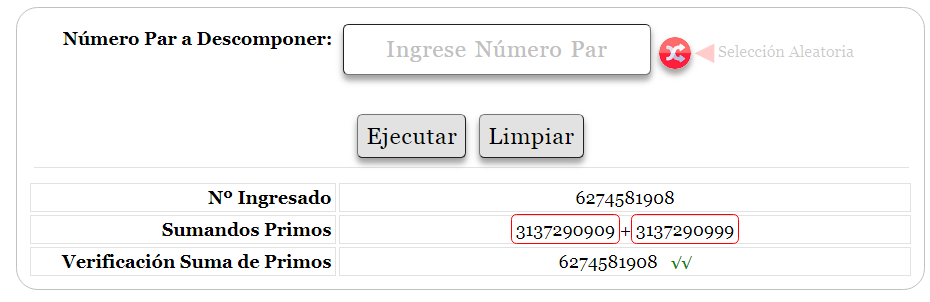
Vista del Simulador
Algoritmo Propuesto y Javascript
Entonces, sea $x\in\unicode{123}x\in Z|\text{x es par } \land x>2\unicode{125}$ y sean $y_1,y_2$ dos enteros primos, que asumimos como los sumandos de $x$, i.e. $x\longrightarrow U_f \longrightarrow x=y_1 + y_2$.5
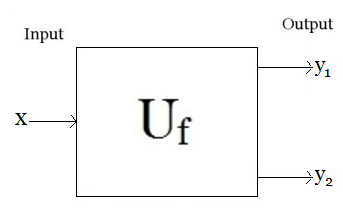
Luego, el algoritmo $U_f$ lo conformaremos por las siguientes funciones en javascript:
- IsEntero(x) : Se le pasa un número como parámetro y responde con falso ó verdadero si es un número entero o no.
Es decir, esta función auxiliar es invocada por GoldBacht(x) para validar que el número de entrada al algoritmo sea un entero.
- IsPar(x) : Se le pasa un entero como parámetro y responde con falso ó verdadero si es par o no. Es decir, esta función valida que el número entero de entrada cumpla con el enunciado de Goldbach, el cual se refiere a la descomposición de un entero par en dos números primos.
Nótese que todo número par mayor que $2$, se puede descomponer en dos sumando impares. En efecto, si se toman dos enteros impares de la forma $2n +1$ y $2m+1$, con $n,m \in N$ y se suman, se obtiene la siguiente expresión: $(2n +1) + (2m+1)=2n + 2m + 2 = 2(n + m + 1)\Rightarrow$ que la suma es par.
- IsPrimo(x) : Se le pasa un entero como parámetro y responde con falso ó verdadero si es primo o no.
Esta función auxiliar juega el rol importante, se utiliza en rutina central GoldBacht(x), para validar la proposición lógica que determina si los sumandos $y_1 \land y_2$ son primos, dentro del loop. Al ser simultáneamente ambos primos, la proposición es verdadera saliendo del condicional y del loop.
- Goldbach(x): Se le pasa un entero $x$ como parámetro,- se valida por las funciones anteriores -, y devuelve los dos sumandos primos $y_1 \land y_2$, cuya suma es el parámetro ingresado $x$.
El proceso de esta función central Goldbach(x) del Algoritmo $U_f$, opera abriendo un loop que toma el valor ingresado $x$ y lo divide en 2, (sin decimales), cuadrando los dos valores resultantes para que se mantenga el entero par ingresado. Si no se cumple la condición, se le suma uno al primer sumando y se le quita uno al segundo. Enseguida, se valida nuevamente si cada uno de estos sumando es primo. Así sucesivamente se va verificando la preposición lógica, hasta que se cumple que ambos sumandos son primos (obviamente se va manteniendo la ecuación igual a $x$). Ahí, se cierra el proceso y se publican los sumandos $y_1 \land y_2$, cuya suma obviamente es $x$
$U_f$: Algoritmo de Goldbach - Conjunto de Funciones Javascript
<script language='javascript'>
/*Conjunto de funciones para describir un algoritmo
para la Conjetura de Goldbach ~ JEGC DocIRS 2021*/
function isEntero(x)
{
if (x === parseInt(x, 10))
return true
else
return false
}
function isPrimo(x)
{
if(isNaN(x) || !isFinite(x) || x%1 || x<2)
{return false;}
if (x%2==0) return (x==2);
var m=Math.sqrt(x);
for (var i=3;i<=m;i+=2) {
if (x%i==0) return false;
}
return true;
}
function isPar(x)
{
if (x%2 == 0)
{return true;}
else
{return false;}
}
function Goldbach(x)
{
if(isEntero(x)==false)
{
alert("Ingrese Número Entero")
return
}
if(isPar(x)==false)
{
alert("Ingrese Número Par")
return
}
if(x<4)
{
alert("Ingrese Número Par Mayor que 2")
return
}
var auxiliar1=parseInt(x/2);
var auxiliar2=parseInt(x/2);
var vBool=false;
do
{
if(isPrimo(auxiliar1)==false || isPrimo(auxiliar2)==false)
{
auxiliar1=auxiliar1-1;
auxiliar2=auxiliar2+1;
}
else
{
var y1= auxiliar1;
var y2= auxiliar2,
vBool=true;
break;
}
}
while (vBool=true);
return("x = " + eval(y1+y2) +" , donde " + " y1=" + y1 + " , y2=" + y2)
}
</script>
|
|
Selección Aleatoria
