|
Bit vs. Qubit
Superposición-Simuladores Reales y Complejos
Conceptos Matemáticos Básicos de Computación Cuántica

José Enrique González Cornejo
v.7.3/Marzo 2020
|
I. Computación Clásica versus Computación Cuántica El bit (Binary Digit) es la unidad mínima de información empleada en informática, que se expresa por dos posibles estados $0$ y $1$. Con esta base binaria se hace uso directo del almacenamiento primario de datos. 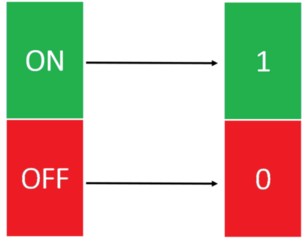
Representación Bit: Binary Digit
Es muy importante en esta comparación tener presente, que en el estado que está el bit es el estado que observamos del bit. 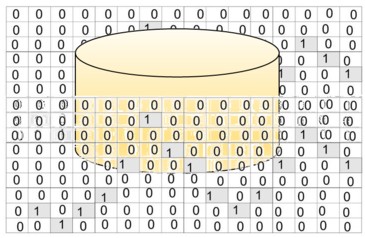
Representación Almacenamiento de Numeración Binaria Sobre esta unidad básica de información, llamada bit se basa la computación clásica. A continuación se ilustra una interfaz, - que contiene un algoritmo-, que transforma números decimales a su equivalente binario. (Ver Algoritmo para el Cambio de Base Numérica (en $n \in \mathbb N$)) |
| Decimal/Base | |
Ingrese Número |
|
| Entero Decimal | Equivalente Base | |||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
La unidad básica de la información cuántica es el qubit. Un qubit corresponde a un sistema físico que
tiene dos estados ortogonales, que denotamos de acuerdo a la Notación de Dirac1 como:
$|0〉$ y $|1〉$. Los estados del sistema, que denotamos $|ψ〉$ se denominan kets.
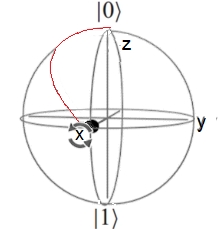
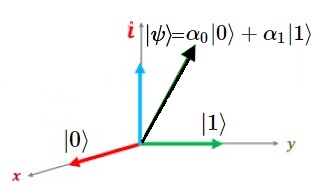 Dirac: Representación de Estados Ortogonales
Estos estados no vacíos se tratan como vectores de base2. Es decir, se aplica una correspondencia hacia una estructura algebraica de Espacio Vectorial.
Espacio Vectorial - Notación Dirac Los qubits se tratan dentro de un Espacio Vectorial Complejo3 y se determina que por las clásicas 8 propiedades fundamentales:
Superposición
Por tanto, un qubit puede también encontrarse en una Superposición de los estados $|1〉$ y $|0〉$. Es decir, como una combinación lineal de los vectores de base, de la forma:
$\alpha_0|0〉+\alpha_1|1〉$. Estos coeficientes $α_i$, son denominados amplitud de probabilidad4, los cuales son números complejos que se utilizan para describir el comportamiento del sistema. La suma del cuadrado de cada uno de esos módulos,- ($|α_0|^{2} + |α_1|^{2} = 1$) -, representa una probabilidad o densidad de probabilidad. Es decir, estos coeficientes $α_i$ son de la forma $z = x + iy$, donde $i = \sqrt{-1}$.
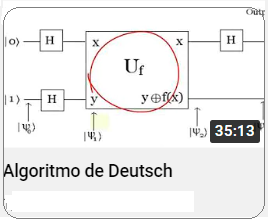
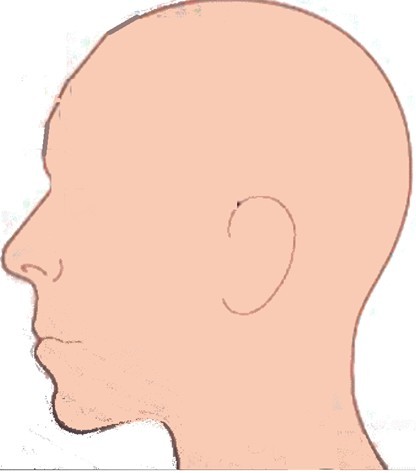
 Representación de un Atomo sin Medirlo Esta unidad básica de información cuántica que se denomina qubit, se verá de similar a un bit, pero a medida que avanzamos veremos que son fundamentalmente diferentes y que esta diferencia permitirá hacer un procesamiento de información nuevo y muchísimo más potente. Por ejemplo, se probó que dada una función $f(x)$, un algoritmo cuántico es capaz de evaluar la función en múltiples valores de $x$ simultáneamente. (Esto no es posible en el sistema tradicional con bits. (Ver Desarrollo Algoritmo de Deutsch Desde ya, la diferencia con el bit en cuanto al almacenamiento es enorme5, dado que el estado de un qubit en Mecánica Cuántica representa niveles de energía de una partícula subatómica y por tanto su almacenamiento físico es en un dispositivo atómico, el cual permite utilizar los múltiples estados en forma simultánea. Es ahí entonces, donde se van guardando los estados intermedios que adquiere el qubit. De igual modo, la capacidad de ambas unidades básicas de información independientemente de la velocidad, son cuantitativamente diferentes. En efecto, el número de estados que se alcanza al introducir un qubit es exponencial, a diferencia de los estados que se alcanza al introducir un bit. En computación clásica se trabaja con $n$ bits y si se aumenta en un bit, el cambio es a $n+1$ estados de almacenamiento. Es decir, la capacidad de medición física del bit es lineal. 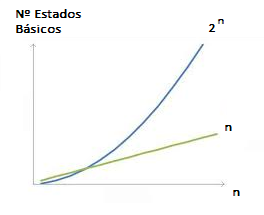
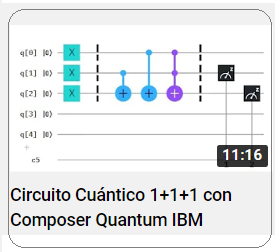
Comportamiento Lineal vs Exponencial En contraste, en un sistema cuántico si se trabaja con $n$ qubits, al aumentar en $1$ qubit se duplica la información que almacena el estado interno ($2·2^{n} = 2 ^{n+1}$). Es decir, el incremento del número de qubits tiene un efecto de medición física exponencial sobre el número de estados o vectores. Sin contar con los estados en superposición del qubit, que pueden ser infinitos. Un qubit está sometido a una variabilidad continua dentro del conjunto de estados cuánticos. Al medir ese estado en movimiento, el sistema determinísticamente asume un estado único. Es decir, el proceso de medición le produce un colapso al estado en superposición y converge a uno de esos estados cuánticos. (Ver Medir una Superposición)  Representación de un Atomo Colapsado (Medido) La relación entre el número de qubits $n \ge 1$ y el número de estados o vectores $m=2^{n}$ define el poder del computador cuántico y la posibilidad de codificar su evolución. Dado que al medir el sistema en superposición, se tiene un número exponencial de estados determinísticos, donde el sistema, - bajo cierta probabilidad_, colapsará a uno de ellos. Más adelante, se mostrará algebraicamente, que los estados cuánticos de qubits múltiples son un producto tensorial de la base canónica {$|0〉,|1〉$}.(ver Estado de Múltiples Qubits) Por ejemplo con $n=2$ bits, se opera con $2$ estados básicos $|01〉,|10〉$. Mientras que con $n=2$ se cuentan $4$ estados básicos $|00〉,|01〉,|01〉,|11〉$, y con $3$ qubits 8 estados, $4$ qubits 16 estados,...y la serie en potencias de $2$ continúa así sucesivamente. (Ver Eligir Nº Qubits - Simular Amplitudes Aleatoriamente.)
En el párrafo de paralelismo cuántico, - más adelante-, veremos que uno de los efectos más significativos de la aplicación de la superposición cuántica dentro de un algoritmo, justamente se basa en el hecho de poder realizar múltiples operaciones sobre un mismo estado cuántico.
  Maurits Cornelis Escher: Peces y Pájaros Puesto en Superposición sobre Colores Obviamente, esta propiedad implica un tremendo incremento en la capacidad computacional, dado que se computan secuencias de transformaciones unitarias simultáneas por cada elemento en superposición, generando un procesamiento masivo de datos paralelos. 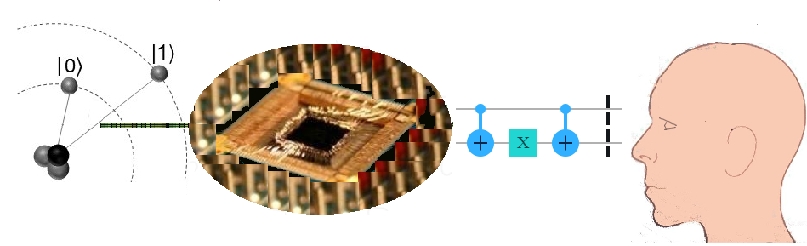
Nanotecnología, Microelectrónica, Lenguajes conectan al mundo cuántico
Es decir, para darnos una idea tomemos un número aleatorio cualquiera $\alpha \in R ,\quad$ tal que $0 < \alpha < 1$. Entonces la posición del estado básico $|0〉$ tiene la amplitud de probabilidad $\sqrt{\alpha}$ y en la posición del estado básico $|1〉$ la amplitud de probabilidad $\sqrt{1-\alpha}$.
|
||||||||||||||||||||
|
Ejemplo Estado Superposición: Si tenemos el siguiente ket:
y se verifica que $|α_0|^{2} + |α_1|^{2} = 1$, entonces $α_0$ y $α_1$ son amplitudes de probabilidad compleja. De modo que, si $|\alpha_0|^{2}=0.4$ y $|\alpha_1|^{2}=0.6$, esto implica que existe la probabilidad en un 40% de colapsar hacia $|0〉$ y del 60% de que el qubit pudiese colapsar a $|1〉$.
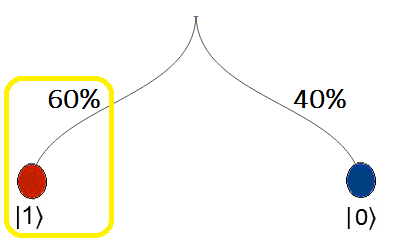
Decimos colapsar, dado que al momento de observar o Medir una superposición8, el sistema sólo permite mostrar uno de los dos estados básicos $|0〉$ o $|1〉$.
Es decir, va a colapsar a uno de los estados básicos dependiendo de la distribución de probabilidad que tenga en ese instante. Considerando que en cada micro-nano-segundo de tiempo, el qubit se encuentra en una superposición de estos estados.
|
||||||||||||||||||||
 |
← | ||
|
Mientras gira la moneda no es posible determinar el estado en que se encuentra.  Infinitos Estados en Superposición
En computación cuántica el sistema puede ser manipulable en su evolución12. Sin embargo, existe un obstáculo aún hoy, en cuanto al almacenamiento. El problema de los estados cuánticos que forman los qubits es que son muy frágiles, y colapsan en cuestión de nanosegundos.
13
$$\psi = \sum_{i=0}^{n-1} u_i |i〉\qquad\qquad [1]$$ Donde los $u_i \in C$ son las amplitudes de probabilidad normalizadas (Ver Amplitudes de Probabilidad con Números Complejos), i.e. $$\sum_{i=0}^{n-1} |u_i^{2}| = 1 \qquad\qquad [2]$$ Estado de Múltiples Qubits
La notación de Dirac incluye una operación llamada producto tensorial, denotada como $⊗$. Esto es importante porque en la computación cuántica, un vector de múltiples qubits, es posible descomponerlo como producto tensorial de los dos vectores de estado básico (Ver Estado Producto).
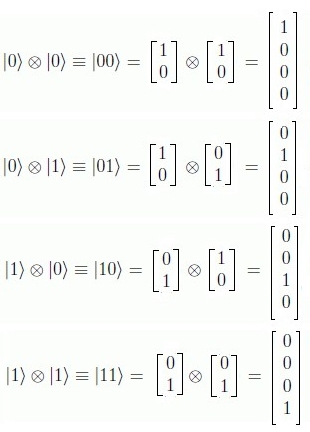 Si definimos dos espacios complejos de dimensión finita $V$ y $W$ de dimensiones $n$ y $m$ respectivamente, en el espacio de Hilbert, con sus bases ortonormales: {$v_i$}$_{i=0}^{n-1}\quad$ y $\quad${$w_j$}$_{j=0}^{m-1}$
Entonces el producto tensorial entre $V⊗W$, es un espacio que tiene como base:
$\Rightarrow$ $$Dim(V⊗W)=Dim(V)⊗Dim(W)$$ Atención por que existen vectores en el espacio complejo unitario que no se pueden expresar como producto tensorial de estados básicos. Estos estados se dicen que están entrelazados.(Estado de Entrelazamiento Cuántico)
En efecto, podemos extender la notación a varios qubits y configurar matemáticamente un sistema cuántico. A continuación se verá que cuando se trata de múltiples qubits, el número de vectores o de estados que se incorporan a la combinación lineal. Si $n$ es el número de qubits entonces los estados que se generan son $2^{n}$, dado que responde a la cantidad de combinaciones que se configuran con los estados básicos {$|0〉, |1〉$}.
El simulador permite seleccionar el número de qubits (1 a 5), utilizando el listbox. Los cálculos de las amplitudes de probabilidad $\alpha_i$ se van generando dinámicamente. Del mismo modo, más abajo se publica la variación del estado cuántico del ket $|\psi〉$ y el cumplimiento de la regla de densidad de probabilidad ($|α_0|^{2} + |α_1|^{2} = 1$). Al momento de presionar el botón Medir, el sistema va colapsar mostrando el resultado. También admite visualizarlo en una gráfica de barras con la distribución del instante. Para poner en marcha nuevamente el sistema basta con presionar el botón Superponer y continuar probando.
|
||||||||||||
|
En la simulación antes descrita, se muestra el cálculo, - en forma dinámica-, de los múltiples coeficientes (o amplitudes) de los qubits en los números Reales, a fin de que la suma de sus normas al cuadrado sea igual a $1$.
El algoritmo cuántico va almacenando información de la superposición de los estados que se están generando, los cuales son manipulados mediante transformaciones unitarias. En cierto instante, se colapsa el sistema para extraer información útil del ket $|\psi〉$ resultante.
i) Tomando un conjunto de $2^{n}$ de valores aleatorios en el intervalo $]0,1[⊂R$ ii) Se normalizan (para que su sumatoria sea igual a 1; ii) Se extrae la raíz cuadrada de cada uno de ellos, de ese modo que ese conjunto de valores, - sean negativos o positivos-, al elevarlos al cuadrado sumen $1$.
Mientras más qubits maneje un procesador cuántico, la potencia de cálculo es de magnitud astronómica. Los experimentos de cálculo realizados hasta hoy con estos aparatos, son capaces de manejar y calcular en segundos estimaciones que en un computador normal demoraría 10.000 años.
Ejemplo de normalización con números aleatorios Reales: Tomemos arbitrariamente un conjunto con cuatro valores {$0.34, 0.56 , 0.48, 0.67$} ($α_i$=Math.random). Entonces,
La normalización significa que cada uno de los valores reales aleatorios del conjunto {$0.34, 0.56 , 0.48, 0.67$}, se divide por su suma $Σ|α_i| = 2.05$ (Ver primera columna de la tabla).
Formalizando el ejemplo,(aplicando $[1]$):
Dado un $n∈\mathbb{N}$. Sea $m=2^{n}$, entonces el conjunto $A =${$α_1, α_2, α_3,...., α_m$} de $m$ valores seleccionados aleatoriamente, tal que $Σ|α_i|^{2} = 1$ , donde cada $α_i ∈R$ y $0< α_i< 1$ , con $i = 1,2,3,..m$. Se determina, - en este ejemplo en particular-, con las siguientes funciones en javascript:
Matriz de $\quad 2^{2} \times 2^{2}\quad =\quad$4 $\times$ 4
Coeficientes Complejos
El hecho de que las probabilidades deben sumar uno, pone algunas restricciones sobre lo que pueden ser los coeficientes o amplitudes en la combinación lineal:
Y dado que los cuadrados de estos coeficientes $α$ y $β$ están relacionados con la probabilidad de obtener un resultado de medición, ellos están limitados por el requisito:
De modo que cuando esta condición es satisfactoria para los cuadrados de los coeficientes de un qubit, se dice que el qubit está
normalizado y admite calcular el módulo de estos números de la siguiente manera 16 :
$|β|^{2}=ββ^{*}$ Donde $α^{*}$ es el complejo conjugado de $α$ y $β^{*}$ es el complejo conjugado de $β$. Es decir, si $z = x + iy$ , entonces el conjugado es $z^{*} = x - iy$, donde $x, y \in R$. 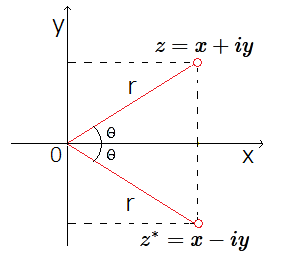 Representación Gráfica de $z$ y $z^{*}$ 17 Por tanto el modulo: |z|2=(x + iy)(x - iy)=x2 + ixy - ixy + y2 $\Rightarrow$ |z|2 =x2 + y2 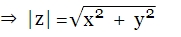
Ejemplos:
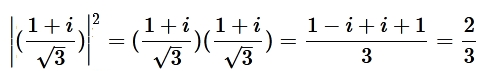 Por tanto, la probabilidad del que el sistema cuántico $|ψ〉$ se encuentre en estado $|0〉$ es $p = \frac {2}{3}$ Obviamente la probabilidad de que $|ψ〉$ se encuentre en estado $|1〉$ es $q = 1 - \frac {2}{3} = \frac {1}{3}$ Función javascript - Normalización
A continuación, el código de una función en javascript para la normalización de un número complejo, ingresado en forma separada su parte real e imaginaria.
Amplitudes de Probabilidad con Números Complejos
En las tablas a continuación se ilustra cómo se normaliza un conjunto de números complejos, a fin de satisfacer el requisito de que la suma de los módulos al cuadrado de las amplitudes de probabilidad de todos los estados posibles es igual a 1.
Nótese que al presionar el botón Medir, colapsa el sistema en el estado básico más probable, de inmediato aparece el botón Superposición que al presionarlo activa la generación de amplitudes de probabilidad dinámicamente y vice versa.
Los coeficientes complejos generados dinámicamente en forma aleatoria en la Tabla#1 se normalizan en $u_i$ en la Tabla#2, y permiten representar el estado de un qubit en superposición. En efecto, valores que pueden describir el comportamiento de un sistema cuántico. El cuadrado del módulo de esta cantidad representa una probabilidad o densidad de probabilidad. La cantidad de $2^{n}$ coeficientes generados se realiza en función del número $n$ de qubits que se está operando.
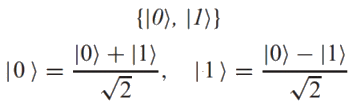
Dada una base ortonormal, cualquier estado puro $|ψ〉$ de los vectores $|0〉$ y $|1〉$ de un sistema cuántico de dos niveles se puede escribir como una superposición de los vectores base, donde el coeficiente o la amplitud de cada vector base es un número complejo. Sin embargo, dado que sólo la fase relativa entre los coeficientes de los dos vectores básicos tiene algún significado físico, podemos tomar el coeficiente de $|0〉$ como real y no negativo.
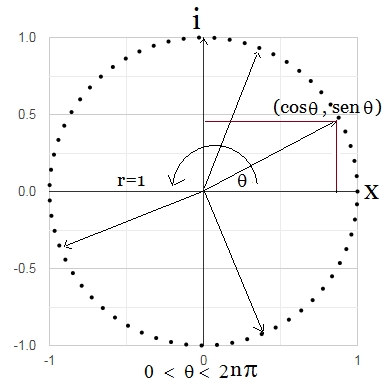
Nótese que al normalizar un número complejo $z$ en su forma polar o bajo la fórmula de Euler18 $$u = e^{iΘ}=cosΘ + i·senΘ$$ nos aseguramos que $$|u|^{2}=cos^{2}Θ + sen^{2}Θ=1$$
Es decir, que la suma de los módulos al cuadrado de las amplitudes de probabilidad de todos los estados posibles es igual a 1.
Bit vs. Qubit Conceptos Matemáticos Básicos de Computación Cuántica 
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|