Distancia Punto a una Recta~Sustentación del Modelo ~

Distancia de un Punto a una Recta

Sustentación del Modelo
Complemento de Conceptos Matemáticos

José Enrique González Cornejo
Enero del 2012

Demostración de la fórmula $[1A]$ utilizada en Sustentación del Modelo Complemento de Conceptos Matemáticos, para los Mínimos Cuadrados

Demostraremos en el plano cartesiano, i.e. dimensión $n=2$, con un enfoque geométrico. Luego, dados un punto $P(x_i,y_i)$ y la ecuación de la recta $y = mx +b$, donde los valores $m,b\in R$ son la pendiente y el corte o intercepto $b$ en el eje $y$ de las abscisas respectivamente. Entonces, se demostrará que la distancia $d_i$ más corta del punto $P$ a la recta $L$ es:

$$ d_i=\frac{|mx_i-y_i + b|}{\sqrt{m^{2}+1}} $$ $$ \qquad\qquad [1A] $$

Es decir, $d_i$ es la longitud del segmento perpendicular a la recta $L$, trazada desde el punto $P$.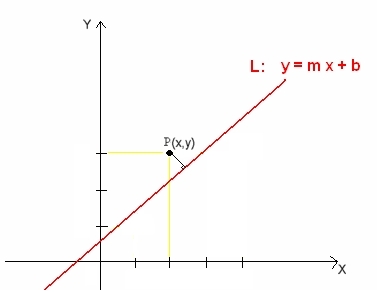

Figura 1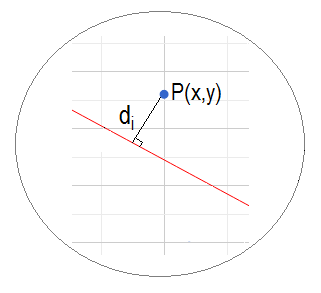

Figura 2

En efecto, proyectemos algunas líneas hacia los ejes y rotulemos los puntos y ángulos necesarios, tal como se ilustra en la figura siguiente. Desde ahí, veremos que la hipotenusa del triángulo superior $d_i$ se puede expresar en función de los datos dados en el enunciado. Es decir, si obtenemos el $\sin(\beta)$ podemos calcular directamente $d_i$.

Figura 3 ~ Distancia Punto a un Recta

Luego, dada la pendiente $m$ de la recta, sabemos que $m= tan(\alpha)$, donde $\alpha$ es el ángulo del triángulo $ABC$:

$$tan(\alpha)=\frac{m}{1}=\frac{k·m}{k},\quad \text{donde }k\in R \text{ / } k\neq0$$

(Recordar que la tangente es igual al cateto opuesto dividido por el adyacente en un triángulo rectángulo. Es decir, en este caso tomamos el triángulo $ABC$ y le asignamos al cateto adyacente $\overline{AC}$ el valor $k$ y al cateteto opuesto $\overline{BC}$ el valor $mk$)

Es decir, la distancia $\overline {BC} = km$ dado que es el cateto opuesto a $\beta$, en el triángulo rectángulo $ABC$, y la hipotenusa es $\overline {AB}=(k·\sqrt{1+m^2})$, entonces:

$$\require{cancel} \sin(\beta)=\frac{\cancel {k}} {\cancel {k}\sqrt{m^{2}+1}}=\frac{1}{\sqrt{m^{2}+1}} $$

(Recordar que el seno es igual al cateto opuesto dividido por la hipotenusa en un triángulo rectángulo)

Dado que $d_i$ es el cateto opuesto a $\beta$ en el triángulo superior $BPD$, tenemos que el segmento $\overline {BP}=|y_i - (mx_i + b)|$ es la hipotenusa de ese triángulo (Ver Figura 3). Por tanto:

$$ d_i= |y_i - (mx_i + b)|· sin(\beta) $$

Sustituyendo $sin(\beta)$, obtenemos la expresión:

$$ d_i=\frac{|y_i - (mx_i + b)|}{\sqrt{1+ m^2}}$$

Expresión que demuestra la fórmula $[1A]$:

$$ d_i=\frac{|mx_i-y_i + b|}{\sqrt{m^{2}+1}} $$

QED

A continuación, se verá un "Scatter plots", de puntos $P_i(x_i,y_i)$ con múltiples distancias $d_i$.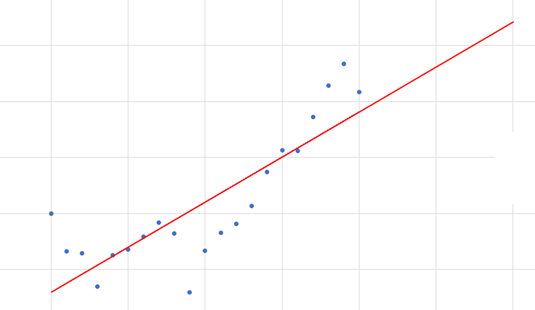

Figura 4
Ver Simulador de Puntos Aleatorios y Ajuste de Curvas ~ Plano Cartesiano