|
Introducción
A continuación desarrollaremos un ejemplo de regresión lineal
múltiple, utilizando datos del Instituto Nacional de Estadísticas
(INE) de Chile, extraídos de Series de Indicadores Excel del Banco
Central de Chile (Ver Datos).
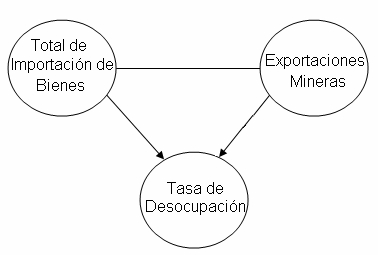
Figura 1
Intencionadamente, hemos buscado variables relacionadas con el
empleo, la exportación minera, y la importación de bienes. La idea
es ilustrar el procedimiento estadístico-matemático y resolución con
Excel, sin mayores pretensiones de establecer una interpretación
económica actualizada de las relaciones que adoptemos.
El supuesto para determinar la ecuación es que existe una relación entre las variables que hemos incluído en el modelo (Ver [R1]). Luego, a partir de las data recolectada en la muestra (Ver Figura 2) se gráficará un diagrama de dispersión sobre el plano cartesiano, de donde se visualizará el ajuste de la curva que aproxime de la mejor forma los datos (Ver Simulador Ajuste de Curvas  ). ).
Nos enfocaremos en la configuración del modelo estadístico-matématico, complementado con dos artículos asociados que son básicos para la comprensión del método de los Mínimos Cuadrados:
Un primer artículo complementario donde se muestran las tendencias de la curva bajo un conjunto de observaciones en el plano, utilizando un simulador gráfico aleatorio con el ajuste de curvas.
"¿Cómo se deduce la fórmula de los coeficientes Mínimos Cuadrados?  " "
Un segundo artículo con una demostración de la deducción de la fórmula que determina la distancia más corta de un punto a la curva en el plano.
"Distancia de un Punto a una Recta  ". ".
Es decir, estimaremos los parámetros de tres variables utilizando el
método de los mínimos cuadrados, explicado en Complemento de
Conceptos Matemáticos ~
Mínimos Cuadrados, a fin de analizar los cambios que operan en
la relación.
Para este efecto, buscamos un tramo de datos de 34 meses
consecutivos, desde marzo del 2009 hasta diciembre del 2011, para la
Tasa de Desocupación (%)[1],
Total Exportaciones Mineras[2]
y el Total de Importación de Bienes (FOB) [3]
en Chile.
Modelo
Analizaremos la variación de la Tasa de Desocupación, explicada por
las variables y Exportaciones Mineras y los Totales de
Importación de Bienes Importación de Bienes durante ese rango de
tiempo.
Sea $Y$ una función general explicada por 2 variables
agregadas, expresada en el siguiente modelo:
$$
Y=\beta_0 + \beta_1 X_1 + \beta_2 X_2 + \mu\qquad\quad [R1]
$$
Donde:
Y: Tasa de Desocupación (%) (Miles de personas);
X1: Total de Importación de Bienes (FOB,Millones de dólares)
X2: Exportaciones Mineras (Millones de dólares);
$\mu$ : Error o Residuo
Cada una de estas variables definida en el periodo t. Donde los coeficientes a estimar son $\beta_0,\beta_1,\beta_2 \in R$. Así mismo el error $\mu \in R$.
Obsérvese, que el parámetro tiempo está implícitamente incorporado,
efectivamente la expresión [R1], formalmente puede tratarse
mediante la siguiente función:
Yt = F(X1t , X2t)
[R2]
Por tanto, determinaremos la función, utilizando un modelo lineal,
con la data de los periodos mensuales desde marzo 2009 hasta marzo 2010. Es decir,
ordenaremos en Series de Tiempo o una secuencia ordenada por año los
valores agregados de las variables que explican la variación de Y.
Donde t es el valor en el mes t de la variable a explicar Y, ß0
es el intercepto o valor inicial en t=0, y $\hat{\beta_1}$ y $\hat{\beta_2}$ son los coeficientes, - a estimar -, que acompañan las
variables explicativas, y $\mu$
el error (o residuos para cuadrar la ecuación [R1]).
Nótese que el supuesto que parte de la variación de la Tasa de
Desocupación se puede analizar mediante los Totales de Importación
de Bienes (X1) y Exportaciones Mineras (X2),
es una hipótesis que utilizamos sólo como ejercicio, para
complementar el procedimiento estadístico de la regresión lineal
múltiple.
El ejercicio utiliza estas
series de tiempo, por la existencia de datos reales que tenemos
sobre estas tres variables.
Por tanto, asumimos que con los datos disponibles y el
método de regresión lineal múltiple es posible estimar los
coeficientes de la ecuación [R1] para que representar la
distribución conjunta de las dos variables incluidas en el modelo.
La proyección Yt+1 agregada y diferenciada se
estimará realizando cambios en las variables explicativas (también
cambiando los niveles de la tasa Yt+1). Por ejemplo,
mantendremos constante el valor promedio del Total de Importación de
Bienes, para estimar en cuánto deben variar las Exportaciones
Mineras para alcanzar un determinado nivel de Tasa de Desocupación.

Figura 2
Sólo por observación del “plotting” de la Figura 2, podemos
concluir que la curva, a estimar mediante el método de los mínimos
cuadrados, tendrá pendiente negativa: También se observa que es
probable que las variables explicativas no sean tan independientes.
Es decir, que exista colinearidad entre X1 y X2
. Nótese que siempre nos hemos referido a estas 2
variables incorporadas al modelo, como explicativas. Es decir, en
ningún momento la hemos mencionado como variables independientes,
dado que este supuesto de independencia es “temerario”, para
no decir falso.
La Data
| |
Tasa de Desocupación (%) |
Total de Importación de Bienes (fob) |
Exportaciones Mineras |
| Año |
Mes |
Y |
X1 |
X2 |
|
2009 |
Marzo |
10,6 |
2,91 |
2,07 |
|
|
Abril |
10,9 |
3,19 |
2,21 |
|
|
Mayo |
11,4 |
2,77 |
2,46 |
|
|
Junio |
11,5 |
3,00 |
2,57 |
|
|
Julio |
11,6 |
3,74 |
2,84 |
|
|
Agosto |
11,6 |
3,25 |
2,83 |
|
|
Septiembre |
11,2 |
3,25 |
2,52 |
|
|
Octubre |
10,7 |
3,89 |
3,79 |
|
|
Noviembre |
10,4 |
4,00 |
3,41 |
|
|
Diciembre |
10,0 |
4,17 |
4,02 |
|
2010 |
Enero |
9,7 |
3,88 |
2,76 |
|
|
Febrero |
9,1 |
3,65 |
3,04 |
|
|
Marzo |
9,0 |
4,21 |
3,51 |
|
|
Abril |
8,6 |
4,26 |
3,13 |
|
|
Mayo |
8,8 |
4,80 |
3,35 |
|
|
Junio |
8,5 |
4,29 |
3,19 |
|
|
Julio |
8,3 |
5,03 |
3,70 |
|
|
Agosto |
8,3 |
5,05 |
3,96 |
|
|
Septiembre |
8,0 |
4,85 |
4,06 |
|
|
Octubre |
7,6 |
5,18 |
4,08 |
|
|
Noviembre |
7,1 |
5,13 |
4,26 |
|
|
Diciembre |
7,1 |
5,26 |
5,32 |
|
2011 |
Enero |
7,3 |
4,82 |
3,78 |
|
|
Febrero |
7,3 |
4,98 |
3,63 |
|
|
Marzo |
7,3 |
6,18 |
4,73 |
|
|
Abril |
7,0 |
5,60 |
4,26 |
|
|
Mayo |
7,2 |
5,99 |
4,36 |
|
|
Junio |
7,2 |
5,86 |
4,25 |
|
|
Julio |
7,5 |
6,13 |
3,74 |
|
|
Agosto |
7,4 |
6,49 |
3,51 |
|
|
Septiembre |
7,4 |
6,37 |
3,95 |
|
|
Octubre |
7,2 |
5,75 |
4,13 |
|
|
Noviembre |
7,1 |
6,42 |
4,05 |
|
|
Diciembre |
6,6 |
6,04 |
4,48 |
Tabla 1
El Cálculo
Figura 3
El Resultado
|
Resumen |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Estadísticas de la regresión |
|
|
|
|
|
|
|
|
Coeficiente de correlación múltiple |
0,9121 |
|
|
|
|
|
|
|
|
Coeficiente de determinación R^2 |
0,8320 |
|
|
|
|
|
|
|
|
R^2 ajustado |
0,8212 |
|
|
|
|
|
|
|
|
Error típico |
0,7021 |
|
|
|
|
|
|
|
|
Observaciones |
34,0000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Análisis de Varianza |
|
|
|
|
|
|
|
|
|
Grados de libertad |
Suma de cuadrados |
Promedio de los cuadrados |
F |
Valor crítico de F |
|
|
|
|
Regresión |
2 |
75,6924 |
37,8462 |
76,7664 |
0,0000 |
|
|
|
|
Residuos |
31 |
15,2832 |
0,4930 |
|
|
|
|
|
|
Total |
33 |
90,9756 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Coeficientes |
Error típico |
Estadístico t |
Probabilidad |
Inferior 95% |
Superior 95% |
Inferior 95,0% |
Superior 95,0% |
|
Intercepción |
15,5129 |
0,5979 |
25,9459 |
0,0000 |
14,2935 |
16,7323 |
14,2935 |
16,7323 |
|
Variable X 1 |
-1,0582 |
0,1807 |
-5,8562 |
0,0000 |
-1,4268 |
-0,6897 |
-1,4268 |
-0,6897 |
|
Variable X 2 |
-0,5019 |
0,2700 |
-1,8592 |
0,0725 |
-1,0525 |
0,0487 |
-1,0525 |
0,0487 |
|
|
|
|
|
|
|
|
|
|
Tabla 3 ~ Resultados Y=F(X1, X2)
Análisis de Resultados
|
$$\hat{Y}=\hat{\beta_0} + \hat{\beta_1}X_1 + \hat{\beta_2} X_2$$
|
15,5129 - 1,0582 $X_1$
- 0,5019 $X_2$ |
|
|
(0,5979)
(0,1807)
(0,2700)
|
R2 = 0,8212
|
Donde los valores entre
paréntesis son los errores estándar de los coeficientes estimados.
La interpretación de la
resultante de la regresión es la siguiente:
i) Para el período de la muestra, cuando ambas variables
explicativas son cero (al momento inicial), entonces la Tasa de
Desocupación (Y) es de alrededor de 15,51%. No necesariamente el
intercepto tiene significado económico.
ii) El coeficiente parcial -1,0582 que acompaña a la variable Importación de
Bienes (X1), significa que su efecto es negativo sobre la
variación de la Tasa de Desocupación (Y). Es decir, si crece
en una unidad la importación de bienes, la tasa de desocupación
decrece en aproximadamente 1,1%. A la inversa, si disminuye en una
unidad la Tasa de Desocupación aumenta en alrededor de 1.1% en el
periodo.
El coeficiente parcial -0,5019
que acompaña a la variable Exportaciones
Mineras (X2) sobre el periodo marzo 2009 – marzo 2011,
tiene un efecto negativo sobre la Tasa de Desocupación (Y) en un
0.5%.
iv) El Coeficiente de Determinación R2, significa que
ambas variables X1 y X2 explican la variación
de la Tasa de Desocupación (Y) en 82% .
v) A si mismo, existe una 18% inexplicado que se le atribuye al error μ
En términos de las expectativas a priori, ambas variables
explicativas tienen el signo esperado.
Sin embargo, es para cuestionarse la colinearidad de las variables
explicativas introducidas al modelo, dado que el coeficiente de
correlación es muy alto.
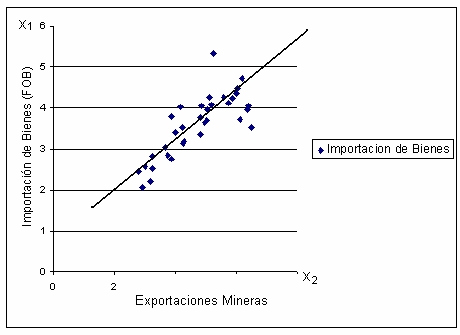
Figura 4
Del diagrama observamos que existe una pendiente positiva y que
tendremos una correlación relativamente alta entre estas variables.
Por tanto, sugerimos regresar X1 versus X2, a
fin de analizar el grado de correlación.
Nótese que le método de regresión lineal no se utiliza sólo para
confirmar hipótesis, sino también para boicotear o rechazar la
hipótesis.
Veamos:
|
$$X_1$$ |
$$X_2$$ |
| 2,91 |
2,07 |
|
3,19 |
2,21 |
|
2,77 |
2,46 |
|
3,00 |
2,57 |
|
3,74 |
2,84 |
|
3,25 |
2,83 |
|
3,25 |
2,52 |
|
3,89 |
3,79 |
|
4,00 |
3,41 |
|
4,17 |
4,02 |
|
3,88 |
2,76 |
|
3,65 |
3,04 |
|
4,21 |
3,51 |
|
4,26 |
3,13 |
|
4,80 |
3,35 |
|
4,29 |
3,19 |
|
5,03 |
3,70 |
|
5,05 |
3,96 |
|
4,85 |
4,06 |
|
5,18 |
4,08 |
|
5,13 |
4,26 |
|
5,26 |
5,32 |
|
4,82 |
3,78 |
|
4,98 |
3,63 |
|
6,18 |
4,73 |
|
5,60 |
4,26 |
|
5,99 |
4,36 |
|
5,86 |
4,25 |
|
6,13 |
3,74 |
|
6,49 |
3,51 |
|
6,37 |
3,95 |
|
5,75 |
4,13 |
|
6,42 |
4,05 |
|
6,04 |
4,48 |
Tabla 4
Aplicando la Regresión del Complemento Análisis de Datos del Excel,
obtenemos:
|
Resumen |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Estadísticas de la regresión |
|
|
|
|
|
|
|
|
Coeficiente de correlación múltiple |
0,80 |
|
|
|
|
|
|
|
|
Coeficiente de determinación R^2 |
0,64 |
|
|
|
|
|
|
|
|
R^2 ajustado |
0,63 |
|
|
|
|
|
|
|
|
Error típico |
0,69 |
|
|
|
|
|
|
|
|
Observaciones |
34,00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ANÁLISIS DE VARIANZA |
|
|
|
|
|
|
|
|
|
|
Grados de libertad |
Suma de cuadrados |
Promedio de los cuadrados |
F |
Valor crítico de F |
|
|
|
|
Regresión |
1,00 |
26,91 |
26,91 |
57,04 |
0,00 |
|
|
|
|
Residuos |
32,00 |
15,10 |
0,47 |
|
|
|
|
|
|
Total |
33,00 |
42,01 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Coeficientes |
Error típico |
Estadístico t |
Probabilidad |
Inferior 95% |
Superior 95% |
Inferior 95,0% |
Superior 95,0% |
|
Intercepción |
0,43 |
0,58 |
0,74 |
0,47 |
-0,75 |
1,61 |
-0,75 |
1,61 |
|
Variable X 1 |
1,20 |
0,16 |
7,55 |
0,00 |
0,87 |
1,52 |
0,87 |
1,52 |
Tabla 5 ~ Resultados X 1 =F(X 2)
Nótese que se estima un
coeficiente ajustado de determinación del 63%, lo que nos señala un
grado de coliniaridad entre las variables X1 y X2,
que no induce a cambiar el Diagrama 1 por el siguiente:
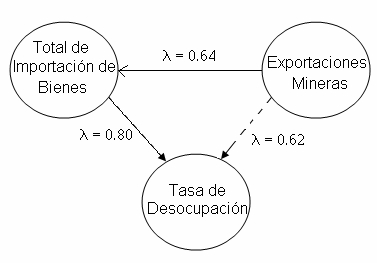
Figura 5
Si se regresa la variable Y con X2 arroja un R2 /sup>Ajustado de 63%. Así mismo si regresa Y con X1 se
obtiene un R2 Ajustado de 80%.
Ambas variables juntas introducidas en el modelo, explican la variación de Y en un 82% (VerTabla 3 ~ R2Ajustado= 0,82)
Proyección
Supongamos se desea disminuir la
Tasa de Desocupación al 6% en un
año, manteniendo constante el Total de las Importaciones de Bienes,
cuyo valor promedio mensual en los 34 meses es de aproximadamente
US$ 4,72 millones entonces ¿En cuánto se debe aumentar las
Exportaciones Mineras?
| Media |
Valor |
Unidad Medida |
|
Y |
8,72
|
% |
|
X1
|
4,72 |
Millones US$ |
|
X2 |
3,58
|
Millones US$ |
Tabla 6
Notas
|