Textos y temas extraídos del documento Conceptos Matemáticos Básicos de Computación Cuántica, a fin de estimar probalísticamente la Amplitud de Probabilidad ⁴ o coeficiente de la Puerta Cuántica de Hadamard.

La tarea es buscar una representación matemática mediante el método de cálculo de aproximación Método de Montecarlo⁵⁹.

Antes, se especificará que el primer postulado de la Teoría Cuántica señala que todo estado de un sistema físico está relacionado con el principio de superposición.

Se repasará el concepto asociado a un qubit corresponde a un sistema físico que tiene dos estados ortogonales, las combinaciones lineales con un simulador aleatorio que genera amplitudes de probabilidad, las propiedades de la transformación unitaria de Hadamard y se finaliza aplicando un modelo de simulación interactivo con el Método de Montecarlo para estimar el coeficiente equiprobable de los vectores de la Base de Hadamard¹⁰⁴.

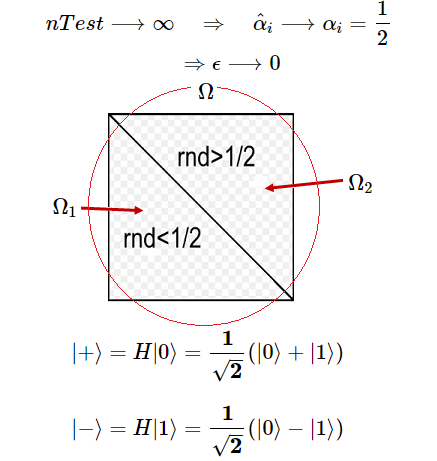Síntesis de la Aproximación

La figura muestra una imagen del simulador, con el cual se cierra y sintetiza el presente artículo. La interfaz contiene un programa computacional con una rutina que mide las amplitudes de probabilidad de los vectores de la Base de Hadamard $\unicode{123}|+〉,|-〉\unicode{125}$, mediante el Método de Montecarlo, a fin de demostrar que se distribuyen equiprobablemente ambos estados.

El simulador permite probar en repetitivas mediciones, - con diferentes números de significativa magnitud de hasta de 100.000.000 de ensayos- , generados por números aleatorios. Aproximando en el límite el comportamiento del coeficiente común ($\frac{1}{\sqrt{2}}$) de los estados básicos de la Puerta de Hadamard. Es decir, el usuario puede calcular aleatoriamente los estimadores $\hat \alpha_1 \text{ y } \hat \alpha_2$ de la combinación lineal $\psi = \alpha_1|0〉+\alpha_2|1〉$, como también el comportamiento de las parámetros asociados y la variabilidad del error. Así mismo, puede observar estos resultados en un tabla dinámica que los va almacenando durante los ensayos.

Se comprobará que este proceso estocástico de secuencias de números aleatorios que se repite en cada ensayo, depende de una secuencia de números que van arrojando resultados diferentes (o no idénticos) durante la simulación. Efectivamente, son secuencias diferentes de números aleatorios. Sin embargo, los valores del resultado de cada ensayo se mantienen acorde y conservan la tendencia.

Introducción

El primer postulado de la Teoría Cuántica señala que todo estado de un sistema físico está representado por un vector de un determinado espacio vectorial, en nuestro caso será el Espacio de Hilbert, - y que este sistema está relacionado con el principio de superposición.

$\longleftarrow$

Medir  Superponer

Para analizar estos sistemas es necesario involucrar todos los aspectos que intervienen en su conformación, junto con el objetivo. De ahí que la tarea es representar matemáticamente elaborando un método de cálculo de aproximación a la fascinante simpleza, que aparenta ser, la equiprobabilidad de los estados cuánticos de Hadamard.

Qubit, Superposición y Hadamard

Un qubit corresponde a un sistema físico que tiene dos estados ortogonales, que denotamos de acuerdo a la Notación de Dirac¹ con los estados básicos $|0〉$ y $|1〉$.

Es decir, un qubit puede también encontrarse en una Superposición de los estados $|0〉$ y $|1〉$, representado como una combinación lineal de los vectores de base, de la forma:

$$\psi = \alpha_1|0〉+\alpha_2|1〉\qquad\quad[A]$$
Estos coeficientes $\alpha_1$ y $\alpha_2$, son denominados amplitud de probabilidad, los cuales son números complejos que se utilizan para describir el comportamiento del sistema. La suma del cuadrado de cada uno de esos módulos, representa una probabilidad o densidad de probabilidad, determinados por el postulado siguiente:

$$|\alpha_1|^{2} + |\alpha_2|^{2}=1\qquad\quad[B]$$
La Puerta de Hadamard simplemente aplica la densidad de probabilidad $[B]$ de forma que sus estados son equiprobables. Hadamard es la transformación unitaria,- que yo llamaría el símbolo de las superposiciones -, que actúa sobre un único qubit.

$$(\frac {1}{\sqrt{2}})^{2} + (\frac {1}{\sqrt{2}})^{{2}}=1\qquad$$
y el estado cuántico

$$\psi =\frac {1}{\sqrt{2}}|0〉 ± \frac {1}{\sqrt{2}}|1〉\qquad $$
Es decir,

$$ H|x〉= \begin{cases} \frac {1}{\sqrt{2}}(|0〉+|1〉), & \text{ (+) } x=0 \\ \frac {1}{\sqrt{2}}(|0〉-|1〉), & \text{ (-) } x=1 \end{cases} $$

La transformación unitaria de Hadamard es un objeto prácticamente ineludible en los algoritmos cuánticos y en la programación de sus circuitos.

En efecto, al aplicar el operador $H$ produce que un qubit pase de un estado básico, $|0〉$ o $|1〉$, a un estado de superposición equiprobable de ambos estados.

Ahora, si se aplica $H$ a un conjunto de varios qubits se logra que el sistema también entre en un estado de superposición equiprobable de todos los estados propios del sistema cuántico. En programación cuántica, cuando se configuran circuitos con puertas cuánticas y se ejecutan múltiples veces (que es lo usual), las probabilidades tienden al valor esperado.

Circuito Estado de Bell ~ Entrelazamiento Cuántico ~ 2-qubit

Ya hemos visto, tanto en el documento de base central "Conceptos Matemáticos Básicos de Computación Cuántica" como en sus videos asociados, que cuando comenzamos a construir un algoritmo cuántico, se establece un conjunto de qubits de inicialización en estado cero para cada cable respectivo, preparando el circuito para introducir los estados en superposición equiprobable con la Puerta Cuántica de Hadamard.

	q[0]=0 q[1]=0 q[2]=0 q[3]=0 q[4]=1
Superposición ~ Producto Tensorial de Hadamard	Idea Superposición ~ Producto Tensorial de Hadamard

Nótese que la superposición generada tiene tremenda potencia, dado que las puertas cuánticas de Hadamard en paralelo se multiplican tensorialmente entre ellas.

Justamente esta propiedad de transformar los estados intermedios y procesarlos de manera paralela es lo que marca la diferencia entre la computación clásica y la computación cuántica.

Obviamente, esta propiedad implica un significativo incremento en la capacidad computacional, dado que se computan secuencias de transformaciones unitarias simultáneas por cada elemento en superposición, generando un procesamiento masivo de datos paralelos.

Si se aplica el producto tensorial $⊗$ con $H$ sobre vectores de varios qubits (operador de Walsh-Hadamard), utilizando la notación en $n$, descrita previamente en Modo Numérico de Representar los Vectores Unitarios. Este producto tensorial con Hamadard, se describe mediante la siguiente expresión:

$$H ⊗ H ⊗ H ⊗\cdots H |\underbrace{0 0 0\cdots 0}_{n\text{ veces}}〉=\frac {1}{\sqrt{2^{n}}}\sum_{x=0}^{2n-1} |x〉\\ x\in \unicode{123}0,1,2\cdots ,2n-1\unicode{125}$$   

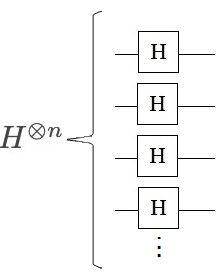La transformada de Hadamard puede considerarse también como construida a partir de transformadas discretas de Fourier.

Mostraremos el Método de Montecarlo, dado que si se visualiza el generador aleatorio de coeficientes que cumplen con las ecuaciones rotuladas previamente con $[A]$ y $[B]$:

Las amplitudes de probabilidad al cuadrado señalan la probabilidad de colapsar hacia el estado básico $|0〉$ o hacia el estado $|1〉$ al momento de medir.

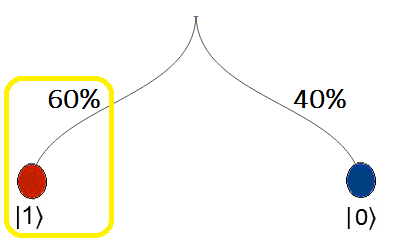
Ejemplo de Colapso a un Estado Básico

$$\alpha_1^{2}\longrightarrow P_r(|0〉)\quad \text{ y }\quad\alpha_2^{2}\longrightarrow P_r(|1〉)$$

Ya sabemos que no es posible observar un qubit en estado de superposición. En el sensible mundo microscópico el observador interviene el sistema. En otras palabras, esto significa que sólo es posible saber el sistema estará en uno de esos probables estados cuando midamos, sin saber con certeza cuál será el resultado

Por eso, primero observemos el comportamiento de un simulador cuyos resultados, después de múltiples mediciones, nos prepara para comprender los estados equiprobables de Hadamard y la aproximación que realizaremos a su coeficiente aplicando el Método de Montecarlo en la parte final del presente artículo.

La propiedad Equiprobable dentro de un espacio muestral, es que todos los elementos que conforman ese universo tienen igual posibililidad de ser elegidos. Es decir, cada elemento tiene la misma probabilidad de ocurrencia.

Eligir Nº Qubits - Simular Amplitudes Aleatoriamente¹⁵

El simulador permite seleccionar el número de qubits (1 a 5), utilizando el listbox. Los cálculos de las amplitudes de probabilidad $\alpha_i$ se van generando dinámicamente. Del mismo modo, más abajo se publica la variación del estado cuántico del ket $|\psi〉$ y el cumplimiento de la regla de densidad de probabilidad ($|α_0|^{2} + |α_1|^{2} = 1$). Al momento de presionar el botón Medir, el sistema va colapsar mostrando el resultado. También admite visualizarlo en una gráfica de barras con la distribución del instante. Para poner en marcha nuevamente el sistema basta con presionar el botón Superponer y continuar probando.

En la simulación antes descrita, se muestra el cálculo, - en forma dinámica-, de los múltiples coeficientes (o amplitudes) de los qubits en los números Reales, a fin de que la suma de sus normas al cuadrado sea igual a $1$.

El algoritmo cuántico va almacenando información de la superposición de los estados que se están generando, los cuales son manipulados mediante transformaciones unitarias. En cierto instante, se colapsa el sistema para extraer información útil del ket $|\psi〉$ resultante.

Este cálculo se realiza de la siguiente forma:

i)   Tomando un conjunto de $2^{n}$ de valores aleatorios en el intervalo $]0,1[⊂R\quad, \text{ donde } n\in N$ es el número de qubits.

ii)   Se normalizan (para que su sumatoria sea igual a 1).

ii)   Se extrae la raíz cuadrada de cada uno de ellos, de ese modo que ese conjunto de valores, - sean negativos o positivos-, al elevarlos al cuadrado sumen $1$.

Puerta Cuántica de Hadamard y Estados Equiprobables

La puerta de Hadamard es muy importante y consecuentemente utilizada en los algoritmos de la computación cuántica, porque se presta para ir aprovechando las ventajas de manejo de la evolución de los estados en superposición, hasta llegar a un lugar que medir esa superposición sea útil para contribuir a solucionar el resultado del algoritmo en cuestión.

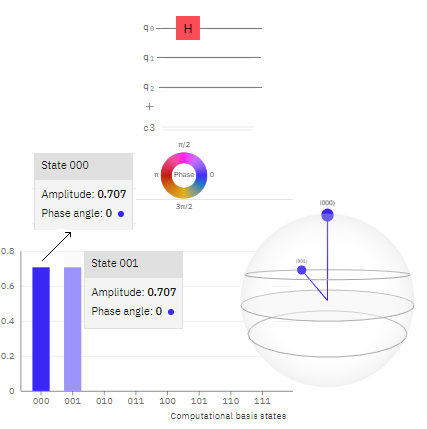IBM Circuit Composer ~ Resultados de $H|0〉$

Hadamard es una puerta de un qubit muy apropiada para generar superposición equiprobable, donde no se favorece ninguno de los estados básicos. Nótese que toma un estado básico de un qubit y lo transforma en un combinación lineal de dos vectores. Es decir, de uno saca dos explicados por el coeficiente común $\frac {1}{\sqrt{2}}$, configurando una superposición equiprobable.

La puerta de Hadamard simplificó la distribución probabilística asignando a las amplitudes de probabilidad de la ecuación $[A]$, exactamente la mitad a cada uno, de modo que cumpliera con el postulado de la ecuación $[B]$. Es decir, aplicar la puerta de Hadamard a cualquiera de los estados básicos devuelve una superposición equiprobable.

La puerta de Hadamard, se puede representar bajo diferentes expresiones matemáticas:

- Definida por la matriz (unitaria): $$ H=\frac {1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \\ \end{pmatrix} $$

- Situando su operación más visual sobre la Esfera de Bloch, con coordenadas polares:

$$ |\psi〉=cos(\frac {\theta}{2})|0〉+ e^{iφ}(\sin(\frac {\theta}{2})|1〉 $$

$H$  ibm quantum experience-fuente gates glossary

Esto implica que se produce una rotación sobre el eje $y$ de un ángulo $\frac{π}{2}$ e inmediatamente otra rotación de un ángulo $π$ sobre $x$. La transformación de Hadamard opera paralelismos masivos. (i.e con $n \in N$ qubits se generan superposiciones de $2^{n}$ estados cuánticos, como combinaciones lineales de $|0〉$ y $|1〉$).

Nótese que al normalizar un número complejo $z$ en su forma polar o bajo la fórmula de Euler¹⁸ $u = e^{iΘ}=cosΘ + i·senΘ$, nos aseguramos que $|u|^{2}=cos^{2}Θ + sen^{2}Θ=1$. Es decir, que la suma de los módulos al cuadrado de las amplitudes de probabilidad de todos los estados posibles es igual a $1$.

Más adelante se verá el capítulo correspondiente a la Transformada Cuántica de Fourier, donde la Puerta Cuántica de Hadamard expresada en coordenadas polares permitirá facilitar la resolución del circuito con el algoritmo de factorización de Shor.

Obsérvese en el documento central, que la Puerta de Hadamard es un combinación lineal de las Transformaciones de Pauli, las que constituyen un Algebra de Lie. (Ver Algebra de Lie ~ Puertas de Pauli).

$$H=\frac{1}{2}(X + Z)$$

La medición de las amplitudes de probabilidad de los vectores de la Base de Hadamard $\unicode{123}+,-\unicode{125}$ mediante el Método de Montecarlo, demuestra que son equiprobables.

$$|+〉=H|0〉=\frac {1}{\sqrt{2}}(|0〉+|1〉)$$
$$|-〉=H|1〉=\frac {1}{\sqrt{2}}(|0〉+|1〉)$$

En efecto, los coeficientes descritos en $[B]$ se aproximan a $\frac{1}{\sqrt{2}}$ cuando se tiene un gran número de mediciones aleatorias consecutivas.

Hadamard y Método de Montecarlo

Sea $Ntest \in N$ tal que $Ntest\geqslant 10^{3}$ el número de mediciones aleatorias que realizaremos y sea $rnd \in ]0,1[$ el valor Real aleatorio que se genera en cada medición. Entonces con este criterio separamos los dos estados posibles. Nótese que todos los puntos están dentro del modelo, dado que cada punto aleatorio que se genera cae al interior una de las áreas definidas en el experimento:

$$ rdn = \begin{cases} \lt 1/2, & \text{ (i) } n_1=n_1+1 \\ \gt 1/2, & \text{ (ii) } n_2=n_2+1 \end{cases} $$
De modo que cada estimador del coeficiente $\hat\alpha_i^{2}$, se le asigna la proporción $n_i/Ntest$, i.e.

$$\hat\alpha_i^{2}\longrightarrow \frac{n_i}{Ntest}\text{, }\qquad \text{ donde } i=1,2$$

Este hecho, de apariencia trivial que se muestra en la animación gráfica que se realiza aplicando el método numérico expresado en la rutina de la función javascript "Distribucion_Aleatoria(Ntest)", - sobre un cuadrado de área $1$ -, dividido en la mitad.

A partir de esos resultados, se evalúa la proporción de $n_1$ y $n_2$ sobre el total de mediciones que arroja puntos sobre ese espacio. La distribución de los hits producirá una solución cada vez más aproximada de los coeficientes de [B] en la medida que el tamaño de las pruebas múltiples es de mayor magnitud, y consecuentemente cuyo error absoluto de la estimación irá decreciendo. (El Método de Montecarlo tiene un error absoluto de la estimación que decrece como $\frac {1}{\sqrt {Ntest}}$ en virtud del Teorema Central del Límite⁷⁴).

En efecto, el experimento se caracteriza por ser dicotómico y demostrará que el 50% de los puntos caen dentro de una se las subareas del modelo. Obviamente, cuantos más puntos se generen, menor será el error de la estimación.

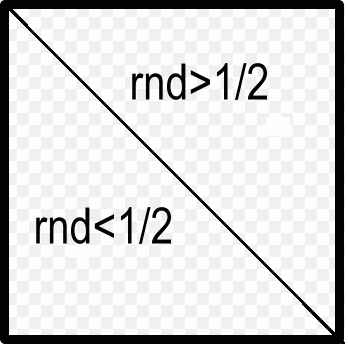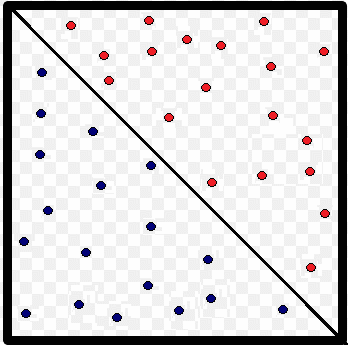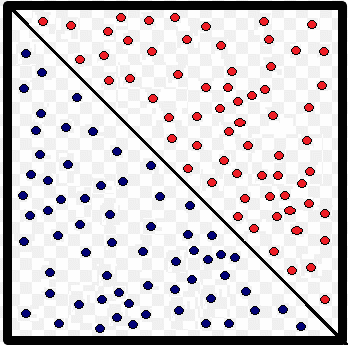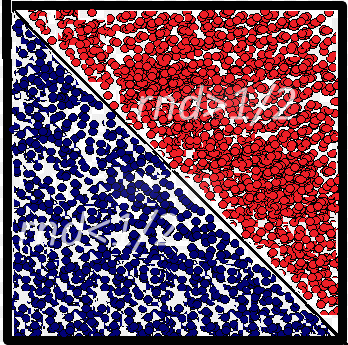
A continuación un simulador, que demuestra que cada vez que se selecciona una opción más grande de tamaño de la muestra $Ntest$, desde el ListBox. Es así que la resultante del experimento, va aproximando el error $\epsilon \longrightarrow 0$, permitiendo demostrar mediante el Método de Montecarlo que los vectores de la base de Hadamard son equiprobables.

Síntesis

Lo realizado con el Método Montecarlo para estimar $\hat\alpha_i$, en el límite cuando $nTest\longrightarrow\infty$, es asociar la probabilidad de un conjunto de $n_i$ valores aleatorios, - que llamamos $rnd$ a cada uno de ellos -, que hayan caído dentro del subespacio muestral $\Omega_i$, con $i=1,2$.

Donde asumimos⁸⁵ que $\Omega =\Omega _1 \cup \Omega_2\quad \land \quad\Omega_1 \cap \Omega_2=\emptyset$, para definir los tiros al azar $rnd$, los cuales caen en una de las dos áreas que dividen el cuadrado de lado $1$ y que van determinando el valor de los contadores $n_1$ y $n_2$.

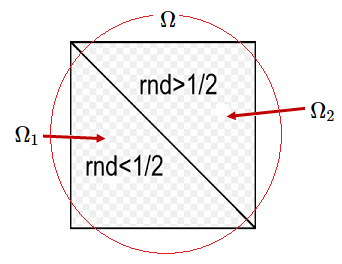$$rdn = \begin{cases} \lt 1/2, & \text{ (i) } n_1=n_1+1 \\ \gt 1/2, & \text{ (ii) } n_2=n_2+1 \end{cases} $$

Nótese que la cardinalidad del espacio muestral $\unicode{35}\Omega=Ntest$ y la probabilidad esperada se estima como $\hat\alpha_i^{2}=\frac{n_i}{Ntest}$, i.e. $\unicode{35}\Omega_1=n_1 \quad \land \quad\unicode{35}\Omega_2=n_2$. Obsérvese que todos los $rnd$ generados son puntos que caen dentro de $\Omega$.

Es decir, en este caso de la Amplitud de Probabilidad de la Puerta de Hadamard, simplifica la utilización del método porque ya está reducido el problema al cálculo del valor esperado o esperanza matemática del valor aleatorio, hacia al cual debe tender los estimadores $\hat\alpha_i^{2}\quad$, i.e. $\boldsymbol{(\frac{1}{\sqrt{2}})^2=\frac{1}{2}}$.

$$|+〉=H|0〉=\boldsymbol{\frac {1}{\sqrt{2}}} (|0〉+|1〉)$$
$$|-〉=H|1〉=\boldsymbol{\frac {1}{\sqrt{2}}} (|0〉-|1〉)$$

En síntesis, tal como se aprecia en el simulador, el experimento aleatorio del Método de Montecarlo demuestra que la magnitud de la repetición del número de los (independientes uno del otro) ensayos aleatorios del parámetro de entrada $Ntest$, aproxima en el límite el módulo al cuadrado de la Amplitud de Probabilidad de la puerta de Hadamard (Ver $[B]$), con un error cada vez más minúsculo.

$$nTest\longrightarrow \infty \quad \Rightarrow \quad \hat\alpha_i \longrightarrow \alpha_i=\frac{1}{2}\quad \Rightarrow \epsilon \longrightarrow 0$$

Observación Acerca del Método de Montecarlo

Para que la Teoría de la Medida opere sobre afirmaciones de probabilidades y valores esperados de ciertas variables aleatorias de un experimento, necesita que se cumplan algunos lineamientos iniciales: consistencia del enunciado, especificación del modelo para probar la hipótesis de la predicción, estimación de los parámetros elegidos, verificar la inferencia estadística, sumado ciertamente a otros preceptos según el contexto del problema a tratar.

El valor esperado es un concepto que requiere de algún tipo de conocimiento o intuición acerca de uno o más de los parámetros investigativos (Ver por ejemplo Naïve Bayes). Es decir, la operatividad del Método de Montecarlo funciona apropiadamente si están bien definidas las clases (sea intervalos, polígonos, u otros tipos de espacios en la partición). En otras palabras, aunque el número de ensayos aleatorios tienda a infinito, no estará garantizado que se logre la esperanza matemática o el "valor real" buscado. Se puede cubrir el espacio muestral $\Omega$ con los puntos aleatorios generados, sacar los estimadores por clase, obtener el error aleatorio, configurar una función de distribución, etc.. Pero sus resultados no serán un conjunto valido de solución.

Experimento con la Distribución Binomial

Este experimento de lanzar $nTest$ puntos o ensayos, distribuidos en $n_1 + n_2$, y definir la variable aleatoria como $\hat\alpha_i=\frac{n_i}{nTest}$, nos señala a través de la intuición y la experiencia que se debe tomar el $nTest$ lo más grande posible.

El experimento demuestra que las variabilidad aleatoria de los estimadores de las amplitudes de probabilidad $\hat\alpha_1$ y $\hat\alpha_2$ tienen el mismo valor esperado, i.e. su dispersión depende de $nTest$.

Desde el punto de vista de distribución estadística, los eventos tienen por un lado la probabilidad $p$ de caer dentro del espacio $\Omega_1$ y por otro lado la probabilidad $(1-p)$ de caer en el espacio $\Omega_2$. Entonces la probabilidad de que el evento ocurra exactamente $k$ veces - (en este experimento $k\geq 10^{3}$) -, viene dado por la distribución binomial:

$$p_k=\left(\begin{matrix}nTest\\\ k \end{matrix}\right)= p^{k}(1-p)^{nTest-k},\qquad \sum_{k=0}^{nTest} p_k=1$$