Propiedades Geométricas Cualitativas

Las propiedades de las figuras que se enuncian explícitamente en la geometría elemental son, en su mayor parte, propiedades métricas, es decir, propiedades que dependen de magnitudes o medidas. Tales son, por ejemplo, la igualdad de dos triángulos, la de dos ángulos, la propiedad de un cuadrilátero de ser cuadrado, etc.

Pero ciertas propiedades de las figuras son completamente independientes de magnitudes y medidas, y no se consideran por separado en geometría elemental.

Como idea consideremos el sólo el agua al interior de un vaso de agua que hemos localizado en la previa imagen de arriba, la cual se puede transformar en diferentes figuras, - en este caso en la forma de una plato bajo -, pero los puntos que conforman cada una de ellas son los mismos. Es decir, debe existir una función continua y biunívoca entre cada una de las distorsiones, que da lugar a una propiedad geométrica diferente a la elemental. (Ver Algebra de Lie $M_n(K)$ - Aplicaciones ~ Formalización)

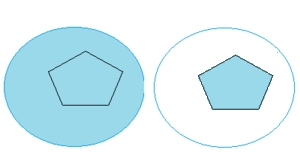
Otro ejemplo simple, pero no trivial: Consideremos la parte interior de un círculo, de una elipse, de un cuadrado y por otro lado consideremos, una corona circular o circunferencia. Todas estas figuras tienen, evidentemente, propiedades métricas diferentes. Sin embargo, la intuición nos señala que hay en las tres primeras algunas propiedades comunes, pero que la circunferencia no posee.

En efecto, las figuras tienen, por ejemplo, esta propiedad en común: cualquiera sea la línea poligonal simple cerrada situada en el interior de una de ellas, la superficie limitada por tal línea pertenece completamente al interior de la figura. Es claro que la corona circular no posee esta propiedad. Por tanto, se puede decir que hay ciertas propiedades cualitativas que el interior de un círculo, el de una elipse y el de un cuadrado tienen en común, pero que el interior de una circunferencia no posee.
 

Consideremos ahora una circunferencia en el plano. Esta divide el resto del plano en dos partes. Dos puntos de una misma parte pueden unirse siempre por medio de una línea poligonal plana sin que ésta corte a la circunferencia, mientras que toda línea poligonal plana que una dos puntos cualesquiera pertenecientes a cada una de las dos partes, respectivamente, corta a la circunferencia. Pero, se puede modificar convenientemente la forma métrica de la circunferencia sin alterar esta propiedad: si se remplaza la circunferencia por una elipse o una línea poligonal simple, cerrada, esta propiedad subsiste.

Nótese que el grafo de $11$ puntos que representa el logo de DocIRS, es un exponente de una geometría cualitativa (Ver Diseño y Construcción Gráfica de Logo DocIRS). Eso es lo que la representa la empresa, dado que su quehacer es unir puntos, a través de las más diversas relaciones tecnológicas y de gestión. Sin embargo, para la vista estética del logo,  la distribución de los $11$ puntos del grafo conexo (árbol), se construyeron geométricamente mediante una función basada en una circunferencia de radio $r$ con $8$ puntos de ángulos modulo $\frac{\pi}{4}$ y $2$ puntos externos a distancias $|r|$.

La Teoría de Grafos es una "geometría cualitativa" en la que se deja a un lado nociones cuantitativas como longitud, ángulo, área, volumen, etc. (propias de la geometría clásica) y se centra más bien en nociones cualitativas. En efecto, los grafos se expresan sólo sobre puntos (o nodos) y líneas.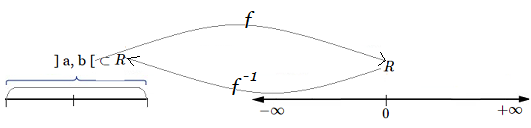

Otra rama de la matemática llamada Topología (Analysis Situs) enfoca el mismo concepto como, por ejemplo, si tiene agujeros o no, borde, o si se puede partir en componentes conexas, etc. Especialmente si existen funciones continuas y biunívocas entre espacios.

Aquí sería interesante mencionar las conjeturas relacionadas a conjuntos infinitos (Ver paradojas de la teoría de los conjuntos de Georg Cantor). En efecto, por ejemplo el  subconjunto de los Reales intervalo abierto $U=]-\frac{\pi}{2},\frac{\pi}{2}[$ es topológicamente equivalente al conjunto de los Reales, dado que existe al menos una función continua y biyectiva entre estos dos conjuntos. (Ver $y=tan(x)$ o $y=arctan(x)$) que demuestra que los une biunívocamente. Es decir, un subconjunto   tiene la misma cantidad de puntos que el conjunto que lo contiene.

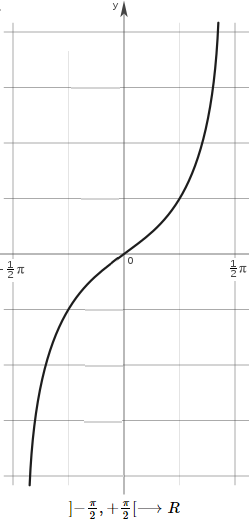
Esto, los convierte en espacios homeomorfos mediante $y=arctan(x)$, i.e. $\forall x\in U \text{ }\exists \text{ } \mathbf{f}\in \mathbb R$.

En efecto, la función:

$$\mathbf{f:}]-\frac{\pi}{2}, +\frac{\pi}{2}[\subset \mathbb {R}\quad \longrightarrow \quad ]-\infty,+\infty[=\mathbb{R}\quad \text{, donde } \mathbf{y=f(x)=tan(x)}$$
Nótese que

$$x \longrightarrow -\frac{\pi}{2}\quad \Rightarrow \mathbf{y}\longrightarrow -\infty \\ x=0 \quad \Rightarrow \mathbf{y=0} \\ x \longrightarrow +\frac{\pi}{2}\quad \Rightarrow \mathbf{y}\longrightarrow +\infty$$

El arcotangente es la función inversa de la tangente. Es decir, $\mathbf{y^{-1}=arctan(x)} \iff x=tan(y)$.

Se considera a Leonhard Euler el creador de la Teoría de Grafos (Ver Frank Harary, "Graph Theory", USA Addison-Wesley 1999 ) y pionero de la Topología al resolver el famoso problema de los puentes de Königsberg. A mediados del siglo XIX, siguieron otros problemas del mismo estilo. El más famoso es sin duda el problema de colorear un mapa con sólo cuatro colores (planteado por Francis Guthrie), el Camino de Hamilton, etc..