|
Ejemplo Simple Por Permutaciones
¿Cuál es la ruta óptima que pasa por cada
punto una vez?
José Enrique González
Cornejo
01 de mayo 2009
|
El artículo central del presente
ejemplo son:
i) Ruta Optima;
ii)
Simulación Por Tramos, iii)
Simulación Por Permutaciones.
El ejemplo está diseñado por partes, para facilitar
la posterior construcción del
algoritmo con N puntos. Se
ilustra sólo con 4 puntos, cómo determinar
la ruta óptima que pasa exactamente una vez
por cada punto y regresa al origen. Este ejemplo fue
desarrollado por el autor, debido a las numerosas
visitas e impresiones que ha tenido el artículo Ruta
Optima, desde su
publicación en mayo del 2009. |
- Parte I: Sin regresar al punto de partida u origen
Supongamos tenemos 4 clientes. Sea P={1,2,3,4} los puntos donde
se encuentra los clientes, cuya Matriz de Costo o Distancia,
d (i, j) asociada al grafo G, es simétrica.
|
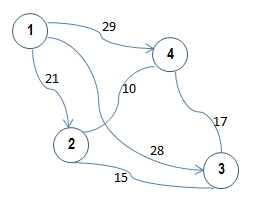
Grafo Completo G |
| |
1 |
2 |
3 |
4 |
| 1 |
0 |
|
|
|
| 2 |
21 |
0 |
|
|
| 3 |
28 |
15 |
0 |
|
| 4 |
29 |
10 |
17 |
0 |
Matriz de Costo, d(i,j)
Nótese que la diagonal es 0, dado que d(i,j)=0 cuando i=j.
d(i,j) = d(j,i). Es decir, costo de ida igual al de vuelta
|
Los 6 posible caminos tabulados por extensión los denotamos con letras.
Sea T={A,B,C,D,E,F}
los trayectos que parten desde el punto 1:
| A = |
{1, |
2, |
3, |
4} |
| B = |
{1, |
2, |
4, |
3} |
| C = |
{1, |
3, |
2, |
4} |
| D = |
{1, |
3, |
4, |
2} |
| E = |
{1, |
4, |
3, |
2} |
| F = |
{1, |
4, |
2, |
3} |
Nótese que el número de trayectos es (n-1)! , sin retorno a 1
donde n es el número de puntos
Asociando el costo d(i,j) a cada trayecto se tiene los costos por trayecto de
T:
| |
|
|
|
 |
| cA = |
21 |
15 |
17 |
53 |
| cB = |
21 |
10 |
17 |
48 |
| cC = |
28 |
15 |
10 |
53 |
| cD = |
28 |
17 |
10 |
55 |
| cE = |
29 |
10 |
15 |
54 |
| cF = |
29 |
17 |
15 |
61 |
Es decir, d(1,2)=21; d(2,4)=10; d(4,3)=17 =>
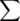 d(i,j) =
48 d(i,j) =
48
Ahora se busca en la columna Total el costo mínimo, para recorrer los 4
puntos partiendo del punto 1. El camino B presenta el costo mínimo de 48 unidades.
Por tanto, el algoritmo selecciona un punto de
partida, - en nuestro caso el punto 1-, y va armando todas las
trayectorias que recorran todos los puntos. Suma los costos
d(i,j) de cada tramo y finalmente determina la suma mínima.
Si la ruta óptima incorpora el retorno al
punto de partida, entonces existe una variación el el cálculo, dado
que debemos sumar los costos d(1,j)
| |
|
|
|
r1 |
 |
| cA = |
21 |
15 |
17 |
29 |
82 |
| cB = |
21 |
10 |
17 |
28 |
59 |
| cC = |
28 |
15 |
10 |
29 |
57 |
| cD = |
28 |
17 |
10 |
21 |
49 |
| cE = |
29 |
10 |
15 |
21 |
50 |
| cF = |
29 |
17 |
15 |
28 |
57 |
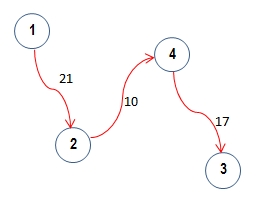
Nótese que con retorno al punto de partida
el número de combinaciones es n!
En efecto, al incorporar el retorno al punto de
partida el camino óptimo es D con un costo de 49 unidades.
Es decir, d(1,3)=28; d(3,4)=17; d(4,2)=10;d(2,1)=21 =>
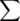 d(i,j)=49 d(i,j)=49 |

