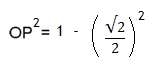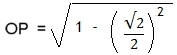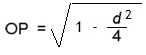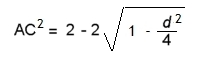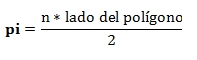Algoritmo de Arquímedes para el Cálculo de PI

Gracias a
Arquímedes
(Siracusa, Sicilia, 287 - 212 a.c.)

JEGC

Cálculo de PI
Algoritmo de Arquímedes

José Enrique González Cornejo
Noviembre 2015

Indice

Introducción

La constante pi, - denotada con la letra griega π, es la razón entre el perímetro de una circunferencia y su diámetro, definida en el plano.

El presente artículo es para mostrar el algoritmo de Arquímedes en el cálculo del valor de pi, comenzando por una simple función escrita en javascript. La función, - que hemos denominado Calculo_Pi() -, realiza la aproximación de la constante, según el procedimiento geométrico aplicado por matemático griego Arquímedes, que explicaremos a continuación.

El cálculo de aproximación del valor pi se ha realizado de diversas formas a lo largo de la historia de las matemáticas. Aquí nos limitaremos sólo al método de Arquímedes, no incursionaremos en Cálculo Infinitesimal e Integral, (limites, trigonometría, series, etc.) o en la llamada la matemática moderna. En realidad, en este potente procedimiento, Arquímedes ya muestra la génesis de las bases del Cálculo actual.

En Internet está lleno de descripciones, reconocimientos a Arquímedes, videos y de numerosos procedimientos, cuyo fin es calcular pi. Nos sumamos a los tributos, con un breve programa computacional sobre una pagina Web, para que el lector analice los códigos, los copie, los pegue en un editor y los ejecute con un navegador.(Explorer, Chrome, FF, Opera, Safari, etc.) Así mismo comprenda el desarrollo matemático del calculo utilizando sólo geometría euclidiana plana.

Animación Gráfica Concepto

Orden del Articulo

Empezamos presentando primero la función en javascript depurada del método; una tabla con iteraciones (nótese que se utiliza como límite ε =10^-m. Es decir, el parámetro m es el exponente negativo de 10 y se aplica como el margen de error); descripción breve del contexto euclidiano de Arquímedes; análisis geométrico inicial, a partir del cuadrado inscrito en la circunferencia, señalando el procedimiento de iteración que va duplicando los lados de cada polígono; el diagrama de flujo del algoritmo que transformaremos en la rutina computacional en javascript; una animación gráfica didáctica del concepto; y finalmente, se presentan los códigos de una pagina Web, con un botón que permite ejecutar el script. Nótese que en el encabezado del artículo, se localizó un índice que despliega un menú con los párrafos de la monografía.

Función Javascript y Estimaciones

function Calculo_Pi(m)
{
//Author: DocIRS-José Enrique González Cornejo
   var n=4
   var d=Math.pow(2,0.5)
   var pi=n*d/2
   var y=(-1)*m
   var epsilon=Math.pow(10,y)
    while (true)
    {
     var p1=pi
     n=2*n
     var auxiliar1=Math.pow(1-d*d/4,0.5)
     var d=Math.pow(2-2*auxiliar1,0.5)
     pi=n*d/2
     if (Math.abs(p1-pi)<epsilon){break}
    }
return pi
}

Función Calcula_Pi(9) en Javascript

Tabla con Iteraciones

La siguiente tabla muestra la aplicación de la función Calculo_Pi(m) , con m=1,2,...9. Donde el valor epsilon en cada fila toma el valor 10^-m. Se publican también en esta Tabla#1 los valores intermedios n, d, pi estimado y error, -o diferencia en valor absoluto del pi de la iteración anterior con el actual-. Se visualiza en los valores estimados, que a partir de ε^-9 el error es muy cercano a cero.

Epsilon 10^-m	N°Lados n	Longitud Lado Polinomio d	Estimación pi n*d/2	Error \|p1 - pi\|
1	16	0.3901806440322566	3.121445152258053	5.997769334e-2
2	64	0.0981353486548356	3.140331156954739	3.782666409e-3
3	128	0.049082457045824326	3.141277250932757	9.460939780e-4
4	512	0.012271769298312041	3.1415729403678827	5.913922374e-5
5	2048	0.0030679603725631203	3.141591421504635	3.696224674e-6
6	4096	0.0015339806375054086	3.141592345611077	9.241064416e-7
7	16384	0.00038349519451455667	3.1415926334632482	5.691824390e-8
8	65536	0.0000958737989905156	3.1415926453212153	9.486373909e-9
9	2097152	0.0000029960599457786747	3.1415965537048196	0.000000000e+0

Tabla#1. Estimaciones de pi, con ε=10^-m, con m=1,2,...9...n
Nótese que la constante π es un irracional y puede tener infinitos decimales.

Arquímedes y su Contexto

El algoritmo de la función desarrollada, está basado en siguiendo el enfoque geométrico que Arquímedes desarrolló alrededor de 300 años antes de Cristo, aplicando un método de geometría euclidiana para calcular este valor Irracional.

En efecto, Arquímedes buscó una forma de calcular la relación, - ya conocida en ese tiempo-, que existe entre el perímetro de una circunferencia y su diámetro, usando polígonos regulares inscritos o circunscritos.

El sorprendente resultado fue una estimación de la constante mucho más aproximada que todas las estimaciones anteriores. Valor que incluso se usa hasta hoy, en matemática, física y todas las ciencias que requieren este número. (En los siglos anteriores a Arquímedes, la aproximación era más tosca).

Nótese que aún no se conocía formalmente el conjunto de los números Reales, y lo más probable que Arquímedes lo quiso expresar como un Racional, lo mismo que raíz de 2.

Arquímedes comenzó a aproximar esta longitud en una circunferencia de un radio dado (asumamos 1), con un método muy utilizado para calcular áreas y perímetros desde hace miles de años, que es dividir y medir en pedacitos regulares y después sumar.

Por tanto, el problema de Arquímedes se reducía a calcular el perímetro de una circunferencia, porque que el diámetro está dado de acuerdo a la construcción elegida. El seleccionó una circunferencia de radio=1. Es decir, diámetro=2.

Desde esa construcción, Arquímedes fue inscribiendo polígonos regulares en dicha circunferencia y calculando su perímetro, llegando a tener cálculos de un polígono inscrito de 96 lados, partiendo desde el cuadrado. (Nótese que este mismo método se puede aplicar desde fuera de la circunferencia, armando una envolvente de polígonos regulares circunscritos).

Proceso Geométrico de Arquímedes

A partir del cuadrado, fue estimando el perímetro de la circunferencia (como si fuera el perímetro del polígono inscrito) y dividiéndolo por el diámetro. Es decir, en cada iteración, calculaba la longitud del lado y el número de lados del polígono, y por tanto, - multiplicando estas dos cifras-, el perímetro estimado, el cual lo dividía por el diámetro dado.

Figura 1

En la figura tenemos un círculo de radio 1, donde el cuadrado inscrito tiene lado √2, dado que en el triangulo rectángulo AOB se tiene:

AB² = AO² + OB²

=> AB² = 2

=> AB = √2 , Sea d = AB (Las iteraciones en algoritmo, se harán en función de d)

Ahora, consideremos la línea OC pasando por el punto P. Esta línea divide en la mitad el segmento AB, la que permite calcular el lado AC del siguiente polígono regular de 8 lados (primera iteración) y así sucesivamente se irá duplicando el numero de lados del polígono.

Por tanto,

AC² = AP² + CP², donde AP = d/2

CP = OC - OP

CP = 1 - OP, dado que OC=1

donde, OP² = OA² - AP²

Atención, si CP = 1 - OP → CP² = 1 - 2*OP + OP²y AP = d/2. Entonces, se calcula el lado AC, (Segmento rojo en la Figura 1)

AC² = AP² + CP², sustituyendo en función de d, se obtiene:

A partir del valor AC, que representa la longitud del lado del polígono regular, obtendremos el valor de

Así sucesivamente, se duplica el polígono regular inscrito en la circunferencia, se calcula la nueva longitud del lado en función de d y el número de lados n, de ese modo cada vez se obtiene una aproximación de pi más certera.

Diagrama de Flujo del Algoritmo

Códigos en Pagina Web

Los código HTML, con un comentario por cada instrucción de la función Calculo_Pi(), la cual está escrita en lenguaje Dom Javascript, está desarrollada para que el lector copie los códigos, los pegue en un editor Web y la ejecute con su navegador favorito.

<HTML>
<HEAD>
<TITLE>Calculo de PI - Arquímedes</TITLE>
<META NAME="Author" CONTENT="DocIRS: José Enrique González Cornejo">
</HEAD>
<BODY>

<div align="center">PI = <span id="sp_muestra_pi"></span> </div>
</BODY>
</HTML>
<script>
function Calculo_Pi()
{
///La función es calculada con el desarrollo geométrico de la figura 1
/// Sea el valor pi = Perímetro_circunferencia dividido por el diámetro_circunferencia,
//donde el diámetro es 2*r=2

var n=4 ///Numero de lados del polinomio inicial (Cuadrado de lado raíz de 2)

//Sea c valor inicial hipotenusa de triángulo rectángulo AOB de lado raíz de 2, diagonal.
//Es decir, c igual a raíz de 2, que es la longitud del lado del cuadrado inscrito.

var d=Math.pow(2,0.5)

/// aproximación del primer pi, asumiendo que el perímetro inicial de la circunferencia n*d //dividido por diámetro 2
///Donde 2 es el diámetro del la circunferencia

var pi=n*d/2

//// Error epsilon elegido suficientemente pequeño

var epsilon=Math.pow(10,-9)

/////////
////// Rutina que irá sucesivamente dividiendo el cuadrado inicial,
///// construyendo polígonos inscritos de más lados (duplicando).
///Hasta que la diferencia del valor absoluto estimado anterior menos el actual
/// Se menor que el espsilon arbitrariamente elegido.

while (true)
{
var p1=pi ///va asignando en la variable p1 el valor aproximado de pi, según la iteración
n=2*n //duplica el numero de lados del polígono
var auxiliar1=Math.pow(1-d*d/4,0.5) /////Calcula raiz cuadrada de OP
var d=Math.pow(2-2*auxiliar1,0.5) /// Saca el valor de AC
pi=n*d/2 // el perímetro del polígono dividido por el diámetro
if (Math.abs(p1-pi)<epsilon){break} ///Valor absoluto de la diferencia de pi anterior con el nuevo.
/////Hasta que esta diferencia es menor que epsilon
}
return pi /// Arroja el valor de pi aproximado con el error epsilon
}
document.getElementById("sp_muestra_pi").innerHTML=Calculo_Pi() //Carga resultado en el objeto span
</script>