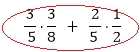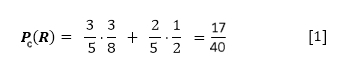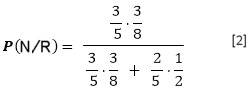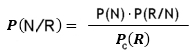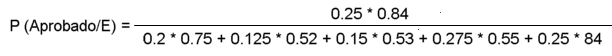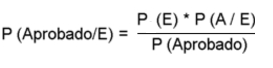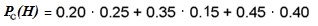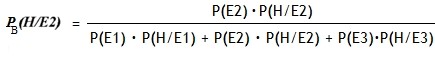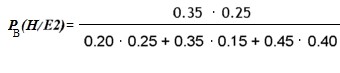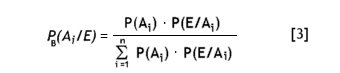|
|
|
|
José Enrique González Cornejo |
|||||||
| Resumen de la Regla
("Learning by Example") |
|||||||
|
Experimento
|
|||||||
|
Diagrama de árbol según el experimento |
|||||||
|
|||||||
|
Respuesta Expresión [2]  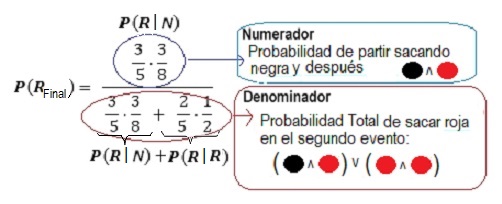
|
|||||||
|
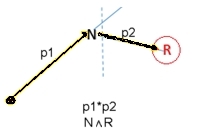
La notación de probabilidad condicional P(R|N) se lee como la probabilidad de que ocurra el evento R, dado que ya ocurrió el evento N. En muchos experimentos o situaciones reales, una información previa cambia el contexto de probabilidad. Es decir, mide esa probabilidad ajustada considerando que N ya sucedió. La notación de la expresión en el numerador de la fórmula de Bayes es P(N) $\cdot$ P(R|N) se lee como el producto de la probabilidad de sacar en el primer evento una bolita negra, transferirla al segundo buzón y posteriomente en el segundo evento, sacar una bolita roja (Probabilidad Condicional). En el diagrama de árbol es la rama superior: N $\longrightarrow$ R $$\underbrace{P(\text{N}) \cdot \ P(\text{R} \mid \text{N})}_{\text{Negra}\quad \land \quad \text{Negra dado Roja}}$$ La notación de la expresión en el denominador de la fórmula de Bayes es P(N)·P(R|N) + P(R)·P(R|R) se lee como la suma de los productos de las probabilidades de sacar en el primer evento una bolita negra y transferirla al segundo buzón y posteriomente en el segundo evento sacar una bolita roja o sacar en el primer evento una bolita roja y transferirla al segundo buzón, posteriomente en el segundo evento sacar una bolita roja. Esta suma es la Probabilidad Total restringido a sacar rojas en el segundo evento.
Descripción del Resultado
Se aplicó el Teorema de Bayes, para obtener la respuesta dada en la expresión [2]. En efecto, obsérvese el diagrama de árbol asociado y desarrollemos:
Ver detalle ejemplo en capítulo I |
Aplicación Generadora de Diagramas de Árbol
|
|
Siempre quise explicar el Teorema de Bayes de una forma sencilla,
siguiendo un poco las pautas del matemático Paul R. Halmos en su obra Teoría
Intuitiva de Conjuntos.
Una de las razones es que el Teorema de Bayes admite introducir una componente de subjetividad para determinados cálculos, especialmente cuando se debe recurrir al conocimiento de expertos. Es decir, cuando no se cuenta con ciertas evidencias estadísticas y recurrentes y se asumen criterios fundamentados a priori. Este tipo de estimaciones es más frecuente en la práctica de lo se enseña en la academia. En realidad, el Teorema de Bayes entrega una regla sencilla para calcular la probabilidad de un evento E, dado una serie de sucesos con sus probabilidades condicionales que lo anteceden. Sin embargo, la mayoría de los ingenieros, economistas o profesionales que alguna vez lo estudiaron, - que yo he encontrado en mi trabajo -, cuando han necesita aplicar el concepto, simplemente lo han olvidado casi por completo e incluso tienen un mal recuerdo del teorema. ¿Por qué será? Recuerdo el año 1972, en la Universidad Técnica Federico Santa María de Valparaíso, haberme inscrito en la asignatura Algebra Abstracta, - después de haber estudiado y aprobado ramos como Lógica y Conjuntos, Algebras Vectoriales y Lineales, Cálculos, Probabilidades y Estadísticas y tres asignaturas de Física-, para encontrarme con que la bibliografía de base de este ramo Algebra Abstracta, era un libro llamado por todos los conocedores, como “el Halmos” a secas. Cuando comencé a hojearlo, grande fue mi sorpresa. Casi no había nomenclatura en sus textos, se describían los conceptos con ejemplos simples, sin expresiones matemáticas y creo, que todos aquellos jóvenes que deseábamos ser científicos, quedamos bastante descolocados. Incluso algunos preguntaron si el curso era de literatura. (Estábamos mal acostumbrados y con una concepción desviada de lo que realmente es la Matemática) Al menos, desacomodados en muchos aspectos, dado que habíamos cursado todas esas materias en forma aislada e inconexa, siempre basado en un enjambre de notación, nomenclatura matemática, demostraciones por el absurdo etc., que consecutivamente eran evaluadas en pruebas, por los docentes. Creo que cada uno de nosotros, - en sus largas y nocturnas horas de estudio y repetición de ejercicios, habíamos aprendido a sobrevivir y lograr, - de alguna forma-, pasar aquellos presionados certámenes. Me gustaría preguntarle a cada uno de estos destacados profesionales de hoy y jóvenes de ayer, ¿Cuánto le sirvieron los ejercicios del Schaum para preparar sus pruebas?. Es posible que mis compañeros Sansanos, nieguen haber preparado sus pruebas con estas útiles ediciones de la Mc Grau-Hill. (Utilizada por millones de estudiantes en el mundo). Luego, mis preguntas son:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Bueno, el presente artículo intenta enseñar el Teorema de Bayes basado centralmente en diagramas de árbol, sin asustarnos por la expresión de sus fórmulas, conceptos y notación, que son impresionantemente complejas cuando la vemos por primera vez. Aún más, sin tener aun mucha comprensión de cuál es su utilidad y de verse obligados a aprender desmenuzando nomenclaturas complejas. Seré uno más de los que intentan mejorar la reputación de Thomas Bayes ayudado por el enfoque intuitivo de Paul Halmos, de modo que partiré con el simple y frecuente ejemplo de dos buzones con bolitas de colores y su correspondiente diagrama de árbol, para explicar haciendo un experimento de probabilidades condicionales e ir introduciendo paulatinamente ciertos conceptos formales. Después ingresar del mismo modo al cálculo de
Bayes, con varios ejemplos y un segmento de una aplicación computacional
DocIRS (con javascript), para generar árboles mediante ingreso de parámetros (Ver
Aplicación Generadora de Arboles).
Aprenderemos dibujando el diagrama de
árbol. Recuerden el enunciado de un problema siempre debe tener los datos de base
explícitos o implícitos.
Finalizaremos con una conclusión basada en la experiencia de la empresa DocIRS en tratamiento estadístico de datos y un anexo con pautas para el lector.
I. Concepto a través de dos Buzones Experimento 1 Se tienen dos buzones. El Buzón 1 con 3 bolitas negras y 2 rojas. El Buzón 2, con 4 negras y 3 rojas.
El experimento aleatorio que utilizaremos, consiste en sacar una bolita del primer buzón e introducirla en el segundo, para después extraer una bolita de este último buzón y ahí preguntar probabilidades de ocurrencia. El hecho de sacar una bolita lo llamaremos evento, cuya probabilidad es siempre diferente de cero. (El experimento tiene como condición, siempre sacar una bolita)
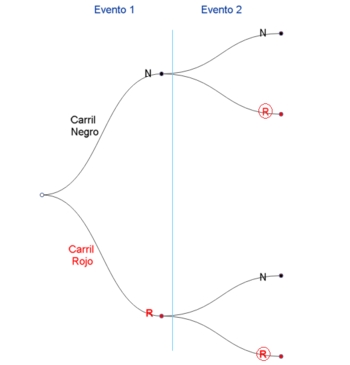
Pregunta: ¿Cuál es la probabilidad que sea roja? Para responder esta pregunta, se construye un diagrama en árbol, donde se definen dos carriles, y se asocia la probabilidad cada a cada rama. Nótese que Cada carril cuenta con dos ramas. (Utilizar Aplicación Generadora de Arboles con parámetros (2,2,0) para dibujarlo).
En el diagrama de árbol a continuación, asociamos las probabilidades a cada rama.
Primero se definen los eventos o sucesos con una notación clara:
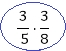
De ahí, utilizaremos la notación convencional, sobre
el segundo evento condicionado:
Después marcamos con un circulo rojo cada uno de los rojos posibles de sacar del Buzón 2. A partir del diagrama, calculamos la probabilidad de sacar una bolita roja del Buzón 2, dado el experimento en cuestión. Respondiendo la pregunta formulada: ¿Cuál es la probabilidad que sea roja?
(Nótese que esto significa que primero calcularemos la Probabilidad Total del sacar una bolita roja) La regla de ir calculando la probabilidad total de un experimento condicionado, basado en el diagrama de árbol es simple y ordenado. Cuando vamos por un carril (ramas consecutivas), se van multiplicando las probabilidades asociadas a las ramas. (conectiva booleana conjunción y).
Enseguida en el diagrama , nos movemos por el Carril Rojo y usamos la regla de la suma. Es decir, cuando bifurcan los carriles, entonces se debe sumar las probabilidades (conectiva booleana v, disyunción o) . De ese modo llegamos al suceso bolita Roja, usando regla de la multiplicación y la regla de la suma.
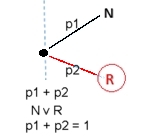
Nótese que la suma de las probabilidades de las ramas bifurcadas siempre debe sumar 1. Ahora, veamos qué se preguntaría el reverendo Thomas Bayes, autor del Teorema que analizaremos más adelante: ¿Cuál es la probabilidad de sacar una bolita
roja del segundo buzón, dado que la primera bolita fue negra? Llamemos PB(N/R) a esta probabilidad formulada por Bayes, para tener una notación coherente.
Es decir, tomamos la probabilidad de sacar una bolita roja, cuando partimos por el carril de las negras y lo dividimos por la probabilidad total de sacar una roja calculada en [1] y ahí tenemos una aplicación concreta del Teorema de Bayes. Observamos que el Evento2 está condicionado por el Evento1, por
eso son eventos llamados mutuamente excluyentes (o independientes). Es decir, para que
ocurra el segundo evento debe ocurrir el primero. Otra propiedad de
estos eventos, es que su probabilidad siempre es diferente de cero. • p(A
Entonces, el proceso estocástico se dará sobre los buzones 1 y 2, los cuales están cargados inicialmente con bolitas negras y rojas. Al poner en movimiento el experimento, observamos que cada uno de los eventos que lo constituyen, son sucesos probabilísticas y parte del espacio muestral (número total de posibilidades del experimento). Por tanto, la expresión con notación formal del calculo de la probabilidad en [1] es: Pc(R) = P(N)·P(R/N)+P(R)·P(R/R) Y la expresión con notación formal, calculada en [2] de acuerdo al Teorema de Bayes es:
Es decir, PB(N/R) en el marco del Experimento1, responde la pregunta ¿Cuál es la probabilidad de sacar una bolita roja del segundo buzón, dado que la primera bolita fue negra? II. Experimento Dado el Árbol y Cantidades Experimento 2
Realicemos un experimento al revés, donde está dado un diagrama de árbol con cinco fuentes de entregables, los cuales - en un segundo evento-, pueden ser rechazados o aprobados. Los valores de cada carril y rama son absolutos y nos preguntan: ¿Cuál es la probabilidad de que un entregable Aprobado provenga de D?. Transcribamos el árbol en tablas para determinar sus distribuciones probabilísticas. Al tener las cantidades de entregables A, B, C , D y E , con sus respectivas distribuciones en el segundo evento de Rechazados o Aprobados, entonces podemos asumir y asignar sus probabilidades. En efecto, la suma de los entregables es el espacio muestral del primer evento, los cuales suman 200 entregables:
E1: Distribución Cantidades por Carriles de Entregables
E1: Distribución de Probabilidades por Carril de Entregables
A continuación la distribución por ramas del segundo evento E2:
E2: Distribución de Rechazo o Aprobaciones por Carril
Por tanto la Probabilidad Total de ser un Entregable Aprobado es: $$ P(Aprobado)=0.2\times 0.75 + 0.125 \times 0.53 + 0.15\times 0.53 + 0.275 \times 0.55 + 0.75 \times 0.84 $$ y la probabilidad de que un entregable Aprobado que proviene de D, la obtenemos aplicando Bayes. Por tanto, siguiendo el carril E hasta Aprobado y diviendo ese valor por la Probabilidad Total de Los Aprobados:
Formalmente con la notación que estamos usando, la expresión queda así:
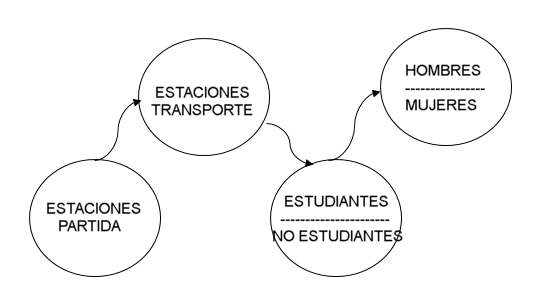
III. Asociando Datos Estadísticos A continuación ilustraremos como se asocia la frecuencia relativa, capturada como dato, a la la probabilidad del evento. En efecto, el uso práctico en el transporte, medicina, finanzas, usabilidad de determinadas navegaciones o rutinas de los usuarios en un sistema, o en todas las actividades y disciplinas donde se recaban datos en forma sistemática y bien clasificada, se utiliza como probabilidad la proporción del espacio muestral que ocupa. Estas observaciones, pueden ir creciendo en el tiempo. Es decir, la proporcionalidad de lo coeficientes y del tamaño del espacio muestral son dinámicos. En efecto, se asume que cuando las repeticiones son grandes y su número de observaciones crece en forma indefinida, entonces la frecuencia relativa converge hacia la probabilidad del evento, y se considera que las frecuencias relativas tienden a estabilizarse. La noción de frecuencia o de "a posteriori" es entonces de tipo empírico. Es necesario comprender que cuando la escala en ordenes de magnitud aumenta, seguramente variables discretas hay que intentar tratarlas como continuas e incorporar la estadística y modelos estadísticos bayesianos computacionalmente. En un sector de la ciudad, se contabilizaron 220.000 pasajeros que viajan en un período determinado, - entre las 12:00 y las 13:00 horas -, las cifras señalan que el 20% de esta población se transporta en la línea E1, un 35% se moviliza en la línea E2 y el restante en otras líneas (Llamemos E3).
Distribución - Evento1
La estadística muestra además que el 25% que ocupa la línea E1 son hombres, el 15% de los hombres la línea E2 y el 60% de las mujeres viaja en las otras líneas de transporte. Las distribuciones discretas de probabilidad se muestran, es las siguientes tablas a continuación:
Distribución Género por Líneas
¿Cuál es la probabilidad que un hombre haya utilizado la línea de transporte E2? 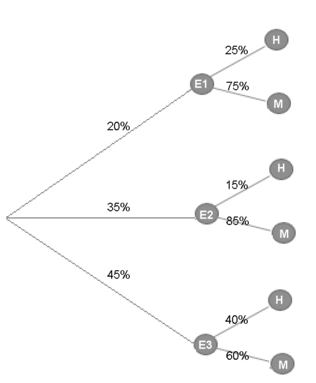 Diagrama 5 Es claro que se definen tres carriles en el Diagrama 5 de árbol, E1, E2 y E3. Donde cada uno de ellos cuenta con dos ramas binarias de género. Por tanto los eventos son: Pasajeros que pueden utilizar una de las tres líneas y desde ahí, el evento que el Pasajero pueda ser hombre. La Probabilidad Total de ser Hombre se calcula como: Pc(H) = P(E1) · P(H/E1) + P(E2) · P(H/E2) + P(E3)·P(H/E3) Es decir, en términos numéricos:
Aplicando el Teorema de Bayes:
IV. Formalización Matemática del Teorema de Bayes Sea E un evento de un espacio muestral S, y sean A1,A2,A3,...,An , eventos disjuntos, cuya unión es S. (Ver concepto de Partición en Conjuntos) Entonces para i = 1,2,3,....n, se tiene la siguiente fórmula:
Se considera que los eventos A = {A1,A2,A3,...,An} son causas posibles del evento E, de ahí que el Teorema de Bayes nos permite estimar la probabilidad de que un elemento particular de A ocurra siempre que el suceso E haya ocurrido. Nótese que una sucesión de observaciones A1,A2,A3,...,An se denomina Proceso Estocástico, cuando los valores de los Ai no son predecibles exactamente, pero si es posible tener sus probabilidades y responden a una relación de orden (generalmente en el tiempo). La importancia que tiene para empresas como DocIRS, donde uno de sus focos es el tratamiento documental de datos, análisis estadístico de contenidos, desarrollo y gestión de plataformas tecnológicas, para el control y seguimiento de proyectos y contratos, es entender que el Teorema de Bayes nos ayuda y nos induce a abrir conocimiento permanentemente, mejorar los algoritmos y la gestión de calidad. La experiencia directa y sorprendente en DocIRS e inimaginable para cualquier pedagogo de la matemática, nos demuestra que un joven programador de computadoras, puede ir haciendo y desarrollando complejos algoritmos, sin tener el más mínimo conocimiento formal, ni teórico de la matemática. Tengo evidencias fehacientes de programadores, que en varias ocasiones han construido complicadas funciones en un lenguaje de alta programación-, respondiendo a un requerimiento determinado de un sistema. En efecto, al analizar los códigos de lo desarrollado, siempre encuentro relaciones complejas y múltiples, recurrencia, condicionales anidados con lógica de Boole, aplicación de series, espacios de probabilidades y clases de intervalos. Todas la rutinas las han construido intuitivamente, sin saber siquiera que existen esos conceptos, teoremas, propiedades y definiciones. Ni siquiera conocen su notación matemática y menos Teoría de la Medida. El logro es sólo por su oficio con el computador, en su lenguaje de programación y manejo que tienen sobre Internet. Por esa razón, dada una exigencia en una de nuestras plataformas, desarrollé una simple rutina a modo de ejemplo, donde apliqué el Teorema de Bayes, - sin mencionar el teorema, ni nada por el estilo -, solo utilizando un diagrama de árbol para la estimación de los resultados. La expliqué y traspasé al equipo de desarrollo asignándoles una serie de tareas análogas, pero más complejas. La experiencia me demostró una vez más, que es posible transmitir un conocimiento en forma "mecánica" o por recetas de cocina, como dirían los académicos. En efecto, una acertada aplicación del Teorema de Bayes nos fue señalando cómo debemos ir adaptando nuestros procesos, en función de las probabilidades, estimadas desde los datos almacenados en las bases de datos, requerimientos y accesos de usuarios, incidentes, fallas, reclamos, funcionamiento de nuestro networking, seguridad de la información, evolución del negocio del cliente, elementos que se están generando permanentemente. La estadística bayesiana de las transacciones en nuestras plataformas, las iniciamos con un conjunto de supuestos, que nos han permitido ir ajustándolos y mejorándolos en función de la evidencia empírica que recolectamos diariamente. Colección de datos que permiten estar creando posibles escenarios, probando y analizando, a fin de determinar resultados y su posible variabilidad, con eventos independientes, o dependientes, variables aleatorias, distribuciones de probabilidad, regresión lineales y proyecciones futuras.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Un problema para el lector Experimento 3 Continuemos diseñando un experimento que es una variante más compleja del experimento anterior, pero con magnitudes mayores, a fin de ir comprendiendo que la aplicación del Teorema de Bayes, - (que formalizaremos matemáticamente al final del articulo)-, requiere necesariamente la utilización del computador. Aún más, principalmente la combinatoria de muchos eventos exige el tratamiento computacional. Así mismo la graficación del correspondiente diagrama de árbol. Supóngase en forma limitada un problema de probabilidades de transporte público. Haremos abstracción de estaciones del año, días, horarios -, así mismo, inventaremos las distribuciones probabilísticas de datos. En efecto, trabajaremos con cifras de pasajeros que van utilizar la Línea 1 del Metro de Santiago de Chile, ingresando en la vecindad del barrio Estación Central. Nótese que sabemos que, - para cualquier empresa de transporte metropolitano-, contar los ingresos en las estaciones, son datos capturables mediante la tarjeta BIP (o torniquetes). No obstante, también sabemos que la estimación de las afluencias de salida, se emplean otras técnicas estadísticas para obtener mediciones. La variables género son aun más difíciles de medir, sólo las introduje para hacer más complicado el experimento. Los pasajeros que analizaremos ficticiamente, realizan sus ingresos por una de las
tres siguiente estaciones: Universidad de Santiago (E7); Estación
Central (E8) o Unión Latinoamericana (E9). La Línea 1 del Metro de
Santiago de Chile tiene 27 estaciones. Es decir, no consideraremos
las otras líneas existentes. Esto implica que se bajarán en una estación del metro de la Línea 1, diferente a donde se subieron. (No consideramos transbordos a las otras líneas existentes de Metro de Santiago). Los pasajeros que analizaremos pueden ser estudiantes (ES) o no
estudiantes (NE), de género Femenino o Masculino. Ahora asignaremos probabilidades en porcentajes estadísticos ficticios. La tabla con la probabilidad de salida de las 27 estaciones se hizo con una distribución aleatoria (Ver Algoritmo en Acción ~ Herramienta de Distribución Aleatoria de Suma 1), a fin de seguir aproximándonos al Teorema de Bayes de una más compleja, pero siempre heurística.
Distribución Ingresos
Distribución Estudiantes
Distribución Género por Líneas
Distribución Salidas
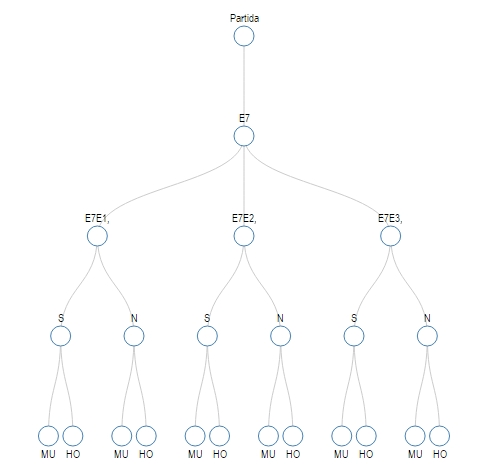
El numero de combinaciones son 3 · 26 · 2 · 2 = 312, dado que se pueden elegir 3 carriles; después se pueden elegir 26 estaciones diferentes (una de las 27 fue ocupada por el carril inicial); dos posibilidades de ser estudiante o no; y finalmente 2 posibilidades (hombre o mujer)
A fin de no tener que mostrar por extensión cada uno de los senderos, hemos agregado las estaciones en un conjunto E, de ese modo la rutina en javascript sólo ilustrará con 12 carriles las combinaciones, asumiendo que cada sendero se configura con un elemento del conjunto E. Por ejemplo: E7E11-ES-HO, que significa que salió de la estación E7, se bajó en E11 que era un estudiante hombre.
Combinatoria Resultado del javascript
Javascript que genera combinaciones
Pautas Javascript para el Diagrama de Arbol (ver Collapsible Tree - Ocks)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

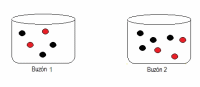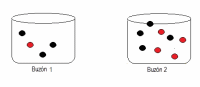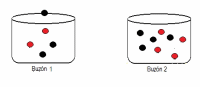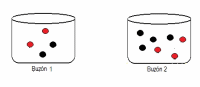


 Ver Video
Ver Video