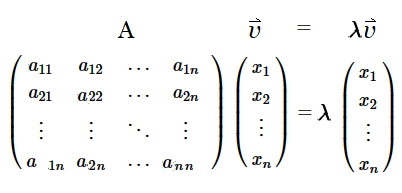|
+ Cálculo Autovectores |
Deducción Matemática
José Enrique González Cornejo
v.9.1/Abril 2021
Capítulo extraído del Documento de Base:
Matrices Cuánticas de Pauli ~ Base de un Algebra de Lie

 Vectores Propios $\longrightarrow$ Matrices de Pauli · Introducción - Deducción $\unicode{123}\large {\sigma_x,\sigma_y,\sigma_z}\unicode{125}$ 177
Se mostrará la deducción de los tres operadores lineales, a partir de $\sigma_z$, operador que gira en torno al eje de la $z$ del plano euclidiano de 3 dimensiones (representación sobre la superficie de la esfera de Bloch19), espacio donde, - en el presente artículo-, se ilustran las definiciones de las tres puertas de Pauli $\sigma_x=X$, $\sigma_y= Y$, $\sigma_z=Z$. 175
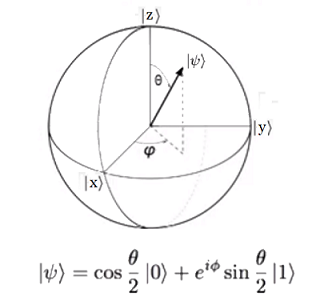 Espín:Matrices de Pauli Nótese que se actuará linealmente sobre los operadores {$X,Y$} como Estados en Superposición de los autovectores de base utilizados para configurar $\sigma_z= Z$.
Comenzaremos desde el sping del electrón, donde se tiene un estado hacia arriba (↑~$|u〉$) y un estado de la rotación hacia abajo (↓~$|d〉$). Equivalentemente se utiliza esta notación de Dirac1 como: $|0〉$ y $|1〉$.

Los operadores de Pauli se utilizan en física para describir el spin de las partículas, que es una propiedad intrínseca de las partículas elementales. El spin se comporta como un vector en un espacio tridimensional y los operadores de Pauli nos permiten describir matemáticamente sus componentes en cada una de las tres direcciones.
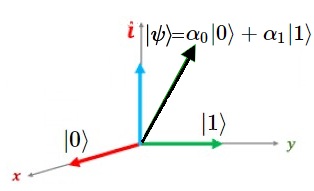 Dirac: Representación de Estados A fin de deducir el operador, se aplican los principios básicos de la mecánica cuántica. Es decir,
ii) Los autovectores de $\sigma_z$ son {$|u〉=+1,|d〉=-1$} 170; iii) Los vectores $|u〉$ y $|d〉$ son ortogonales, i.e. producto interno $〈u|d〉=0$2.
Matrices de Pauli~Esfera de Bloch19
· Eigenvectores o Vectores Propios
· ¿ De dónde aparece la constante normalizada $\large{\frac{1}{\sqrt{2}}}$ ? Sabemos del cálculo de autovectores que $A\vec{v}=\lambda\vec{v}$, siendo $A_{n \times n}$ una matriz cuadrada no nula ($A \ne \vec{0}$), y $\vec{v}_{n\times 1}$ es un autovector de orden $n \times 1$, con $\lambda \in \mathbb{C}\quad(\lor \quad \lambda \in \mathbb {R})$ es un escalar. Luego, resolviendo la ecuación matricial: $$ \begin{pmatrix} 0 & -i\\ i & 0\\ \end{pmatrix} \begin{pmatrix} x\\ y\\ \end{pmatrix} = (+1) \begin{pmatrix} x\\ y\\ \end{pmatrix} $$ Se puede determinar que una solución es el autovector columna $\vec{v_1}$ con autovalor $\lambda_1=+1$: $$ \begin{pmatrix} x \\ y \\ \end{pmatrix}= (+1)\underbrace{\begin{pmatrix} -i \\ 1 \\ \end{pmatrix}}_{\vec{v_1}} $$ En efecto, multiplicando la matriz $\sigma_y$ por el vector $\vec{v_1}$, con el autovalor asociado $\lambda=+1$ se obtiene $\vec{v_1}$: $$ \begin{pmatrix} 0 & -i\\ i & 0\\ \end{pmatrix} \underbrace{ \begin{pmatrix} -i \\ 1 \\ \end{pmatrix}}_{\vec{v_1}}= \begin{pmatrix} 0·(-i)+(-i)·1 \\ i·(-i)+0·1 \end{pmatrix}=\underbrace{\begin{pmatrix} -i \\ 1 \\ \end{pmatrix}}_{\vec{v_1}} $$ Ahora, la norma o módulo del eigenvector $\vec{v_1}$ es 176: $$ \begin{Vmatrix} -i \\ 1\end{Vmatrix} =\sqrt{|-i|^2+|1|^2}=\sqrt{2} $$ De ahí que, la normalización constante es $\large{\frac{1}{\sqrt{2}}}$ 
Así mismo en este artículo anexo, se esboza una demostración algebraica, a partir de las propiedades de la matrices de Pauli, operando matricialmente, generando ecuaciones y despejando para demostrar su conformación.
· Iniciando Deducción con la Matriz $\large {\sigma_z=Z}$ $$ \sigma_z = \begin{cases} |u〉=|↑〉+1 & \text{ (up)} \\ |d〉=|↓〉-1 & \text{ (down)} \end{cases} $$ 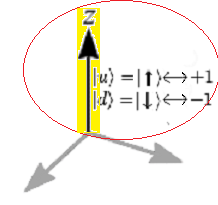
Los autovectores o eigenvectores de {$|u〉, |d〉$}, que al transformarlos en su medición por el operador $\sigma_z$, dan lugar a los escalares {$+1,-1$} respectivamente.
Vectorialmente se representan como vectores columnas de un espacio bidimensional: $$ |u〉=\begin{pmatrix} 1 \\ 0 \\ \end{pmatrix}\\ \land \\|d〉=\begin{pmatrix} 0 \\ 1 \\ \end{pmatrix} $$
Nótese que todos los posibles resultados de las mediciones son operadores del autovalor que representan un observable.
Además, estos dos vectores son ortogonales, i.e. el producto interno entre ellos es igual a cero:
Aplicando $[Eqs_z]$, considérese matricialmente entonces, - en este espacio vectorial bidimensional -, las siguientes dos ecuaciones:
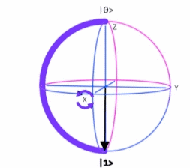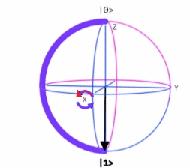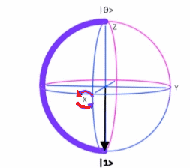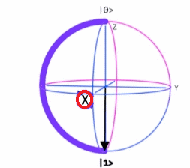
Se ha deducido la matriz unitaria $\sigma_z$ de Teoría Cuántica, que se denomina también Puerta Cuántica de Pauli $Z$. 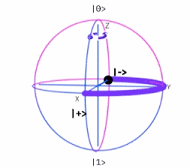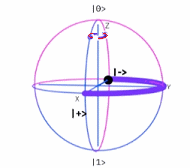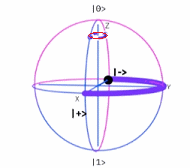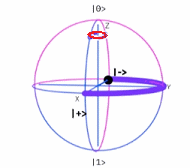 Operador $\sigma_z$~Esfera de Bloch Luego, con el mismo procedimiento y principios con que se dedujo este operador lineal $\sigma_z=Z$, se infieren las otras dos matrices de Pauli $\sigma_x=X \quad y \quad \sigma_y=Y$ 171 como combinación lineal de los vectores de base {$|u〉,|d〉$}. · Deducción Matriz $\large {\sigma_x=X}$
Denotemos dos vectores {$|r〉,|\ell〉$} como $(\rightarrow \text{ right})$ y $(\leftarrow \text{ left})$, para deducir el operador $\sigma_x$.
Desde ahí, se demostrará que:
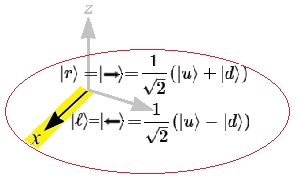 $$|r〉=\frac{1}{\sqrt{2}}(|u〉 + |d〉)\\ \land \\ |\ell〉=\frac{1}{\sqrt{2}}(|u〉 - |d〉)$$ Luego, se tienen los siguientes vectores columnas: $$ |r〉=\begin{pmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \\ \end{pmatrix} \\ \land \\ |\ell〉=\begin{pmatrix} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \\ \end{pmatrix} $$ Obsérvese que los vectores {$|r〉,|\ell〉$} son una superposición (equiprobable) de los vectores de base {$|u〉, |d〉$}, que se obtiene al realizar la rotación en torno al eje $x$. Aplicando $[Eqs_x]$, considérese matricialmente entonces las siguientes dos ecuaciones: $$ \begin{pmatrix} (\sigma_x)_{11} & (\sigma_x)_{12} \\ (\sigma_x)_{21} & (\sigma_x)_{22} \\ \end{pmatrix}· \underbrace{ \begin{pmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \\ \end{pmatrix}}_{|r〉}= \underbrace{ \begin{pmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \\ \end{pmatrix}}_{|r〉} \qquad [Eq_{x1}] $$ $$ \begin{pmatrix} (\sigma_x)_{11} & (\sigma_x)_{12} \\ (\sigma_x)_{21} & (\sigma_x)_{22} \\ \end{pmatrix}· \underbrace{ \begin{pmatrix} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \\ \end{pmatrix}}_{|l〉}= -\underbrace{ \begin{pmatrix} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \\ \end{pmatrix} }_{|l〉} \qquad [Eq_{x2}] $$ Multiplicando matricialmente $[Eq_{x1}]$ y $[Eq_{x2}]$ respectivamente, se obtiene: $$ (\sigma_x)_{11}=0 \text{ , }(\sigma_x)_{21}=1\\ \land \\ (\sigma_x)_{12}=1 \text{ , }(\sigma_x)_{22}=0 $$ Se ha deducido la matriz unitaria $\sigma_x$ de Teoría Cuántica, que se denomina también Puerta Cuántica de Pauli $X$. Matricialmente se expresa como:
 Operador $\sigma_x$~Esfera de Bloch · Deducción Matriz $\large {\sigma_y=Y}$ Denotemos dos vectores {$|i〉,|o〉$} como $in$ y $out$, para deducir el operador $\sigma_y$. $\sigma_y(|i〉)=+1|i〉=|i〉$ y $\sigma_y(|o〉)=-1|o〉=-|o〉$, i.e.
Es decir, se demostrará que
 $$|i〉=\frac{1}{\sqrt{2}}(|u〉 + i|d〉)\\ \land \\ |o〉=\frac{1}{\sqrt{2}}(|u〉 - i|d〉)$$ Obsérvese que los vectores {$|i〉,|o〉$} son una superposición de los vectores de base {$|u〉, |d〉$}, que se obtiene al realizar la rotación de $\pi$ radianes en torno al eje $y$. (Vectores que se asumen equiprobables) Luego, se tienen los vectores columnas, $$ |i〉=\begin{pmatrix} \frac{1}{\sqrt{2}} \\ \frac{i}{\sqrt{2}} \\ \end{pmatrix}\\ \land \\|o〉=\begin{pmatrix} \frac{1}{\sqrt{2}} \\ -\frac{i}{\sqrt{2}} \\ \end{pmatrix} $$ Aplicando $[Eqs_y]$, considérese matricialmente entonces las siguientes dos ecuaciones: $$ \begin{pmatrix} (\sigma_y)_{11} & (\sigma_y)_{12} \\ (\sigma_y)_{21} & (\sigma_y)_{22} \\ \end{pmatrix}· \underbrace{ \begin{pmatrix} \frac{1}{\sqrt{2}} \\ \frac{i}{\sqrt{2}} \\ \end{pmatrix}}_{|i〉}= \underbrace{ \begin{pmatrix} \frac{1}{\sqrt{2}} \\ \frac{i}{\sqrt{2}} \\ \end{pmatrix}}_{|i〉} \qquad [Eq_{y1}] $$ $$ \begin{pmatrix} (\sigma_y)_{11} & (\sigma_y)_{12} \\ (\sigma_y)_{21} & (\sigma_y)_{22} \\ \end{pmatrix}· \underbrace{ \begin{pmatrix} \frac{1}{\sqrt{2}} \\ -\frac{i}{\sqrt{2}} \\ \end{pmatrix}}_{|o〉}= -\underbrace{ \begin{pmatrix} \frac{1}{\sqrt{2}} \\ -\frac{i}{\sqrt{2}} \\ \end{pmatrix} }_{|o〉} \qquad [Eq_{y2}] $$ Multiplicando matricialmente $[Eq_{y1}]$ y $[Eq_{y2}]$ respectivamente, se obtiene: $$ (\sigma_y)_{11}=0 \text{ , }(\sigma_x)_{21}=i\\ \land \\ (\sigma_x)_{12}=-i \text{ , }(\sigma_x)_{22}=0 $$
Se ha deducido la matriz unitaria $\sigma_y$ de Teoría Cuántica, que se denomina también Puerta Cuántica de Pauli $Y$. Matricialmente se expresa como:
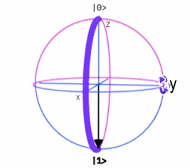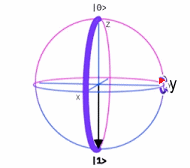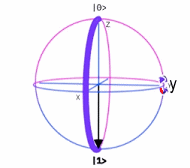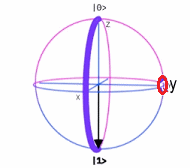 Operador $\sigma_y$~Esfera de Bloch Por tanto, tenemos las tres Matrices de Pauli en el espacio bidimensional: $$ \sigma_x= \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix} \qquad \sigma_y= \begin{pmatrix} 0 & -i \\ i & 0 \\ \end{pmatrix} \qquad \sigma_z= \begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix} $$ · Deducción Algebraica ~ Desde las Propiedades
Estas tres matrices de Pauli son representaciones matriciales de su operador unitario, que cumplen con la condición de que la determinante de su matriz es diferente de $0$ (toma el valor $\pm 1$), su traza $Tr(\sigma_i)=0$, que su matriz inversa es igual a ella misma y que su transpuesta también es la misma matriz.
$$\sigma_x=\sigma_x^{-1}=\sigma_x^{T}\quad \text{, } \sigma_y=\sigma_y^{-1}=\sigma_y^{T}\quad \text{, }\sigma_z=\sigma_z^{-1}=\sigma_z^{T}$$
Otro enfoque de deducción matemática de los autovectores de las matrices de Pauli, es a partir de las propias matrices utilizando sus características y particularmente su propiedad de anticonmutación:
Además por ejemplo, armar desde la Tabla de Cayley el siguiente sistema de igualdades, donde se utiliza la diferencia de los productos cruzados de la matrices de Pauli. Ciertamente, se aplica la conmutación con la operación binaria Corchetes de Lie ([XY]=XY-YX)90:
|
| DocIRS © 1988-2026 |
| Notas Complementarias Adjuntas |