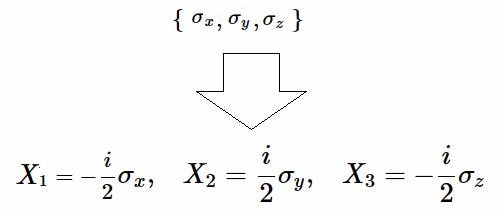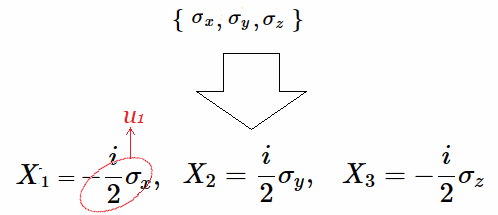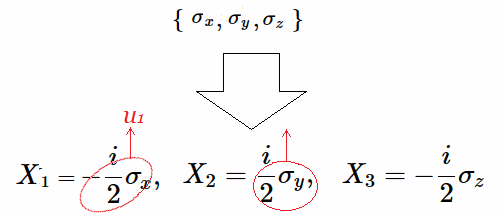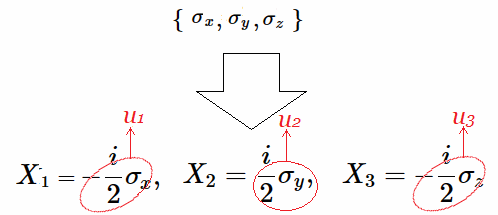Introducción
La presente nota es una síntesis88 del enfoque algebraico de la deducción de los generadores del Algebra de Lie desde las matrices de Pauli.
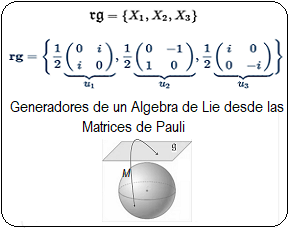
El propósito de la presentación es transformar las tres matrices de Pauli con una simple operación algebraica y obtener en tres pasos los generadores de su Algebra de Lie $\large{\mathfrak {g}}$.
En efecto, se conmutan las tres matrices de Pauli con corchetes de Lie y sus resultantes se convirtien en antihermitianas unitarias $U=\unicode{123}u_1,u_2,u_3\unicode{125}$, que al multiplicarlas por $\large{\frac{1}{2}}$ simplifican la obtención de las tres matrices generadoras infinitesimales que se han denotado como $\mathfrak{\large{rg}}=\unicode{123}X_{1},X_{2},X_{3}\unicode{125}$ (Ver Algebra de Lie ~ Generadores $SO(3)$ ). ).
Para obtener los generadores del álgebra de Lie $SU(2)$ a partir de las matrices de Pauli, simplemente se multiplican las matrices de Pauli por el imaginario complejo $\pm \large{i}$.
A continuación, se realiza un desarrollo matemático de esta síntesis algebraica mediante operaciones básicas, en tres pasos.
Síntesis en Tres Pasos
Pauli $\sigma_i \large{\longrightarrow \mathfrak {g}}$ Algebra de Lie
La nota intenta ser un complemento de comprensión de la publicación de base, teniendo en cuenta que en ese artículo se abordó la búsqueda de los generadores partiendo desde un Grupo de Lie $G \times G\longrightarrow G$.180.
A continuación, se hará uso directamente de las propiedades de estos tres operadores y transformar las tres matrices en antihermitianas181, a fin de llegar en forma algebraica a obtener los generadores del Algebra de Lie $\large{\mathfrak {g}}$ desde las Matrices de Pauli.
Recordar que el conjunto de matrices $M_{2\times 2}$ en los números complejos, bajo las operaciones ordinarias de adición matricial y multiplicación escalar, definen un espacio vectorial de cuatro dimensiones sobre el cuerpo de los números complejos. Es decir,
el conjunto de la matrices de Pauli es un caso especial del álgebra de matrices $n\times n$.
Remarcar que la multiplicación matricial asegura que el álgebra de matrices $M_{2\times 2}$ en los complejos es asociativa y no conmutativa. Estas propiedades son importantes para encontrar los generadores del Algebra de Lie asociada a la Matrices de Pauli 184.
Acción Operadores de Pauli
Esfera de Bloch19
$\sigma_x$ |
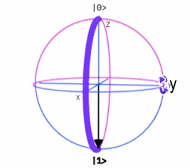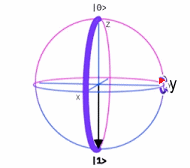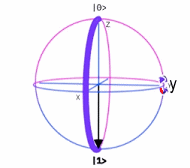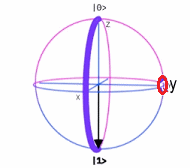
$\sigma_y$ |
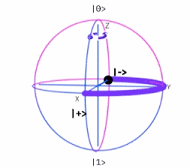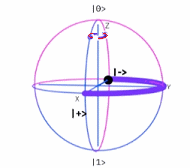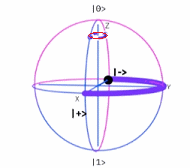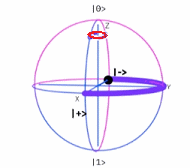
$\sigma_z$ |
Estas tres matrices de Pauli conforman una base del Algebra de Lie185 del grupo especial $SU(2)$, para el espacio vectorial complejo de todas las matrices de $2×2$, llamada Algebra de Pauli. (Obsérvese que, las matrices de Pauli son esenciales en las operaciones de qubits en computación cuántica (Ver Conceptos Matemáticos Básicos de Computación Cuántica).
Es decir, son representaciones matriciales de su operador unitario, que cumplen con la condición de que la determinante de su matriz es diferente de $0$ (toma el valor $\pm 1$), su traza $Tr(\sigma_i)=0$, que su matriz inversa es igual a ella misma y que su transpuesta también es la misma matriz.
Esta propiedad involutiva se expresa como:
$$ \sigma_x^{2}=\sigma_y^{2}=\sigma_z^{2}=I $$
$$\sigma_x=\sigma_x^{-1}=\sigma_x^{T}\quad \text{, } \sigma_y=\sigma_y^{-1}=\sigma_y^{T}\quad
\text{, }\sigma_z=\sigma_z^{-1}=\sigma_z^{T}$$
Con Determinantes:
$$
det(\sigma_x)=-1,\quad det(\sigma_y)=-1,\quad det(\sigma_z)=-1
$$
Con Trazas:
$$
Tr(\sigma_x)=0,\quad Tr(\sigma_y)=0,\quad Tr(\sigma_z)=0
$$
En otras palabras, se utilizan diversas operaciones entre las tres matrices, que al aplicarles las propiedades señaladas, permiten deducir los generadores del Algebra de Lie186 asociada a las matrices de Pauli. (Son parte de las matrices de $n × n$ cuyos elementos toman valores en el cuerpo $K = \mathbb {R} \text{ o }\mathbb{C}$).
Para simplificar el procedimiento de deducción, es necesario contar por ejemplo, con la siguiente tabla, donde se muestran los productos de la multiplicación de la matrices de Pauli:
| $$\times$$ |
$$\sigma_x$$ |
$$\sigma_y$$ |
$$\sigma_z$$ |
| $$\sigma_x$$ |
$$I$$ |
$$i\sigma_z$$ |
$$-i\sigma_y$$ |
| $$\sigma_y$$ |
$$-i\sigma_z$$ |
$$I$$ |
$$i\sigma_x$$ |
| $$\sigma_z$$ |
$$i\sigma_y$$ |
$$-i\sigma_x$$ |
$$I$$ |
$[T1]$ Tabla Multiplicación
Matrices de Pauli
En otros términos la multiplicación de las matrices de Pauli:
$$
\begin{matrix}
\sigma_x\times\sigma_y=i\sigma_z &\quad
\sigma_y\times\sigma_x=-i\sigma_z\\ \sigma_y\times\sigma_z=i\sigma_x &\quad
\sigma_z\times\sigma_y=-i\sigma_x\\ \sigma_z\times\sigma_x=i\sigma_y &\quad
\sigma_x\times\sigma_z=-i\sigma_y\\
\end{matrix}
$$
Generadores de $\mathfrak{\large g}$ desde las Matrices de Pauli
Utilizando esta tabla $[T1]$, se facilita encontrar en forma algebraica los generadores de un algebra de Lie $\mathfrak{\large g}$, asociada a las Matrices de Pauli.
Así mismo, a fin de simplificar el sistema de generadores buscado, se hará un cambio de base incorporando tres matrices auxiliares, dado que toda Algebra de Lie es por definición un espacio vectorial dotada de un conmutador que satisface ciertas propiedades. Es decir, se trata efectivamente de incluir un espacio lineal, donde sólo las constantes de estructura cambian.
Sea $U=\unicode{123}u_1,u_2,u_3\unicode{125}$ un conjunto de tres operadores complejos, hermitianos y unitarios de la forma genérica, con $b,c,d \in \mathbb {R}$ (Ver Las Matrices de Pauli Conforman una Base del Algebra de Lie de SU(2)):
| $$
\large{u_n}=\begin{pmatrix} \large{i}b & -c\large{i}+d \\ c+\large{i}d & -\large{i}b \\ \end{pmatrix}
$$ |
183 |
Luego, consideremos los siguiente tres operadores, tal que:
$$d=1 \text{ } \land \text{ } (b=c=0) \Rightarrow \large{u_1}$$
$$c=1 \text{ } \land (b=d=0) \Rightarrow \large{u_2}$$
$$b=1 \text{ } \land \text{ } (d=c=0) \Rightarrow \large{u_3}$$
Es decir,
$$
u_1=\begin{pmatrix} 0 & i \\ i & 0 \\ \end{pmatrix}\\
$$
$$
u_2=\begin{pmatrix} 0 & -1 \\ 1 & 0 \\ \end{pmatrix}\\
$$
$$
u_3=\begin{pmatrix} i & 0 \\ 0 & i \\ \end{pmatrix}\\
$$ |
[G1] |
Donde se mostrará que:
|
$$\large{u_1=-i\sigma_x}$$ |
$$\large{ u_2=i\sigma_y}$$ |
$$\large{u_3=-i\sigma_z}$$
|
|
|
|
|
$$\large{\Rightarrow}$$
|
[G1.1] |
|
|
|
|
|
|
$$\large{\sigma_x=-iu_1}$$
|
$$\large{\sigma_y=iu_2}$$ |
$$\large{\sigma_z=-iu_3}$$ |
|
De modo que, cada una de las matrices de Pauli se pueden expresar en función de $\pm \large{i} u_{n}$:
$$
-i u_1=-i\begin{pmatrix} 0 & i \\ i & 0 \\ \end{pmatrix}=\begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix}=\sigma_x\\
$$
$$
i u_2=i\begin{pmatrix} 0 & -1 \\ 1 & 0 \\ \end{pmatrix}=\begin{pmatrix} 0 & -i \\ i & 0 \\ \end{pmatrix}=\sigma_y\\
$$
$$
-i u_3=-i\begin{pmatrix} i & 0 \\ 0 & i \\ \end{pmatrix}=\begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix}=\sigma_z
$$
|
Luego considérese la conmutación de las matrices de Pauli con la operación binaria Corchetes de Lie 89, armando el siguiente sistema de igualdades:
Conmutemos matricialmente por extensión, con corchetes de Lie, las matrices de Pauli:
En resumen:
|
$$[·,·]$$ |
$\sigma_x$ |
$\sigma_y$ |
$\sigma_z$ |
|
$\sigma_x$ |
$0$ |
$2i\sigma_z$ |
$2i\sigma_y$ |
|
$\sigma_y$ |
$-2i\sigma_z$ |
$0$ |
$2i\sigma_x$ |
|
$\sigma_z$ |
$2i\sigma_y$ |
$-2i\sigma_x$ |
$0$ |
$[T2]$: Corchetes de Lie
Tabla Matrices de Pauli
En otros términos:
| $[\sigma_x \sigma_y]=\sigma_x\sigma_y - \sigma_y\sigma_x = 2\underbrace {i\sigma_z}_{u_3}=2u_3$ |
| $[\sigma_y \sigma_z]=\sigma_y\sigma_z - \sigma_z\sigma_y = 2\underbrace {i\sigma_x}_{u_1}=2u_1$ |
| $[\sigma_z \sigma_x]=\sigma_z\sigma_x - \sigma_x\sigma_z = 2\underbrace {i\sigma_y}_{u_2}=2u_2$ |
$[G2]$ |
Conmutando los operadores auxiliares $U=\unicode{123}u_1,u_2,u_3\unicode{125}$, equivalentemente a $[T2]$ resultan los siguientes generadores:
|
$$[·,·]$$ |
$u_1$ |
$u_2$ |
$u_3$ |
|
$u_1$ |
$0$ |
$2u_3$ |
$-2u_2$ |
|
$u_2$ |
$-2u_3$ |
$0$ |
$2u_1$ |
|
$u_3$ |
$2u_2$ |
$-2u_1$ |
$0$ |
$[T3]$: Corchetes de Lie
Tabla Operadores $U=\unicode{123}u_1,u_2,u_1\unicode{125}$
En otros términos, la conmutación de los operadores $U=\unicode{123}u_1,u_2,u_1\unicode{125}$:
| $\bbox[#ffffae]{[u_1 u_2]=2u_3}\qquad [u_1 u_3]=-2u_2$ |
|
| $[u_2 u_1]=-2u_3\quad \bbox[#ffffae]{[u_2 u_3]=2u_1}$ |
[G3] |
| $\bbox[#ffffae]{[u_3 u_1]=2u_2}\qquad [u_3 u_2]=-2u_1$ |
|
Representación Generadores $\large{\mathfrak {rg}}$ desde Pauli
Por lo tanto, desde las matrices de Pauli, - sin constituir un grupo -, es posible obtener algebraicamente generadores de un Algebra de Lie. En este caso, mediante un recurso algebraico utilizando $U=\unicode{123}u_1,u_2,u_1\unicode{125}$ como operadores auxiliares.

Generadores en Tres Pasos
Pauli: $\sigma_i \large{\longrightarrow \mathfrak {g}}$: Algebra de Lie
En efecto, sólo después de multiplicar los generadores resultantes de $[T2]$, por el imaginario complejo $\pm\large{\frac{i}{2}}$, es posible "normalizar" o simplificar la expresión de cada uno de los generadores infinitesimales que designaremos como {$X_1,X_2,X_3$}.
Equivalentemente cada uno de los generadores en $[G3]$ están precedidos por el factor $2$, los cuales se simplifican al multiplicar por $(\large{\frac{1}{2})}$, i.e. se transforman en generadores infinitesimales simplificados del Algebra de Lie $\large{\mathfrak {g}}$ asociado a las Matrices de Pauli.
Sea $\mathfrak{\large{rg}}=\unicode{123}X_{1},X_{2},X_{3}\unicode{125}$ su representación:
$$
X_{1}=\frac{1}{2} \underbrace{\begin{pmatrix} 0 & i \\ i & 0 \\ \end{pmatrix}}_{\large{u_1}}\\
$$
|
$$
X_2=\frac{1}{2}\underbrace{\begin{pmatrix} 0 & -1 \\ 1 & 0 \\ \end{pmatrix}}_{\large{u_2}}\\
$$
|
|
$$
X_{3}=\frac{1}{2}\underbrace{\begin{pmatrix} i & 0 \\ 0 & -i \\ \end{pmatrix}}_{\large{u_3}}
$$
|
Es decir,
$$
X_{1}=\frac{1}{2}\large{u_1},\quad
X_2=\frac{1}{2}\large{u_2},\quad
X_{3}=\frac{1}{2}\large{u_3}
$$
Luego, la matriz asociada a los valores resultantes de las conmutaciones del conjunto de
generadores infinitesimales $\mathfrak{\large{rg}}=\unicode{123} X_1, X_2, X_3\unicode{125}$ aplicando la operación corchetes de Lie se señala en la siguiente tabla.
| [·,·] |
$\mathbf {X_1}$ |
$\mathbf {X_2}$ |
$\mathbf {X_3}$ |
| $\mathbf {X_1}$ |
$0$ |
$X_3$ |
$-X_2$ |
| $\mathbf {X_2}$ |
$-X_3$ |
$0$ |
$X_1$ |
| $\mathbf {X_3}$ |
$X_2$ |
$-X_1$ |
$0$ |
Tabla Resultante de Conmutaciones $\mathfrak{\large{rg}}=\unicode{123} X_1, X_2, X_3\unicode{125}$
129
Este conjunto de tres matrices de Pauli se conecta con un Algebra de Lie $\mathfrak g$ mediante una representación que llamamos $\mathfrak{\large{rg}}$, utilizando la operación binaria, - previamente definida -, Corchetes de Lie, i.e. se satisfacen las propiedades de ser bilineal, antisimétrica y cumplir con identidad de Jacobi89.
Particularmente, los operadores $X_1$ y $X_3$ con elementos complejos y $X_2$ es un operador con elementos reales. Luego, $\large{\mathfrak {g}}$ es el conjunto de todas las matrices bidimensionales antisimétricas, que llamaremos Algebra de Lie asociada a las Matrices de Pauli.
Ver párrafo en artículo Puertas Cuánticas de Pauli ~ Base de un Algebra de Lie, donde se muestra que toda matriz unitaria $M_{2\times 2} \in \mathbb{C^n}$ se define como una combinación lineal de {$I,\sigma_x,\sigma_y,\sigma_z$}.
Por tanto, el álgebra de Lie $\mathfrak g$ asociado a las matrices de Pauli, se puede expresar como:
$$\large{\mathfrak {g}}=\unicode{123} M \in \mathbb{C^n} \text{ / }
\underbrace{M^T=-M}_{\text{Antisimetría}} \unicode{125}$$
Es necesario observar que, las matrices de Pauli {$\sigma_x,\sigma_y, \sigma_z$} se deducen construyendo operadores que actúan sobre una base de dos dimensiones179 y cumplen con las propiedades descritas previamente.
Observar también que, las Matrices de Pauli conforman una Base del Algebra de Lie de SU(2), pero no constituyen un grupo de $SO(2)$86, puesto que entre otras propiedades exigidas es que las determinantes de cada una de ellas sea igual a $1$, pero las determinantes de las matrices de Pauli son igual $-1$.
Cierre de la Demostración
En resumen, al multiplicar las matrices de Pauli por $\pm \large {i}$, se obtienen los generadores del álgebra de Lie $SU(2)$, que son esenciales para describir las propiedades algebraicas de las rotaciones en el espacio tridimensional.
Por tanto, se ha mostrado que directamente desde las Matrices de Pauli se obtienen tres generadores. Es
decir, $\text{span}\unicode{123}\mathbf {X_1, X_1, X_1}\unicode{125}$ Esta última $\large{\mathfrak {rg}}$, es la notación utilizada en este artículo.
Estos tres generadores $\large{\mathfrak {rg}}$ son las matrices unitarias:
$$
\mathfrak {\mathbf {rg}}=
\Bigg\{
\frac{1}{2} \underbrace{\begin{pmatrix} 0 & i \\ i & 0 \\ \end{pmatrix}}_{\large{u_1}},
\frac{1}{2} \underbrace{\begin{pmatrix} 0 & -1 \\ 1 & 0 \\ \end{pmatrix}}_{\large{u_2}},
\frac{1}{2} \underbrace{\begin{pmatrix} i & 0 \\ 0 & -i \\ \end{pmatrix}}_{\large{u_3}}
\Bigg\}
$$
Cuyas conmutaciones son:
 |
 |
 |
| $$[X1\text{ }X2]=X3$$ |
$$[X1\text{ }X3]=-X2$$ |
$$[X2\text{ }X1]=-X3$$ |
|
 |
 |
 |
| $$[X2\text{ }X3]=X1$$ |
$$[X3\text{ }X1]=X2$$ |
$$[X3\text{ }X2]=-X1$$ |
Por otro lado, es posible aplicar a los generadores infinitesimales $\unicode{123}X_1,X_2,X_3\unicode{125}$ con
el símbolo de Levi-Civita:
$$[X_i\text{ }X_j]=\epsilon _{ijk}X_k$$
Por ejemplo:
$$
[X_1 X_2]=\epsilon _{123}X_3 \text{, } [X_2 X_3]=\epsilon_{231} X_1 \text{, } [X1,X3]=\epsilon_{132} X_2 \dots
$$
etc. como se detalla en el artículo Definición Algebra de Lie.
|
$$
\epsilon _{ijk}=\begin{cases}+1, \\ \text{si (ijk) es (1,2,3)(2,3,1)(3,1,2)} \\\\
-1, \\ \text{si (ijk) es (3,2,1)(2,1,3)(1,3,2)} \\\\
\text{ }0, \\ \text{si i=j o j=k o k=i}\\
\end{cases}
$$
|
Símbolo Levi-Civita Generadores
Donde $\mathfrak {rg}=\unicode{123}X_1,X_2,X_3\unicode{125}$ son los generadores satisfacen la relación de conmutación del álgebra de Lie $SU(2)$, y que corresponden a las componentes de momento angular en los ejes $x, y, z$ del espacio tridimensional euclidiano respectivamente.
En síntesis, la transformación algebraica directa para obtener los generadores del algebra de Lie $\mathfrak {rg}=\unicode{123}X_1,X_2,X_3\unicode{125}$, i.e. sin recurrir a los operadores auxiliares $U=\unicode{123}u_1,u_2,u_3\unicode{125}$, es multiplicando directamente las matrices de Pauli por $\pm\large{\frac{i}{2}}$ como se muestra a continuación:

Transformación Algebraica Directa
Donde, las relaciones de conmutación de estas matrices con la operación binaria Corchetes de Lie,
resultan en $\large{\mathfrak {g}}$, que es el conjunto de matrices antisimétricas que llamaremos Algebra del Lie de Pauli
El ejercicio muestra que $\large{\mathfrak {rg}}$ es un conjunto de vectores del álgebra de Lie que pueden ser utilizados operando con los corchetes de Lie para obtener cualquier elemento del espacio.
En otrós términos,- en este caso-, todo elemento del Algebra $\large{\mathfrak {g}}$ puede ser expresado como una combinación lineal de los generadores de base $\large{\mathfrak {rg}}$. (Dado que las matrices de Pauli conforman una Base del Algebra de Lie, implica que toda matriz $M_{2×2}$ compuesta por elementos $m_{ij}\in \mathbb {C}$ de representación $SU(2)$ se puede expresar como una combinación lineal de las matrices de Pauli.)
Lo interesante es que $\large{\mathfrak {g}}$ permite estudiar las propiedades de las Matrices de Pauli de una forma más algebraica, i.e. sin recurrir a la propiedades geométricas específicas de grupos.
Finalmente, nótese que los generadores $\mathfrak{\large{rg}}=\unicode{123}X_1,X_2,X3\unicode{125}$ que se determinaron, son isomorfos a los operadores del álgebra de Lie asociados a los grupos $SO(3)$.
En efecto, las álgebras de Lie $\mathfrak {su(3)}$ y $\mathfrak {su(2)}$ son isomorfas, donde una base para $\mathfrak {su(2)}$ está dada por:
$$
\Bigg\{
X_1=\frac{1}{2} \underbrace{\begin{pmatrix} 0 & i \\ i & 0 \\ \end{pmatrix}}_{\large{u_1}},
X_2=\frac{1}{2} \underbrace{\begin{pmatrix} 0 & -1 \\ 1 & 0 \\ \end{pmatrix}}_{\large{u_2}},
X_3=\frac{1}{2} \underbrace{\begin{pmatrix} i & 0 \\ 0 & -i \\ \end{pmatrix}}_{\large{u_3}}
\Bigg\}
$$
Estos operadores están relacionadas con las matrices de Pauli por:
$$
X_{i}\longrightarrow \frac{1}{2i\sigma_i}
$$

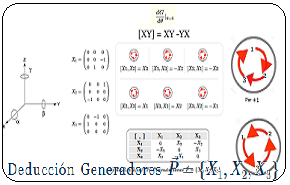
Video: Deducción Generadores $\vec P=\unicode{123}X_1,X_2,X_3\unicode{125}$ Deducción Generadores $\vec P=\unicode{123}X_1,X_2,X_3\unicode{125}$
|