¿Cuál es la relación entre las Matrices de Pauli y el Algebra de Lie?
La relación entre las tres matrices de Pauli y el Algebra de Lie es porque las matrices de Pauli forman una base para el Algebra de Lie $SU(2)$87.
Las matrices de Pauli después de multiplicarlas por $\large{i}$ se convierten en antihermitianas
91, generando transformaciones que conectan con las álgebras de Lie. Las matrices $i\sigma_1=\sigma_x=X, i\sigma_2=\sigma_y=Y, \text{ y } i\sigma_z=\sigma_z=Z$, forman una base para el Algebra de Lie. (Ver enfoque algebraico Generadores: Pauli $\sigma_i \large{\longrightarrow \mathfrak {g}}$ Algebra de Lie)
El Algebra de Lie puede tratarse como una variedad (manifold) u objeto matemático
181
, utilizado para estudiar la geometría y la estructura algebraica de los grupos de Lie (Ver Variedad Diferenciable), los cuales juegan un rol fundamental en matemática y ciencias aplicadas.
El Algebra de Lie $SU(2)$ es un ejemplo importante de Algebra de Lie, dado que es un espacio vectorial sobre los números complejos, dotado con una operación llamada Corchetes de Lie que es un conmutador que toma dos elementos del álgebra y produce otro elemento del Algebra de Lie. (Ver Deducción Generadores Infinitesimales de $SO(3)$).
Se mostrará a continuación que las matrices de Pauli son tres matrices hermíticas y unitarias que satisfacen las relaciones de conmutación necesarias para formar una base para $SU(2)$.
El Algebra de Lie $SU(2)$ está relacionado con la simetría rotacional en el espacio tridimensional (Ver Grupo de Lie-Enfoque Geométrico). En particular, el Algebra de Lie $SU(2)$ es de las rotaciones en el espacio tridimensional en torno a un eje fijo.
Las matrices de Pauli se utilizan para describir esta simetría rotacional y para construir los operadores de momento angular, que son importantes en la mecánica cuántica. (Ver Deducción de las Matrices de Pauli).
Las matrices de Pauli son importantes en la programación de circuitos cuánticos porque porque describen las operaciones de un solo qubit, que son la base de la mayoría de los circuitos cuánticos, puertas que funcionan en forma paralela y están directamente relacionadas con el principio de superposición.
Breve Introducción
La simple rotación de las puertas de
Pauli encierra una profunda y extensa parte de la física- matemática que
opera en el campo de los números reales y complejos. Su núcleo
matemático central es la simetría y la abstracción matricial, que nos inducirá a los generadores infinitesimales de un Algebra de Lie.
$$ \sigma_1=\sigma_x= \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix}
$$
$$ \sigma_2=\sigma_y= \begin{pmatrix} 0 & -i \\ i & 0 \\ \end{pmatrix}
$$
$$ \sigma_3=\sigma_z= \begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix}
$$
|
Definición y Acción de las Puertas de Pauli
Las tres matrices de Pauli31 $X, Y, Z$ son de gran utilidad en la programación de circuitos cuánticos y debajo de ellas, se encierra un gran desarrollo del Algebra Abstracta y de la Mecánica Cuántica. En efecto, las tres puertas de Pauli son un conjunto de operadores matemáticos (Ver deducción de las matrices) que se utilizan en la teoría de la información cuántica para formar una base de otras puertas cuánticas más complejas.
Haré un enfoque muy específico de las Matrices de
Pauli, orientado a entregar ciertos conceptos matemáticos básicos del Algebra de Lie, la cual sustenta en variados aspectos la programación cuántica. Nótese que las Algebras de Lie89, son más amplias que este enfoque de computación cuántica que tratamos en el presente artículo. Enfoque que sólo hemos reducido a matrices complejas de $2\times 2$. (Ver Aplicaciones ~ Definición Algebra de Lie  ) )
Algebra de Lie ~ Variedades114 Diferenciables
Estas tres matrices de Pauli son una piedra angular en la programación de circuitos cuánticos. Incluyendo la Puerta de Hadamard, - que es un operador fundamental en los algoritmos con superposición cuántica -, y que
justamente -, se obtiene de una combinación lineal de las matrices de Pauli:
$$H=\frac{1}{\sqrt{2}}(\sigma_1 + \sigma_3)=\frac{1}{\sqrt{2}}\Biggl(\begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix}+\begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix}\biggr)=\frac {1}{\sqrt{2}}
\begin{pmatrix}
1 & 1 \\
1 & -1 \\
\end{pmatrix}$$
En otros términos: $H =\frac{1}{\sqrt{2}}(X + Z)$. Esto implica que se produce una rotación sobre el eje $y$ de un ángulo $\frac{π}{2}$ e inmediatamente otra rotación de un ángulo $π$ sobre $x$. (Ver Amplitudes Equiprobables
Puerta Cuántica de Hadamard)
Situando su operación visualmente sobre la Esfera de Bloch:
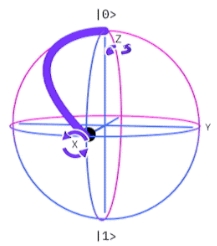
$H$ Puerta de Hadamard~Esfera de Bloch

Circuito Cuántico~IBM Composer
Puerta Cuántica $X$ análoga a NOT
Debemos buscar un operador $X$, tal que:
i) $|0〉 → |1〉$ y $|1〉 → |0〉$
ii) Lineal: $α_0 |0〉 + α_1 |1〉 → α_1 |1〉 + α_0|0〉$
ii) Sea unitario ($|α_0|^{2} + |α_1|^{2} = 1$).
Es decir, esta puerta Pauli $X$ , opera como una puerta $NOT$, cambia de un estado básico a otro (viceversa). La puerta $NOT$ es equivalente a la puerta $RX$ (del IBM Quantum Composer), para el ángulo $\pi$ radianes de rotación en torno al eje de las $x$.
| El operador es: |
|
|
$
\sigma_1=\sigma_x=X=
\begin{pmatrix}
0 & 1 \\
1 & 0 \\
\end{pmatrix}
$
|
$|\psi〉=\alpha_0|0〉+\alpha_1|1〉=\left[\begin{matrix}\alpha_0\\\alpha_1 \end{matrix}\right]$
|
Aplicamos el operador $X$
|
$
X=
\begin{pmatrix}
0 & 1 \\
1 & 0 \\
\end{pmatrix}
\left[\begin{matrix}\alpha_0\\\alpha_1 \end{matrix}\right]=
\begin{pmatrix}
0\alpha_0 & 1\alpha_1 \\
1\alpha_0 & 0\alpha_1 \\
\end{pmatrix}
=\left[\begin{matrix}\alpha_1\\\alpha_0 \end{matrix}\right]
$
|
∴ Su acción sobre un qubit es:
$α_0|0〉 + α_1|1〉\longrightarrow$$X$$\longrightarrow α_1|1〉 + α_0|0〉$
La transformación $X$ se desplaza a lo largo del intervalo en la esfera de Bloch sobre la superficie de la esfera desde $|0〉$ hasta $|1〉$, rotando valores alrededor del eje $x$.
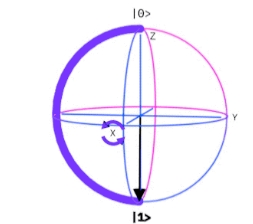
$X$ ibm quantum experience-fuente gates glossary
|
|
Puerta Cuántica $Y$
| El operador es equivalente a una rotación de $\pi$ radianes en torno al eje de la $y$: |
|
$
\sigma_2=\sigma_y=Y=
\begin{pmatrix}
0 & -i \\
i & 0 \\
\end{pmatrix}
$
|
Aplicamos el operador $Y$
$
Y|0〉=
\begin{pmatrix}
0 & -i \\
i & 0 \\
\end{pmatrix}
\left[\begin{matrix} 1\\0 \end{matrix}\right]
=\left[\begin{matrix} 0\\-i \end{matrix}\right]
$
$
Y|1〉=
\begin{pmatrix}
0 & -i \\
i & 0 \\
\end{pmatrix}
\left[\begin{matrix} 0\\1 \end{matrix}\right]
=\left[\begin{matrix} -i\\0 \end{matrix}\right]
$
|
∴ Su acción sobre un qubit es:
La transformación $Y$ se desplaza a lo largo del intervalo en la esfera de Bloch sobre la superficie de la esfera desde $|0〉$ hasta $|1〉$, rotando valores alrededor del eje $y$.
$Y$ ibm quantum experience-fuente gates glossary
|
Puerta Cuántica $Z$
La puerta $Z$ es equivalente a una rotación de $\pi$ radianes en torno al eje de la $z$ y viene definida por la matriz (unitaria):
$
\sigma_3=\sigma_z=Z=
\begin{pmatrix}
1 & 0 \\
0 & -1 \\
\end{pmatrix}
$
Su accion es:
$|0〉\longrightarrow$$Z$$\longrightarrow |0〉$
$|1〉\longrightarrow$$Z$$\longrightarrow -|1〉$
Es decir, la transformación lineal $Z$, cambia de signo la amplitud cuando
se aplica al estado del qubit $|1〉$ y lo deja igual cuando se opera con el estado del qubit $|0〉$.
$∴\quad$Su acción sobre un qubit es:
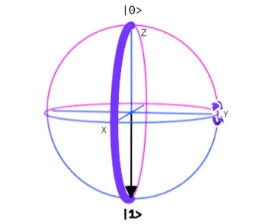
La transformación $Z$ se desplaza a lo largo del intervalo en la esfera de Bloch sobre la superficie de la esfera desde $|0〉$ hasta $|1〉$, rotando valores alrededor del eje $z$.
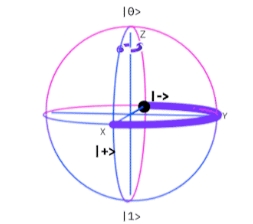
$Z$ ibm quantum experience-fuente gates glossary
Equiparse con Más Matemática
Para aquellos que se están
equipando con más matemática, se hace necesario mencionar el Algebra de
Lie81
y tratar las propiedades de grupo. Cualidades que son un tremendo
sustento matemático detrás de esas tres puertas cuánticas utilizadas
permanentemente en la programación de circuitos. En efecto, veremos que
las matrices de Pauli junto a la matriz Identidad, constituyen una base vectorial del Algebra de Lie del grupo especial unitario de simetría $SU(2)$87 (dimensión 2)
Se hace hincapié que las transformaciones de Pauli sí conforman
un Algrebra de Lie, dado que cumple con las propiedades requeridas bajo
las operaciones binarias estándar. Sin embargo, las Matrices de Pauli no
cumplen las propiedades suficientes para constituir un Grupo. (Por tanto,
tampoco un Grupo de Lie86).
En general, los programadores en sus algoritmos de computación cuántica
utilizan las Puertas de Pauli frecuentemente, - poniendo y sacando
objetos sobre los cables del circuito, ejecutando y probando su
algoritmo -, pero sólo conociendo la acción de dichas transformaciones
en forma operativa.

Vista del Editor Circuit Composer de IBM
Representación Exponencial de la Matrices de Pauli
En este párrafo se muestran las transformaciones de forma exponencial de las tres matrices de Pauli, mediante la expresión:
$$\large{e}^{i\theta\sigma_k}\longrightarrow I\cos(\theta) + i\sigma_k\sin(\theta)$$
En el tratamiento con matrices de Pauli $\unicode{123}\large{\sigma_x,\sigma_y,\sigma_z}\unicode{125} \equiv \unicode{123}\large{\sigma_1,\sigma_2,\sigma_3}\unicode{125}$ es importante incluir la transformación exponencial mediante series de Taylor.
Esta expansión de la función matricial exponencial de rotación se aplica para todo operador de Pauli en su forma canónica $\sigma_k \text{ con } k=\unicode{123}1,2,3\unicode{125} \lor \unicode{123}k=x,y,z\unicode{125}$.
En efecto, se demuestra desde la serie de Taylor de $\large{e}^A$, junto a la propiedad antisimétrica de los corchetes de Lie ($[XY]=-[YX]$) conforman una relación simple mediante el mapeo exponencial. (Serie que es convergente para matrices $Mn×n\in SO(n)$, tanto en $\mathbb R$ como $\mathbb {C} \rightarrow $ Ver Definición Alebra de Lie)
La definición del exponencial elevado a potencias de una matriz $A$, utilizando las operaciones binarias ordinarias es semejante a las series definidas sobre el campo de los reales o complejos. Sólo que el neutro multiplicativo $1$, matricialmente es la matriz idéntica $I$. (Ver Grupo de Lie Enfoque Exponencial)
$$
\large{e}^A=I+ A + \frac{1}{2}A^2 + \frac{1}{3!}A^3+\frac{1}{4!}A^4 + \frac{1}{5!}A^5 + \frac{1}{6!}A^6+\frac{1}{7!}A^7+ \cdots = \sum_{k=0}^{\infty} \frac{1}{k!}A^k \qquad\quad [L7]
$$
Luego, sea $A={i\sigma_k{(\frac{\phi}{2})}}$, sustituyendo en [L7], la expansión en Taylor se expresa de siguiente forma:
$\large{e^{i\sigma_k{(\frac{\phi}{2})}}}=
{i\sigma_k{(\frac{\phi}{2})}} + \frac{1}{2}({i\sigma_k{(\frac{\phi}{2})}})^2
+ \frac{1}{3!}({i\sigma_k{(\frac{\phi}{2})}})^3 + \frac{1}{4!}({i\sigma_k{(\frac{\phi}{2})}})^4
+ \frac{1}{5!}({i\sigma_k{(\frac{\phi}{2})}})^5 + \frac{1}{6!}({i\sigma_k{(\frac{\phi}{2})}})^6
+\frac{1}{7!}({i\sigma_k{(\frac{\phi}{2})}})^7+ \cdots\cdots$
$$
=\sum_{k=0}^{\infty} \frac{1}{k!}({i\sigma_k{(\frac{\phi}{2})}})^k \qquad\quad [L7.1]
$$
De donde, se pueden reacomodar los términos, separando la parte real de la parte compleja, para obtener la serie de la funciones $sin(\frac{\phi}{2}) \text{ y } cos(\frac{\phi}{2})$, dado que las potencias del imaginario $\large{i}^k$ irán tomado valores $\unicode{123}\large{\pm i, \pm 1}\unicode{125}$ en la expansión.
Esto permite escribir el operador de rotación matricial general en función de las matrices de Pauli de la siguiente manera:
| $$\Large{e}^{\large{i\sigma_k(\frac{\phi}{2})}}=$$ |
$$\underbrace{I·(1 - \frac{1}{2} \sigma_k^{2}(\frac{\phi}{2})^{2} + \frac{1}{4!}\sigma_k^{4}(\frac{\phi}{2})^{4} -\frac{1}{6!}\sigma_k^{6}(\frac{\phi}{2})^{6}+\cdots)} $$ |
+ |
$$\large{i}·\underbrace{(\frac{1}{1!}\sigma_k(\frac{\phi}{2})^1 - \frac{1}{3!}\sigma_k^{3}(\frac{\phi}{2}){^3} + \frac{1}{5!}\sigma_k^{5}(\frac{\phi}{2})^{5}-\frac{1}{7!}\sigma_k^{7}(\frac{\phi}{2})^{7} + \cdots)}$$ |
| |
$$I·\cos(\frac{\phi}{2})$$ |
+ |
$$\large{i}\sigma_k· \sin(\frac{\phi}{2})$$ |
Por tanto, al especificar el operador general de rotación para una rotación de $\Large{\phi=\pi}$:
$$\require{cancel} \large{e}^{\large{i\sigma_k(\frac{\pi}{2})}}=I·\cancelto{0}{\cos(\frac{\pi}{2})} + \large{i}\sigma_k· \cancelto{1}{\sin(\frac{\pi}{2})}$$
Dado que $\large{\cos(\frac{\pi}{2})=0\quad\text{ y }\quad \sin(\frac{\pi}{2})=1}$, se deduce que:
$$\bbox[8px,border:1px solid #000000]{\Large{e}^{\large{i\sigma_k(\frac{\phi}{2})}}=\large{i \sigma_k}}\qquad\quad[L7.2]$$
$$\Large {\Rightarrow} $$
| $$\large{e}^{\large{i\sigma_x(\frac{\pi}{2})}}$$ |
$$=\large{i}\sigma_x$$ |
$$=\large{i}\begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix}$$ |
$$=\large{\begin{pmatrix} 0 & i \\ i & 0 \\ \end{pmatrix}}$$ |
| |
| $$\large{e}^{\large{i\sigma_y(\frac{\pi}{2})}}$$ |
$$=\large{i}\sigma_y$$ |
$$=\large{i}\begin{pmatrix} 0 & -i \\ i & 0 \\ \end{pmatrix}$$ |
$$=\large{\begin{pmatrix} 0 & 1 \\ -1 & 0 \\ \end{pmatrix}}$$ |
| |
| $$\large{e}^{\large{i\sigma_z(\frac{\pi}{2})}}$$ |
$$=\large{i}\sigma_z$$ |
$$=\large{i}\begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix}$$ |
$$=\large{\begin{pmatrix} i & 0 \\ 0 & -i \\ \end{pmatrix}}$$ |
$$\Large {\Rightarrow} $$
Multiplicando $[L7.2]$ por $\Large{\frac{1}{i}}$, a fin de obtener sólo las $\sigma_k$, se tiene que:
$$
\require{cancel}
\Large{\frac{e^{i\sigma_k{(\frac{\phi}{2})}}}{i}=\cancel{i}\frac{\sigma_k}{\cancel{i}}=\sigma_k \Rightarrow -ie^{i\sigma_k{(\frac{\phi}{2})}}=\sigma_k}$$,
dado que $\Large {\frac{1}{i}=-i}$
$$\Large {\Rightarrow} $$
| $$ \large{-i} e^{i\sigma_x{(\frac{\phi}{2})}}= \sigma_1=\sigma_x= \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix}
$$ |
 |
| |
| $$ \large{-i} e^{i\sigma_y{(\frac{\phi}{2})}}= \sigma_2=\sigma_y= \begin{pmatrix} 0 & -i \\ i & 0 \\ \end{pmatrix}
$$ |
 |
| |
| $$ \large{-i} e^{i\sigma_z{(\frac{\phi}{2})}}= \sigma_3=\sigma_z= \begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix}
$$ |
 |
Otro Enfoque Exponencial Equivalente
Equivalentemente, se puede abordar la exponenciación de la Matrices de Pauli a partir de la ecuación en forma polar del exponencial de un número complejo:
$$\large{e}^{\large{i\sigma_k(\frac{\phi}{2})}}=\cos(\frac{\phi}{2}) + i\sin(\frac{\phi}{2})$$
Utilizando propiedades de la matrices de Pauli como la potencias pares $\sigma_x^{2}=\sigma_y^{2}=\sigma_z^{2}=I$, i.e. $\sigma_k ^{2n}=I$ y las potencias impares $\sigma_k^{2n+1}= \sigma_k^{2n}\sigma_k=I\sigma_k=\sigma_k$, donde $n \in \mathbb{N}$ (en este caso los enteros positivos).
Las funciones trigonométricas senos y cosenos, son expandibles como series de Taylor con ángulos infinitesimales.
$$sin(\frac{\phi}{2})=\frac{1}{1!}(\frac{\phi}{2})^1 - \frac{1}{3!}(\frac{\phi}{2}){^3} + \frac{1}{5!}(\frac{\phi}{2})^{5}-\frac{1}{7!}(\frac{\phi}{2})^{7} + \cdots=\sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)!}(\frac{\phi}{2})^{2n+1}$$
$$cos(\frac{\phi}{2})=1 - \frac{1}{2}(\frac{\phi}{2})^{2} + \frac{1}{4!}(\frac{\phi}{2})^{4} -\frac{1}{6!}(\frac{\phi}{2})^{6}+\cdots=\sum_{n=0}^{\infty} \frac{(-1)^n}{2n!}(\frac{\phi}{2})^{2n}$$
Luego, de acuerdo a la expresión $[L7.1]$:
$$\large{e^{i\sigma_k{(\frac{\phi}{2})}}}=\sum_{n=0}^{\infty} \frac{(i\frac{\phi}{2})^{n}}{n!}\sigma_k^n$$
Separando las potencias pares de las impares de la sumatoria y sustituyendo por las igualdades $\large{i^{2n}=(-1)^n,\quad (i)^{2n+1}=(-1)^n\large i}$, se tiene:
$$
\large{e^{i\sigma_k{(\frac{\phi}{2})}}}=\sum_{n=0}^{\infty} \frac{(i)^{2n}(\frac{\phi}{2})^{2n}} {(2n)!}\sigma_k^{2n}
+\sum_{n=0}^{\infty} \frac{(i)^{2n+1}(\frac{\phi}{2})^{2n+1}}{(2n+1)!}\sigma_k^{2n+1}
$$
$$
\large{e^{i\sigma_k{(\frac{\phi}{2})}}}=I·\underbrace{\bbox[8px,border:1px solid #e2e2e2]{\sum_{n=0}^{\infty} \frac{(-1)^n}{2n!}(\frac{\phi}{2})^{2n}}}_{\Large { \cos(\frac{\phi}{2})}}
+ \large{i} · \sigma_k \underbrace{\bbox[8px,border:1px solid #e2e2e2]{\sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)!}(\frac{\phi}{2})^{2n+1}}}_{\Large {\sin(\frac{\phi}{2})}}
$$
$$\Large {\Rightarrow} $$
Para una rotación de $\Large{\phi=\pi}$:
$$\require{cancel} \large{e}^{\large{i\sigma_k(\frac{\pi}{2})}}=I·\cancelto{0}{\cos(\frac{\pi}{2})} + \large{i}\sigma_k· \cancelto{1}{\sin(\frac{\pi}{2})}$$
Dado que $\large{\cos(\frac{\pi}{2})=0\quad\text{ y }\quad \sin(\frac{\pi}{2})=1}$, se deduce que:
$$\bbox[8px,border:1px solid #000000]{\Large{e}^{\large{i\sigma_k(\frac{\phi}{2})}}=\large{i \sigma_k}}\qquad\quad[L7.2]$$
Matrices de Pauli ~ ¿Base Espacio Vectorial?
Ciertamente, las
transformaciones cuánticas de Pauli conforman una base para el espacio
vectorial complejo de todas las matrices de $2\times2$ de Grupo Especial Unitario de Dimensión $2$, $SU(2)$, dado que:
i) Son linealmente independientes. (La prueba muestra que no es
posible expresar cualquiera de una de las matrices como combinación
lineal de las otras dos).
Equivalentemente, se verifica que existen
$4$ números complejos $\alpha_0,\alpha_1,\alpha_2,\alpha_3 \in \mathbb C$ tal que:
$$\alpha_0 I + \alpha_1 \sigma_1 +
\alpha_2 \sigma_2 + \alpha_3 \sigma_3 = 0 ⇔ \alpha_i=0 \quad \forall
i=0,1,2,3$$
$$M = \begin{pmatrix}
m_{11}& m_{12} \\ m_{21}& m_{22} \\ \end{pmatrix}=\begin{pmatrix}
0& 0 \\ 0& 0 \\ \end{pmatrix}\Rightarrow\alpha _0 I+\alpha_1
\sigma_1 + \alpha_2 \sigma_2 + \alpha_3 \sigma_3=0\qquad\text{(matriz 0)}$$
$$\Rightarrow \alpha_i =0, \text{ para } i=0,1,2,3\quad $$
Es decir:(Ver $[4.2]$),
$$\begin{pmatrix} \alpha_0 + \alpha_3 & \alpha_1-i\alpha_2 \\ \alpha_1+i\alpha_2 &
\alpha_0-\alpha_3 \end{pmatrix}=\begin{pmatrix} 0 & 0 \\ 0 &
0 \end{pmatrix}$$
Por lo tanto, $\forall \alpha_i =0$ cuando $M$ es la matriz $0$
ii) Toda matriz compleja $2×2$ puede ser expresada como una
combinación de las matrices del conjunto $\unicode{123}I,\sigma_i\unicode{125}$
con $i=1,2,3$ (Ver
Combinación Lineal de Matrices de
Pauli).
Las Matrices de Pauli Conforman una Base del Algebra de Lie (de $SU(2)$)
Nota.-
Las matrices $\unicode{123}I,\sigma_1,\sigma_2,\sigma_3\unicode{125}$, forman un conjunto completo de matrices, siendo una base del espacio de las matrices Hermitianas $2×2$. Las matrices de Pauli son proporcionales a los generadores del Grupo $SU(2)$, grupo que conecta, - mediante el grupo $SO(3)$ de rotaciones -, con un Algebra de Lie, utilizando la operación binaria Corchetes de Lie. (Ver Artículo: Generadores $SO(3)$ y Video: Deducción Generadores $\mathfrak{\large{rg}}=\unicode{123}X_1,X_2,X_3\unicode{125}$. y Video: Deducción Generadores $\mathfrak{\large{rg}}=\unicode{123}X_1,X_2,X_3\unicode{125}$.
Luego mostremos $(ii)$ i.e. $\forall M_{2 \times 2} \text{ unitaria } \in \mathbb C$ se puede
expresar como una combinación lineal de $\unicode{123}I,\sigma_1,\sigma_2,\sigma_3\unicode{125}$.
En otros términos, probar que las matrices de Pauli conforman una Base del Algebra
de Lie, implica que toda matriz $M$ de $2 \times 2$ compuesta por elementos $m_{ij} \in \mathbb C$ de representación $SU(2)$ se puede expresar como una combinación lineal de las matrices de Pauli.
Luego, existen coeficientes $\alpha_i,\text{ con }i=0,1,2,3$ en los complejos que permiten esa combinación líneal:
$$M = \begin{pmatrix}
m_{11}& m_{12} \\ m_{21}& m_{22} \\ \end{pmatrix}=\alpha _0 I+\alpha_1
\sigma_1 + \alpha_2 \sigma_2 + \alpha_3 \sigma_3\qquad\qquad[4.1]$$
$$\text{Donde } \alpha_i \in \mathbb C, \text{ con } i=0,1,2,3\quad
(\sigma_0=I)$$
$\Rightarrow$
$$\begin{pmatrix} m_{11}& m_{12} \\ m_{21}& m_{22} \\ \end{pmatrix}=\alpha
_0 \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ \end{pmatrix} + \alpha_1 \begin{pmatrix}
0 & 1 \\ 1 & 0 \\ \end{pmatrix} + \alpha_2 \begin{pmatrix} 0 & -i \\ i
& 0 \\ \end{pmatrix} + \alpha_3 \begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix}
$$
$\Rightarrow$ $$ \begin{matrix} m_{11}=\alpha_0+\alpha_3 \\
m_{12}=\alpha_1-i\alpha_2 \\ m_{21}=\alpha_1+i\alpha_2 \\
m_{22}=\alpha_0-\alpha_3 \end{matrix} \qquad\quad[4.2] $$
Por lo tanto, $$\forall M\in SU(2)\quad\exists \alpha_i \in \mathbb C \text{ / }
M=\sum_{i=0}^3 \alpha_i \sigma_i$$
Despejando los $\alpha_i$ en función de los $m_{ij}
\Rightarrow$
$$
\begin{matrix}
\alpha_0=\frac{1}{2}(m_{11}+m_{22})\\
\alpha_1=\frac{1}{2}(m_{12}+m_{21})\\
\alpha_2=\frac{1}{2}i(m_{12}-m_{21})\\
\alpha_3=\frac{1}{2}(m_{11}-m_{22})\\
\end{matrix}
\qquad\qquad[4.3]
$$
También la matriz $M$ se puede escribir como $M = A+\mathbf {\mathit{i}} B$, donde tanto $A$ como $B$ son matrices hermitianas, i.e. $M=(M^{T})^{*}$. Entonces, existen números reales únicos $\alpha_0,\alpha_1,\alpha_2,\alpha_3,\beta_0,\beta_1,\beta_2,\beta_3$, donde:
$$A=\alpha_0 I + \sum_i \alpha_i \sigma_i\\\text{y}\\$$
$$B=\beta_0 I+\sum_i {\beta_i\sigma_i}\\\text{por lo tanto}\\$$,
$$M=(\alpha_0+\mathbf {i}\beta_0)I+\sum_i(\alpha_i+ \mathbf {i}\beta_i)\sigma_i$$
Es decir, las matrices de Pauli junto con la matriz identica $I$ expanden el
espacio vectorial complejo de las matrices complejas de $2 \times 2$ constituyendo una base. Donde la dimensión (compleja) de este espacio vectorial es $4$.
Matrices de Pauli ~ Generadoras Algebra de Lie
Las matrices de Pauli no son generadores del grupo de Lie $SU(2)$, no obstante una vez que se multiplica por el imaginario $\large i$, se transforma en los llamados generadores infinitesimales de un Algebra de Lie. (Ver Deducción Generadores Infinitesimales de SO(3) ~ Complemento #1 Definición Algebra de Lie)

Generadores en Tres Pasos
Pauli: $\sigma_i \large{\longrightarrow \mathfrak {g}}$: Algebra de Lie
En efecto, los elementos del álgebra de Lie $\mathfrak {su(2)=g}$ de $SU(2)$, para los elementos $X$ del mapeo exponencial $t\mapsto \large{e}^{(tX)}$ produce un subgrupo de uniparámetrico del Grupo de Lie.
Bajo esta relación, la determinante de las matrices de Pauli no juega un rol significativo. Lo relevante es que la matrices son hermitianas. Nótese que la multiplicación por $\large i$ las convirtió en antihermitianas, como así mismo el mapeo exponencial las transformó en matrices unitarias. Por otro lado, tienen traza cero y a casua del mapeo exponencial se convierten en matrices de determinante igual $1$.
Se puede decir que las matrices de Pauli generan el espacio vectorial real de las matrices hermitianas sin trazos.
De ese modo cada elemento de $SU(2)$ es la imagen bajo el mapeo exponencial de una combinación lineal real de los múltiplos por $\large i$ de las matrices de Pauli.
Ejemplo Algebra de Lie con Matrices $2\times 2$ con Pauli:
Experimentemos con el siguiente ejercicio en $SU(2)$, con un simulador que genera matrices de $2\times 2$,- sólo presionando el botón "Random"- , cuyos elementos son valores enteros aleatorios entre -100 y 100, para los coeficientes $\alpha_0,\alpha_1,\alpha_2,\alpha_3$ (Ver $[4.2]$). Cualquier matriz de $2\times 2$ generada, se escribirá en función de las matrices de Pauli y la matriz identidad.
Simulador Matrices $2\times 2$
Delta de Kronecker
Efectivamente, estas tres
transformaciones se pueden compactar en una sola matriz,
aplicando un parámetro de control llamado Delta de Kronecker
y denotado con el símbolo griego $\delta_{ij}$.
Este
parámetro Delta de Kronecker, es necesario mencionarlo y
mostrarlo, porque jugará un rol importante en determinados
circuitos que irán apareciendo en el avance de la programación
cuántica.
De la expresión $[4.2]$, se deduce este
parámetro $\delta_{ij}$ que se construye en función de dos
variables, que pueden tomar valores $1$ o $0$.
A continuación se mostrará que según el valor que adquiera
$\delta_{ij}$, se puede obtener cualquiera de las tres matrices
o utilizar algebraicamente esta reducción, a fin de sintetizar
el uso de los atributos de rotación y simetría que se generan
con estas transformaciones.
En efecto, $\delta_{ij}$ es
una función de control, dado que es $1$ si las variables son
iguales y $0$ en caso contrario.
$$ \delta_{ij} = \begin{cases}
0, & \text{if i≠ j} \\ 1, & \text{if i=j} \end{cases} $$
|
|
De modo que la representación de cada matriz de Pauli $\sigma_i$
se puede expresar en función del Delta de Kronecker con la
siguiente matriz compacta:
|
$$ \sigma_i= \begin{pmatrix} \delta_{i3} & \delta_{i1}-i·\delta_{i2}
\\ \delta_{i1}+i·\delta_{i2}&-\delta_{i3} \\ \end{pmatrix} $$
Donde $i=1,2,3 \quad\text{ i.e. }\quad\sigma_1,\sigma_2,\sigma_3$
son igual que $\sigma_x,\sigma_y\sigma_z$ respectivamente. (Así
mismo $i=\sqrt{-1}$). |
|
Características de las Matrices de Pauli
Las
matrices de Pauli corresponden a las características de matrices
de rotación que conforman una base del Algebra de Lie,
del grupo especial SU(2). En este caso, corresponden al conjunto
de las matrices unitarias de $2 \times 2$ definidas sobre los
complejos con las operaciones binarias ordinarias. Nótese que
las tres matrices de Pauli no constituyen en sí un Grupo,
pero se puede extender el conjunto de las matrices de Pauli para
construir un Grupo de 8 matrices.
La
Matrices de Pauli No Constituyen un Grupo El
conjunto de matrices de Pauli unido a la matriz Identidad,
$P=\unicode{123}I,\sigma_i\unicode{125}$, no constituye un
grupo porque al multiplicar elementos del conjunto se
obtienen elementos que no forman parte del conjunto $P$.
Es decir, $P$ no es un conjunto cerrado para la
operación de multiplicación matricial, dado que $\exists x,y\in
P \text{ / }x·y\notin P$. Por tanto, $P$ no es un grupo. 80
$$ \begin{matrix} \sigma_1\sigma_2=i\sigma_3 &\quad
\sigma_2\sigma_1=-i\sigma_3\\ \sigma_2\sigma_3=i\sigma_1 &\quad
\sigma_3\sigma_2=-i\sigma_1\\ \sigma_3\sigma_1=i\sigma_2 &\quad
\sigma_1\sigma_3=-i\sigma_2\\ \end{matrix} $$
De donde
se puede deducir cuales son los elementos faltantes para
configurar un conjunto cerrado, que permita constituir un
Grupo 79.
G={I,-I,
σ1, -σ1,
iσ2, -iσ2,
σ3, -σ3}
Extensión Matrices
de Pauli Conformación de Grupo A continuación
construimos la tabla de operaciones del grupo extendido $G$,
dónde se puede observar que es cerrado, que cada tiene
identidad y que cada elemento dentro de la tabla tiene su
inverso.
Aún más, con el grupo extendido $G$ es posible obtener todas las rotaciones de $\pi$ en torno a los ejes de coordenadas sobre el plano cartesiano. Claramente, $G$ no es Abeliano. (Por ejemplo, $\sigma_1\sigma_3\neq\sigma_3\sigma_1$).
Nótese que las matrices que conforman el grupo extendido $G$ están compuestas sólo por elementos reales $\unicode{123}-1,0,1\unicode{125}$, dado que hemos sacado como factor el número imaginario $i\in \mathbb C$ de las matrices $\pm\sigma_2$.
Tabla de Operaciones del Grupo G
|
$\mathbf\times$ |
$I$ |
$-I$ |
$\sigma_1$ |
$-\sigma_1$ |
$i\sigma_2$ |
$-i\sigma_2$ |
$\sigma_3$ |
$-\sigma_3$ |
| $I$ |
$I$ |
$-I$ |
$\sigma_1$ |
$-\sigma_1$ |
$i\sigma_2$ |
$-i\sigma_2$ |
$\sigma_3$ |
$-\sigma_3$ |
| $-I$ |
$-I$ |
$I$ |
$-\sigma_1$ |
$\sigma_1$ |
$-i\sigma_2$ |
$i\sigma_2$ |
$-\sigma_3$ |
$\sigma_3$ |
|
$\sigma_1$ |
$\sigma_1$ |
$-\sigma_1$ |
$I$ |
$-I$ |
$i\sigma_3$ |
$-i\sigma3$ |
$-i\sigma2$ |
$i\sigma2$ |
|
$-\sigma_1$ |
$-\sigma_1$ |
$\sigma_1$ |
$-I$ |
$I$ |
$-i\sigma3$ |
$i\sigma3$ |
$i\sigma2$ |
$-i\sigma2$ |
|
$i\sigma_2$ |
$i\sigma_2$ |
$-i\sigma_2$ |
$-i\sigma_3$ |
$i\sigma_3$ |
$I$ |
$-I$ |
$i\sigma_1$ |
$-i\sigma_1$ |
|
$-i\sigma_2$ |
$-i\sigma_2$ |
$i\sigma_2$ |
$\sigma_3$ |
$-\sigma_3$ |
$-I$ |
$I$ |
$-\sigma_1$ |
$\sigma_1$ |
|
$\sigma_3$ |
$\sigma_3$ |
$-\sigma_3$ |
$i\sigma_2$ |
$-i\sigma_2$ |
$-i\sigma_1$ |
$i\sigma_1$ |
$I$ |
$-I$ |
|
$-\sigma_3$ |
$-\sigma_3$ |
$\sigma_3$ |
$-i\sigma_2$ |
$i\sigma_2$ |
$-i\sigma_1$ |
$i\sigma_1$ |
$-I$ |
$I$ |
Síntesis: Propiedades Puertas de Pauli y el Algebra de Lie
En síntesis, las tres transformaciones de Pauli $\unicode{123}\sigma_x,\sigma_y,\sigma_z\unicode{125}$,
- son puertas cuánticas involutivas ($I^{2}=X^{2}=Y^{2}=Z^{2}=-iXYZ=I$) y además Hermíticas o Hermitianas, i.e. $M=(M^{T})^{*}\Rightarrow
M$ es igual a su transpuesta conjugada
y se representan en rotaciones $\pi$ radianes en torno al eje de su
propio nombre sobre la esfera de Bloch, i.e. en el espacio euclidiano
tridimensional $R^{3}$88.
Las tres son representaciones matriciales de su operador unitario, que cumplen con la condición de que la determinante de su matriz es diferente de $0$ (toma el valor $\pm 1$), su traza $Tr(\sigma_i)=0$, que su matriz inversa es igual a ella misma y que su transpuesta también es la misma matriz.
Esta propiedad involutiva se expresa como:
$$ \sigma_x^{2}=\sigma_y^{2}=\sigma_z^{2}=I $$
$$\sigma_x=\sigma_x^{-1}=\sigma_x^{T}\quad \text{, } \sigma_y=\sigma_y^{-1}=\sigma_y^{T}\quad
\text{, }\sigma_z=\sigma_z^{-1}=\sigma_z^{T}$$.
| $$ Det(\sigma_x)= \begin{vmatrix} 0 & 1 \\ 1 & 0 \\ \end{vmatrix}=-1,\quad
$$ |
$$ Det(\sigma_y)= \begin{vmatrix} 0 & -i \\ i & 0 \\ \end{vmatrix}=-1,\quad
$$ |
$$ Det(\sigma_z)= \begin{vmatrix} 1 & 0 \\ 0 & -1 \\ \end{vmatrix}=-1
$$ |
Matemáticamente, esto significa que las Matrices de Pauli,
corresponden a las características de matrices de rotación que conforman
una base para el Algebra de Lie, del grupo SU(2). En este caso al
conjuntos de las matrices unitarias de $2 \times 2$ definidas sobre los
complejos con las operaciones binarias ordinarias. Adicionalmente, $G=\unicode{123}I,-I,\sigma_1,-\sigma_1,i\sigma_2,-i\sigma_2,\sigma_3,-\sigma_3\unicode{125}$,
es un grupo unitario y Hermítico
79
definido sobre un espacio de Hilbert.
La matriz identidad $I$ es
como la matriz neutra o $0$ de Pauli, también se le denota como
$\sigma_0$ (Ver Tabla de Operaciones de G).
Nótese que $G$ es un grupo ortogonal unitario no abeliano,
dado matrices de Pauli no son conmutativas. Por ejemplo, $\sigma_1
\sigma_3\neq \sigma_3 \sigma_1$. En efecto:
$$ \sigma_1 \sigma_3=
\begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix} \begin{pmatrix} 1 & 0 \\
0 & -1 \\ \end{pmatrix} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \\ \end{pmatrix}
$$
$$ \sigma_3 \sigma_1= \begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix}
\begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix} = \begin{pmatrix} 0 & 1
\\ -1 & 0 \\ \end{pmatrix} $$
$\Rightarrow$
$$ \begin{pmatrix} 0 & -1 \\ 1 & 0 \\ \end{pmatrix} \neq \begin{pmatrix}
0 & 1 \\ -1 & 0 \\ \end{pmatrix} $$
En efecto, sea $G$ un grupo definido en los complejos (con las
operaciones de adición ordinaria de vectores y multiplicación de
matrices), tal que es el conjunto de todas las matrices $M$ de
$2\times2$ cuya determinante $Det(M)\pm-1$ y la inversa de $M^{-1}=M^{T}$,
i.e. la inversa de $M$ es igual a su matriz transpuesta. (Una matriz
ortogonal es una matriz real cuya inversa es igual a su transposición).
En otros simples términos, $G=\unicode{123}M\in SU(2)\text{/ Det}(M)\pm
1 \land M^{-1}=M^{T}\unicode{125}$, i.e. $M^{T}M^{-1}=I$ (extendido a 8
matrices, i.e. el conjunto $G=\unicode{123}I,-I,\sigma_1,-\sigma_1,i\sigma_2,-i\sigma_2,\sigma_3,-\sigma_3\unicode{125}$, es un Grupo de orden $|G|=8$, cuya magnitud física invariante (con
respecto a la dirección del eje de rotación) de la transformación es
igual a uno.
Conclusión y Transformación Isomorfa $T: P=\unicode{123}I,\sigma_i\unicode{125} \longrightarrow R^{8}$
Finalmente, podemos afirmar que a partir de los tres operadores matriciales de Pauli {$\sigma_x,\sigma_y, \sigma_z$}, se configura el grupo extendido $G$, - (que multiplicado por el factor imaginario $i$), se genera un Algebra de Lie $SU(2)$. Dado que dichas matrices forman una base para $SU(2)$ sobre $R$:
$$
\sigma_x= \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix}
\qquad
\sigma_y= \begin{pmatrix} 0 & -i \\ i & 0 \\ \end{pmatrix}
\qquad
\sigma_z= \begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix}
$$
Desde el punto de vista computacional la incorporación del factor unidad imaginaria $i$, multiplicando los tres operadores de Pauli, se hace más conveniente llevarlo de los Complejos a los Reales, a fin de que los programadores asimilen el concepto de las Algebras de Lie con un nivel de menos abstracción.
Este enfoque de representaciones propio de la Mecánica Cuántica es más próximo a la utilización de la programación de circuitos cuánticos, porque es experimental, no así el enfoque matemático acerca del Algebra de Lie, - que ciertamente-, va poderosamente aun más lejos, pero dentro del algebra abstracta.
De hecho, el espacio vectorial complejo de matrices $2\times 2$, denotado como $M_{2\times 2}(C)$, es isomórfico a $R^{8}$. Es decir, existe un operador $T$ que toma $P=\unicode{123}I,\sigma_i\unicode{125}$ con $i=1,2,3$ y lo lleva a un espacio vectorial real de dimensión 8 (Ver $[B51]$).
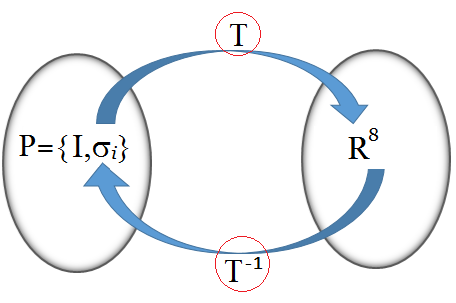
Esta propiedad de isomorfismo implica que $T: P=\unicode{123}I,\sigma_i\unicode{125} \longrightarrow R^{8}$ es biyectiva y lineal, lo que permite transformar bases de un espacio al otro (vice versa) 92.
Es decir, $P=\unicode{123}I,\sigma_i\unicode{125}$ es una base de $M_{2\times 2}(C)$,-(espacio vectorial complejo)-, mapeada por la transformación isomorfa $T$ hacia el espacio vectorial real que se ilustra en la siguiente tabla-matriz:
| $$I$$ |
$$\sigma_1$$ |
$$\sigma_2$$ |
$$\sigma_3$$ |
$$iI$$ |
$$i\sigma_1$$ |
$$i\sigma_2$$ |
$$i\sigma_3$$ |
| $$\downarrow$$ |
$$\downarrow$$ |
$$\downarrow$$ |
$$\downarrow$$ |
$$\downarrow$$ |
$$\downarrow$$ |
$$\downarrow$$ |
$$\downarrow$$ |
| 1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
| 0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
| 0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
| 0 |
0 |
-1 |
0 |
0 |
1 |
0 |
0 |
| 0 |
1 |
0 |
0 |
0 |
0 |
-1 |
0 |
| 0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
| 1 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
| 0 |
0 |
0 |
0 |
1 |
0 |
0 |
-1 |
En síntesis, la tabla muestra que existe un isomorfismo entre la matriz idéntica junto a las matrices Pauli(i.e $\unicode{123}I,\sigma_i\unicode{125}$ ), - desde $M_{2\times 2}(\mathbb{C})$ - , con una base de un espacio vectorial en $R^{8}$ . Esto reafirma que $\unicode{123}I,\sigma_i\unicode{125}$ es una base vectorial en los complejos, dado que es isomorfa con esa base del espacio vectorial real. Los isomorfismos entre bases son vice-versa en términos de propiedades algrebraicas.
Ejemplo Introductorio $\mathbf {z} \in \mathbb C$ ~ Grupo de Lie
Normalización(Ver Complejos Normalizados en Coordenadas Polares)
Se extraen algunos párrafos del documento central Complejos Normalizados en Coordenadas Polares" concernientes a la Normalización de un número complejo, a fin de desarrollar un ejemplo del Grupo de Lie102 en $S(1)$ de rotación pasiva generado por un determinado vector normalizado $ z\in \mathbb C$ en torno al origen $0$.
La idea es mostrar simplemente que el vector $\vec {z_{\theta}}$ cuya norma $|z|=1$, es un operador que al multiplicarlo vectorialmente a otro vector cualquiera en ese plano, lo va a rotar pasivamente en un ángulo $\theta$99.
Cada rotación finita puede descomponerse en un número infinito de rotaciones infinitesimales, ya que el ángulo de rotación puede variar continuamente como $(\alpha + d(\theta)) \quad \text{, donde } d(\theta)\longrightarrow 0$ (Ver Aproximación Fundamental).
$$n \longrightarrow \infty \Rightarrow \frac{\theta}{n} \longrightarrow 0$$
$$\lim\limits_{n\to\infty}\require{cancel}\cancelto{0}{(\frac{\theta}{n})}$$
Desde un punto físico, esto significa como experimentar la rotación de un sólido rígido que resulta del movimiento de uno de sus puntos, manteniendo su posición invariante.

Rotación Pasiva en el Plano $C$
Dicho matemáticamente, se operará bajo el concepto de espacio de Hilbert o espacio euclídeo, con vectores y matrices unitarias, permite ilustrar gráficamente, - normalizar sobre el círculo unitario (conexo) -, un vector $z \in \mathbb C$, también denotado como $\mathbf {z_{\theta}}$ que caracteriza derechamente una transformación de rotación pasiva o Grupo de Lie109.
Por tanto, se comenzará en los complejos con $S(1)\subseteq C^{*}$ (Grupo Discreto), con la restricción $|z|=1$, donde $\unicode{123}x \in R \text{| } x \longrightarrow e^{2\pi i x}\unicode{125}$. Es decir, con el conjunto de unidades complejas que es un Grupo Especial Unitario de Lie (Dim $G =1$) de dimensión uno o grado de libertad del sistema igual $1$, para posteriormente escalar ejemplos en $SO(2), SO(3),\dots $110
Función javascript - Normalización
A continuación, el código de una función en javascript para la normalización de un número complejo $z$, ingresado en forma separada su parte real e imaginaria.
<script language="javascript" type="text/javascript" >
function Normaliza_Complejo(z_real,z_imag) |
|
{ |
z_real=Number(z_real);
z_imag=Number(z_imag);
/* Se valida previamente que z_real y z_img sea números reales */
|
|
|
|
var modulo=Math.pow(z_real,2) + Math.pow(z_imag,2);
|
|
modulo=Math.abs(modulo); |
|
var raiz_modulo=Math.pow(modulo,0.5); |
|
if (raiz_modulo!=0) |
|
{ |
|
var u_real=z_real/raiz_modulo; |
|
var u_imag=z_imag/raiz_modulo; |
|
if (z_imag >=0) |
|
{ |
|
var signo_imag=" + i "; |
|
} |
|
else |
|
{ |
|
var signo_imag=" - i "; |
|
} |
|
} |
|
alert(u_real + signo_imag + Math.abs(u_imag)); |
|
} |
| |
|
///// EJEMPLOS |
|
Normaliza_Complejo(33,-15); |
|
Normaliza_Complejo(-7,13); |
|
Normaliza_Complejo(-3,-8); |
</script> |
Ejemplo Pasos Normalización: $\mathbf {z \longrightarrow e^{i\theta}}$
Un número complejo, $z \in \mathbb C$, tal que $z = x + iy$ también se representa en coordenadas polares como $z = r (cosΘ + i·senΘ)$. Para ese efecto, se establece un plano cartesiano donde el eje de la ordenadas $Y$ se utiliza para el coeficiente del imaginario $\mathit {i}$ y el eje de las abcisas $X$ para el valor de la parte real.
Es decir, inicialmente todo $z \in \mathbb C$ puede expresarse cartesiana y gráficamente como un par ordenado $(x,y)$ sobre el plano y el vector que va desde el origen hasta esas coordenadas lo llamaremos $\overrightarrow r$.
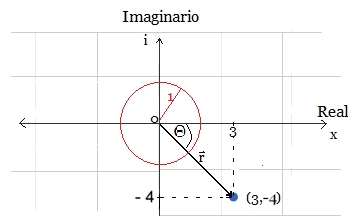
Representación Gráfica de $z = 3 - i·4$
|
Sea $z = 3 - i·4$
$|z|^{2} = x^{2} + y^{2} = 3^{2} + (-4)^{2} = 25$
$|z|=\sqrt{x^{2} + y^{2}}$
$|z| = \sqrt{25} = 5$
$u =\frac{3}{5} - i\frac{4}{5} \Rightarrow |u|^{2}=1$
$tan(\Theta)=\frac {x}{y}$ , donde $x = r·cos(Θ) , y = r·sin(Θ)$
$Θ=tan^{-1}(\frac{x}{y})=tan^{-1}(\frac{-3}{4})=-0.643501109 $
$∴\quadΘ = -0.643501109$
$\Rightarrow Θ=2π- 0.643501109 = 5.63$
$\Rightarrow\quad u = cos(5.63)+ i·sin(5.63)$
$\Rightarrow\quad u = e^{iΘ} = e^{i(5.63)}$
|
Normalizar un número complejo $\mathbf z$ en su forma polar o bajo la fórmula de Euler18, donde se trató $\vec { \mathbf u}$ como la normalización de cualquier vector $\vec {\mathbf z} \in \mathbb C$, de la forma $\mathbf {z= x + iy} \text{ con } \mathbf {x,y} \in R \text{, }\quad \mathbf {i}=\sqrt{-1}$.
Es decir, $\mathbf {\vec u} = e^{iΘ}=cosΘ + i·senΘ$, nos aseguramos que $|u|^{2}=cos^{2}Θ + sen^{2}Θ=1$.
$S(1)$: Grupo de Lie $\iff \vec {\mathbf{ z}} \text{, donde } |z|=1$
En otras palabras, cualquier elemento $\vec {\mathbf{ z}} \in \mathbb C$ normalizado, i.e. cuyo modulo $\mathbf{|z|}=1$, representa un operador para aplicar una rotación pasiva en torno al origen $0$ en el plano. Este operador, cumple la caracterización de Grupo de Lie sobre el cuerpo de los Complejos109.
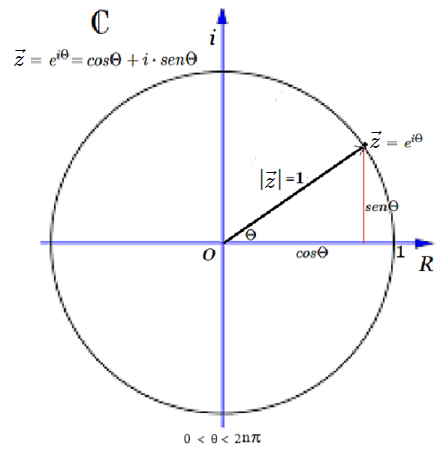
Operador $\mathbf {z_{\theta}}$ ~ Grupo de Lie
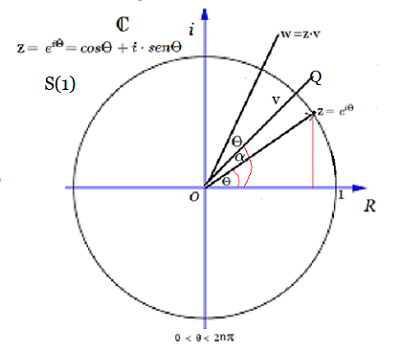
Sea $\mathbf {z_{\theta}}$ el operador lineal que utilizaremos en el ejemplo, el cual lo aplicamos a un vector cualquiera definido en el plano complejo $\mathbf {C}$ de la figura, de la forma $\mathbf {v}=\overline {OQ}$ de ángulo $\alpha$. Es decir,
al multiplicarlo vectorialmente por $\mathbf z$, será rotado en un ángulo $\theta$, obteniendo un vector resultante $\mathbf w$ cuyo ángulo con repecto al eje de la $X$, será de $\theta + \alpha$:
$$ \mathbf {w = z· v} \text{, donde } \mathbf{|w|=|zv|=|v|} \text{, dado que } \mathbf{|z|}=1$$
Sea $v= \mathbf{e}^{i\alpha}\Rightarrow z· w = {e}^{i(\theta + \alpha)}$
Notas Atingentes al Grupo de Lie en $C$
$1$. Producto Interno ~ Espacio Vectorial Complejo
Recordar que el producto interno en un espacio vectorial complejo, se define de manera diferente al producto interno en los Reales. En efecto,
Sea $V$ un espacio vectorial complejo. Una función $ \mathfrak g: V × V \longrightarrow V \in \mathbb C$ se denomina producto interno en
$V$, si cumple con las siguientes propiedades:
$ii)\quad \mathfrak g$ es lineal con respecto al segundo argumento:
$$\mathfrak g(u, v + w) = \mathfrak g(u, v) + \mathfrak g(u, w) \qquad \forall u, v, w \in V $$
$$\mathfrak g(u, \lambda v) = \lambda \mathfrak g(u, v)\qquad \forall u, v \in V \qquad \forall \lambda v \in \mathbb C$$
$ ii)\quad \mathfrak g$ es hermítica($g^{†}=(g^{T})^{*})$:
$$\mathfrak g(u, v) = \overline{\mathfrak g(v, u)} \qquad \forall u,v \in V$$
$iii)\quad \mathfrak g$ es definida positiva:
$$\mathfrak g(v, v) \gt 0 \qquad \forall v \in V \text{ \ }\unicode{123}0 \unicode{125}$$.
$2$. $(C^{*},·)$: El Grupo Multiplicativo de los Complejos Diferente de Cero
Dado que se hace mención al grupos discretos $C^{*}$, a continuación se establecen y descripción del grupo multiplicativo de los números complejos diferente de cero.
Aparte de la definición de grupo80, equivalentemente se pueden postular con los siguientes puntos para constituir un grupo:
i) Se define un conjunto $S \ne \phi$
ii) Se define una operación binaria $·$ en $S$
iii) Se verifica que $(S,·)$ tiene un elemento neutro
iv) Se verifica que $(S,·)$ es un semigrupo, i.e. que es asociativo
v) Se verifica que todo elemento de $S$ tiene un inverso.
A continuación, se verifica con cada uno de estos puntos previamente especificados que $C^*$, es un grupo multiplicativo de los números complejos diferente de cero.
- i) Sea $C^*$ el conjunto de los números complejos diferente de cero:
$$C^{*}=\unicode{123} z \in \mathbb C \text{ | } z = a + ib \text{, donde } z \ne (0 + i·0)\quad \land \quad a,b \in R \unicode{125}\qquad \color{red}{✓}$$
Recuérdese que $i^2=-1$
- ii) Se reitera la definición de la multiplicación de números complejos, los cuales es posible multiplicarlos como si fueran polinomios. Donde $(a,b,c,d,e,f \in R \quad \land \quad i=\sqrt{-1})\qquad \color{red}{✓}$
$$(a + i· b)(c +i· d)=ac + i^2 · bd + i· ad + i· bc (ac-bd) + i·(ad+c) \qquad \color{red}{✓}$$
Esta operación binaria se da en $C^{*}$, porque su resultante $(ac-bd)+i(ad+c)$ es un elemento único en $C^{*}$. Es decir, no pueden ser simultáneamente iguales a cero.
- iii) $1 + i·0 = 1 \in \mathbb C^{*}$ y es evidente que $1$ es el neutro multiplicativo de $(C^{*},·)\qquad \color{red}{✓}$
- iv) Consideremos tres números $(a + i·b),(c + i·d),(e + i·f) \in \mathbb C^{*}$. Entonces:
|
$$(a + i·b)(c + i·d)(e+ i·f)=[(ac - bd)+i·(bc + ad)](e + i·f)$$ |
| |
| $$=[(ac-bd)e-(bc+ad)f)] + i·[bc+ad)e+(ac-bd)f] \qquad \color{red}{✓}$$ |
Por otra parte,
$$(a + i·b)[(c + i·d)(e + i·f)]=(a + i·b)[(ce-df) + i·(de + cf)]$$
$$=a(cd-ef)-b(de+cf) + i·[b(ce-df) + a(dc+cf)]$$
Luego, esta igualdad implica:
|
|
$$(a + i·b)[(c + i·d)(e + i·f)]=[(a + i·b)(c + i·d)]+(e + i·f)\qquad \color{red}{✓}$$
|
- v) Ahora, se comprobará la existencia de los inversos. Considérese $z = (a + i· b) \in \mathbb C^{*}$.
Entonces $a \ne 0 \text{ y } b \ne 0 $, i.e. $a \text{ y } b$ no son simultáneamente cero. Esto implica que $(a^{2}+b^{2})\ne 0$ y por tanto:
$$\frac{a}{(a^{2}+b^{2})} + i\frac{b}{(a^{2}+b^{2})} \in \mathbb C^{*}\qquad \color{red}{✓}$$
Más aún:
$$\Bigl(\frac{a}{(a^{2}+b^{2})} - i\frac{b}{(a^{2}+b^{2})}\Bigr)(a + i·b)=1=(a + i·b)\Bigl(\frac{a}{(a^{2}+b^{2})} - i\frac{b}{(a^{2}+b^{2})}\Bigr) \qquad \color{red}{✓}$$
En otras palabras, todo número complejo $z=a + i·b$ no nulo tiene un inverso multiplicativo. Es decir, existe $z^{-1}$ tal que $z^{-1}z=zz^{-1}=1$
$$
\begin{equation*}
z^{-1} = \frac{a-i·b}{ a^2 + b^2 }.
\end{equation*}
$$
En la normalización de un número complejo $z=a + i·b$, se demostró que al multiplicar por su conjugado, definido como $\overline {z}=(a - i·b)$ , resulta $|z|^2=z·\overline {z} = a^2+b^2 \Rightarrow |z|=1$.
De esta forma se ha demostrado que $C^{*}$ es un grupo, el cual es denominado Grupo Multiplicativo de los Números Complejos Diferente de Cero.
|
Continuación$\longrightarrow$
Ver artículo complementario Grupo de Lie - Enfoques Geométrico y Exponencial 
Ver Video: Grupo de Lie ~ Complementario a Matrices de Pauli y Algebra de Lie 
|
|






