

| + Ficha Técnica |
|
Ejercicio Robot Móvil
José Enrique González Cornejo
|
|
Introducción El presente artículo ilustra mediante un ejemplo un planteamiento simple y práctico, cómo combinar los enfoques de la ruta óptima por tramos y el uso de un modelo bayesiano (Naïve Bayes 1) que permite robustecer un algoritmo de modelamiento y aprendizaje automático de un robot móvil. El documento muestra un procedimiento mixto de dos enfoques para intentar alcanzar un sistema óptimo de búsqueda de rutas en un determinado espacio $S$, cuyos subespacios $\large{s_i}$ se representan como un punto de un grafo $G$. Esto, a fin de operar en situaciones complicadas y dinámicas incluídas en el Sistema de Información del mapeo inicial. Se reitera que la clave del Algorimo de Dijkstra es que en cada punto o nodo se usan sólo dos lineas: una para ingresar y otra para salir del punto. Es decir, cada nodo será explorado sólo una vez en su visita. Desde ahí, se utiliza una de sus líneas salientes de acuerdo a las métrica más corta (distancia, costo, tiempo,.. ) para visitae el siguiente nodo. Esta presentación es un complemento anexo del artículo Ruta Optima por Tramos  , con dos publicaciones adjuntas, por una parte una aplicación computacional de Simulación Aleatoria de Algoritmo , con dos publicaciones adjuntas, por una parte una aplicación computacional de Simulación Aleatoria de Algoritmo  , y por otra un video Algoritmo para la Ruta Optima por Tramos , y por otra un video Algoritmo para la Ruta Optima por Tramos  . .
Junto a estas dos publicaciones directamente relacionadas, se realizan múltiples referencias bibliográficas a conceptos desarrollados en los siguientes videos:
Robot Móvil Supongamos se programa un robot móvil terrestre 2 para recorrer un espacio $S$ determinado, comenzando en un punto de origen hasta un punto de destino. Para ese efecto, se aplicarán cálculos utilizando y confrontando las resultantes de dos enfoques algorítmicos:
ii) Verificando mediante Teorema de Bayes el entorno donde se encuentra, i.e. su localización actual para predecir su próxima ubicación. 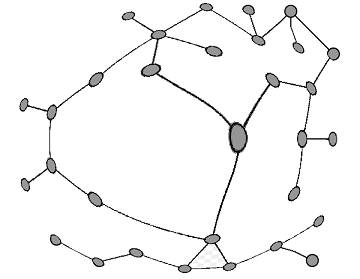 Espacio $S$ sintetizado en un grafo $G$ Basándose en estos dos pilares del algoritmo, el robot toma decisiones sobre su siguiente movimiento y acciones, como evitar obstáculos, seguir una ruta planificada o buscar un objetivo. Esta combinación de enfoques es particularmente útil en entornos dinámicos, donde las condiciones pueden cambiar y donde la precisión de la localización es crucial para la seguridad y eficiencia del robot. Es claro que, la clave del algoritmo es tener la capacidad de planificar el camino a seguir para llegar desde un punto de inicio a un punto de destino evitando obstáculos y siguiendo una ruta eficiente. Desde el algoritmo de la Ruta Optima por Tramos se obtiene una visión global e inicial de la ruta de navegación ponderada 3, por otra parte, el reconocimiento del espacio que ejecuta el robot, para determinar dónde está situado (objetos) 4 y de dónde viene, se complementa la decisión para elegir la línea de salida mediante la probabilidad bayesiana. Es decir, la combinación de estos dos enfoques permite al robot tomar decisiones más informadas sobre su movimiento, considerando tanto la planificación de ruta óptima como la mejora continua de su estimación de posición en tiempo real. De modo que el robot se mueve y toma nuevas mediciones, el proceso se repite en cada punto durante cada iteración, ajustándose para reflejar con mayor precisión su ubicación en el entorno y obtener un método que genere caminos sin mayores obstáculos. Una ventaja del uso del Teorema de Bayes en este caso, es que el robot tiene información inicial de dónde está ubicado y de dónde viene. Nótese de que otra forma,- i.e. sin un grafo predeterminado -, la programación de un robot autónomo es mucho más compleja. Efectivamente, es una ventaja contar con una "ruta óptima" inicial. Luego, para reforzar el contexto de la navegación y percepción de objetos en un entorno se requiere alimentar con datos y casos de uso en la supervisión del robot (Learning Machine) 5 Es necesario recordar que las estimaciones bayesianas no sólo se basan en las frecuencias estadísticas de las evidencias empíricas, sino que también admiten el conocimiento de expertos, casos de uso, y conocimiento a priori, el cual se incorpora a las bases del cálculo y decisiones que va ir tomando el robot. (Ver Experimento ~ Supervisión y Entrenamiento ~ Inteligencia Artificial ~ Naïve Bayes Learning Machine) Síntesis Combinación Enfoques En síntesis, la combinación de estos dos enfoques en el algoritmo del robot es:
ii) Se utiliza el algoritmo de la ruta óptima para encontrar el camino inicial más corto desde el punto de inicio $\large{p_1}$ hasta el punto de destino $\large p_n$ sobre el grafo $G$, considerando las distancias y posiblemente la dificultad para atravesar ciertas áreas (como obstáculos). iii) El robot utiliza sus sensores 11 para obtener mediciones de su entorno y estimar su posición actual. iv) Se aplica el Teorema de Bayes para actualizar la coordenadas y data clasificatoria del robot acerca de su posición, en función de las mediciones de los sensores y la información previa sobre su posición. v) El camino inicial planificado por el algoritmo puede ser modificado de acuerdo la información de la localización actualizada mediante la estimación probabilística del Teorema de Bayes. vi) Un ajuste puede significar que el robot modifica completamente el paso por los puntos de la ruta previa, con el fin de evitar obstáculos detectados y adaptarse un nuevo rumbo hacia su punto objetivo $\large {p_n}$. Notación de Grafos Utilizada Dentro del espacio $S$, podría tratarse con obstáculos estáticos o dinámicos. El algoritmo de navegación de este ejemplo es dinámico, pero mapeado con una ruta generada inicialmente con la solución de Dijkstra, y la adaptación de las situaciones cambiantes se abordará con la probabilidad bayesiana ya aprendida o por aprender del robot.
Se entiende que una ruta de un grafo $G$ es una secuencia conexa de alternancia de puntos y líneas: $$\unicode{123}\large{p_0, q_1, p1, q_2, p2, q3, p3,\dots q_n, p_n}\unicode{125}$$ Ruta que comienza y termina en puntos, donde cada línea incide con dos puntos. El punto que le precede y el siguiente punto. También es posible representar las relaciones entre los puntos de una grafo $G$ con la Matriz de Adyacencia $A=\large{[a_{ij}]}$ de $\large{n}$ puntos. $A=\large{[a_{ij}]}$ es una matriz $\large{n\times n}$, donde a $\large{a_{ij}=1}$ si $\large{p_i}$ es adyacente con $\large{p_j}$ y $\large{a_{ij}=0}$ si es de otra forma. Por ejemplo: 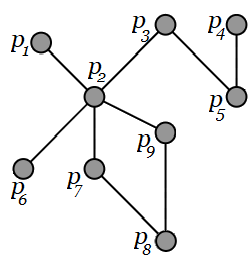
Grafo $G_{A}$
La Suma de una fila ($\large{p_{i}}$) o columna $\large{p_{j}}$, resulta ser el número de líneas que incide en el punto, i.e. el grado del nodo. 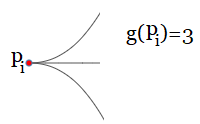 Grado $\large{g({p_i})=3}$, N°de Líneas que inciden en $\large{p_i}$ Nótese, que el grado de un punto en un grafo es el número de líneas que inciden en él. Es decir, el grado de un punto $\large{p_i}$ se denota como: $$\large{g(p_{i})=k, \quad \text{,donde }k\in \mathbb N\cup\unicode{123}0\unicode{125}}$$ 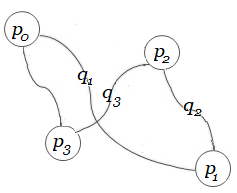 $\large{{p_0} \frac{\quad q_1 \quad}{}{p_1} \frac{\quad q_2 \quad}{} {p_2} \frac{\quad q_3 \quad}{}p_3}$ Los puntos son rotulados por $\large{p_i}$, las líneas por $\large{q_{ij}}$ y los valores o ponderaciones de las líneas se denotan por $\large{m_{ij}}$, i.e. como los elementos de la matriz adjunta a grafo $\large{M_{n\times n}}$. En otros términos, el valor $\large{v(q_{ij})= m_{ij}}$, donde $\large{m_{ij} \in \mathbb R}$, i.e. $\large{p_i}$ es el nodo de orijen y $\large{p_j}$ el nodo de destino. (Si la ruta del grafo, vuelve a su punto inicial se dice que es una ruta o camino cerrado o es un ciclo.) Por tanto, el algoritmo que se describe en el presente artículo cuenta con un parámetro $\large {p}$ que es el número de puntos y $\large {q =(p-1)}$ que es el número de líneas, donde los ejercicios que utilizaré son $\large {p=n, n\gt 2, n \in \mathbb {N}}$ i.e. internamente se genera un grafo completo $G$ con su matriz adjunta $\large{M_{n\times n}}$.
$\large{p}$: Número total de puntos de $\large{G}$; $\large{q}$: Número total de líneas de $\large{G}$; $\large{p_i}$: Rótulo de un punto del grafo; $\large {q_{ij}}$: Rótulo de línea que incide en el punto $p_i$; $\large {g(p_i)}$: Grado o número de líneas que inciden en $p_i$ $\large{s_{i}\mapsto p_{i}}$: Subespacio de $\large{S}$ compuesto por objetos $\large{o_{ij}}$ y representado por $\large{p_{i}}\in G$ $\large{o_{ij}}$: Objetos registrados y localizados en el espacio representado por $\large{p_i}$, con $\large{j=1,2,3,\dots ,m}$ $\large {m_{ij}}$: Valor o ponderación, - o también denotado por la métrica $\large{d(i,j)}$ -, asignado a la conexión entre $\large{p_i}$ con $\large{p_j}$ o $\large{v(q_i)=m_{ij}}$. (En general, $\large{m_{ij}\in \mathbb R}$) $\large {M_{n\times n}}$: Matriz Cuadrada Adjunta a $\large{G}$, donde $\large{n}$ el número de nodos o puntos. Se asume que el entorno en el que opera el robot se puede representar como un espacio discreto, donde cada celda de la matriz adjunta o nodo representa una posible ubicación y estado verificado del robot dado los objetos detectables a su alrededor. (Para la programación de un robot en un espacio continuo, ver Algebra de Lie - Aplicaciones ~ Formalización). Estimación Bayesiana Aplicar estimaciones bayesianas presupone que el robot está equipado con sensores (cámaras, ultrasonido, GPS u otros dispositivos de detección) que le permiten percibir su entorno.  Robot Terrestre - Sensores - Base Datos - Nube En efecto, en función de esa data preestablecida -, conectada al robot desde una base de datos-, es posible aplicar el teorema de Bayes, específicamente en el contexto de la navegación y percepción de objetos en un entorno y distribución de probabilidad sobre las ubicaciones posibles. Se estiman las probabilidades predictivas, dentro de un entorno Bayesiano, sea con distribuciones discretas como continuas (Gauss o Bernoulli). Entonces, un entorno Bayesiano es un modelo probabilístico que contiene algún tipo de conocimiento previo, acerca de un parámetro investigativo. De este modo con la data empírica se constituye la configuración del conocimiento del modelo 7.
Ejemplo de Estimación Bayesiana El siguiente diagrama muestra un espacio $\large{s_i}$, que contiene tres objetos registrados {$\large {o_{i1},o_{i2},o_{i3}}$} en la data de reconocimiento del robot. Luego $\large{p_i}$ es el lugar, donde ingresó en robot que explorará y verificará si es el punto planificado y elegirá una de las dos salidas para continuar su navegación 8. $$\large{s_{i}\mapsto p_{i}}$$ 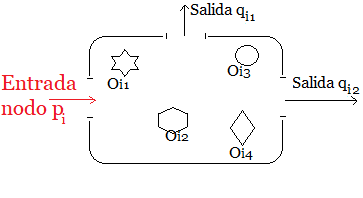
Espacio con 3 Objetos Registrados y 2 Salidas El siguiente grafo sintetiza el espacio a verificar con la línea de ingreso en rojo y las dos líneas de salidas con la notación {$q_{i1},q_{i2}$}. 
Punto $p_i$ que Representa Espacio y sus Dos Líneas de Salida $q_{ij}$ Supongamos que el robot ingresó en un punto $\large p_i$ y debe llegar al punto $\large p_n$. Para continuar la ruta desde $\large p_i$, se ofrecen dos salidas:
ii) La salida por la línea $\large {q_{i2}}$. A partir de esa información, se definen los eventos con las condiciones de tráfico a evaluar:
- El evento por la salida $\large{q_{i2}}$ que pasa que por el punto $\large{p_b}$ para llegar a $\large{p_n}$. Es decir, $$\large{p_i\longrightarrow p_a \longrightarrow p_n}\\ \lor \\ \large{p_i\longrightarrow p_b \longrightarrow p_n}$$ A ambos eventos se les asigna una probabilidad "a priori" asociada a la facilidad de transito (i.e. mayor probabilidad es mejor): $$\large{p_1\overset{\large{\frac{3}{5}}}{\longrightarrow} p_a \overset{\large{\frac{3}{8}}} \longrightarrow p_n}$$ $$\lor$$ $$\large{p_1\overset{\large{\frac{2}{5}}}{\longrightarrow} p_b \overset{\large{\frac{1}{2}}} \longrightarrow p_n}$$ Las probabilidades estimadas basadas en datos en tiempo real de ese instante, se ilustran en el diagrama de árbol: 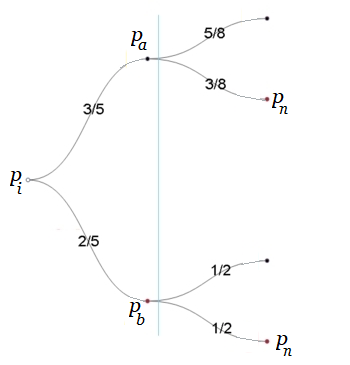
Diagrama: Opciones de Salida y Llegada a $p_n$ 10 Luego, cabe preguntar:
- ¿Cúal es la probabilidad de llegar a $\large {p_n}$, si su salida desde $\large {p_i}$ fue por la ruta $\large {q_{i2}}$? - ¿Cuál de las dos rutas es más conveniente? $$\large{\underbrace{P(p_n)}_{Probabilidad \text{ }Total}=\underbrace{P(p_n|p_a)P(p_a)}_{p_a\land p_n}}$$ $$\underbrace{+}_{\lor}$$ $$\underbrace{P(p_n|p_b)P(p_b)}_{p_b\land p_n}$$ $$ \large{P(p_n)=\underbrace{\frac{3}{5}}_{P(p_a)}·\underbrace{\frac{3}{8}}_{P(p_n)} + \underbrace{\frac{2}{5}}_{P(p_b)}·\underbrace{\frac{1}{2}}_{P(p_n)}}$$ $$ \large{\underbrace{P(p_n)}_{Probabilidad \text{ }Total}=0.425}$$ Ahora calculemos las probabilidades condicionales de llegar a $\large {p_n}$ de cada una de las opciones (i.e. el numerador de la expresión $[1]$): $$\large{P(p_n|p_a)P(p_a)=\frac{3}{5}·\frac{3}{8}=\frac{9}{40}}$$ $$\large{P(p_n|p_b)P(p_b)=\frac{2}{5}·\frac{1}{2}=\frac{1}{5}}$$ De donde de obtiene la siguiente desigualdad, $$\large{\frac{9}{40} \gt \frac{1}{5} \iff 0.225 \gt 0.2}$$ Nótese, que la probabilidad de cada una de las rutas con la formulación de Bayes es la siguiente: $$\large{\require{cancel} \frac{P(p_n|p_a)P(p_a)}{\cancel{P(p_n)}}\gt \frac{P(p_n|p_b)P(p_b)}{\cancel{P(p_n)}}}$$ $$\large{\require{cancel} \frac{0.225} {\cancel{0.425}} \gt \frac{0.2}{\cancel{0.425}}}$$ Por lo tanto, el robot elige la salida $\large{q_{i1}}$ pasa por el punto $\large{p_a}$ para llegar a $\large{p_n}$ 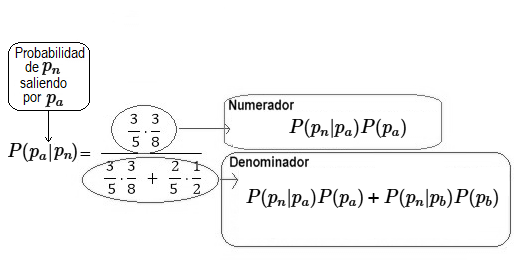 Probabilidad de ir al destino $\large{p_n}$ por $\large{p_a}$ $$\large{p_i\longrightarrow p_a \longrightarrow p_n}$$ (Ver video Naïve Bayes ~ Simple Algoritmo de Clasificación Modelo de Variables Discretas). Cambio de Ruta El ejemplo de Grafo Completo de 6 Puntos con nodos rotulados con las letras {$A,B,C,D,E,F$}, donde el algoritmo de la "ruta óptima por tramos", entregó inicialmente el camino hamiltoniano 9 óptimo y cerrado $$A\longrightarrow F \longrightarrow D \longrightarrow E\longrightarrow C \longrightarrow B \longrightarrow A$$ Luego, supongamos que cuando el robot ingresa en el punto $F$, recibe información que señala que el camino hacia su próximo destino programado $D$, - cuya ponderación es de $1$ - , tiene un incidente que podría aumentar su valor a $5$. Ahí, el algoritmo inmediatamente verifica las otras $4$ líneas de salida que inciden en dicho punto y analiza el cambio de la ruta, i.e. elige un nuevo sub-camino halmitoniano óptimo que lo llevará de vuelta al punto $A$. El nuevo camino debe ser, - en lo posible-, cercano al camino planificado. 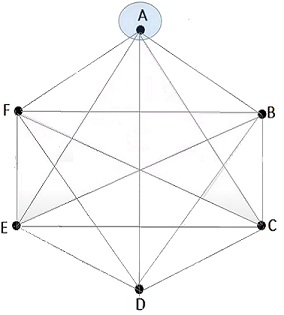 Grafo Completo de 6 puntos 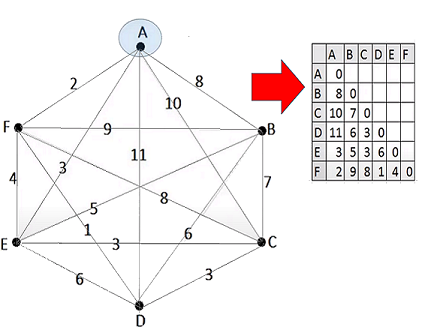 Grafo de 6 puntos ~ Matriz Adjunta con Valores por línea El trayecto que hará el robot será desde un punto de inicio $\large {p_1}$ hasta un punto de destino $\large {p_n}$, a través de un camino hamiltoniano, y con la capacidad de utilizar cálculos e ir actualizando la probabilidad de cuál es su ubicación, dado el conocimiento previo y la información sensorial actual. 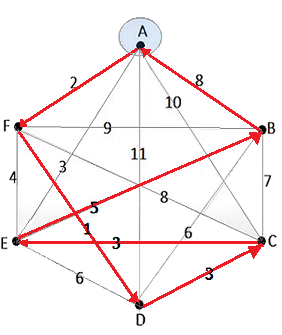 $A \overset{2}{\longmapsto} F \overset{1}{\longrightarrow} D \overset{3}{\longrightarrow}E \overset{3}{\longrightarrow}C \overset{5}{\longrightarrow}B \overset{8}{\longrightarrow}A$ El algoritmo con las la instrucción de los nodos de inicio y destino, $\large {p_1 \longrightarrow p_n}$, i.e. ya tiene identificado su posición de inicio y el destino u objetivo a alcanzar. Ahí la regla de Bayes es una parte fundamental para la estimación de la posición, reconocimiento y la toma de decisiones del robot móvil descrito. 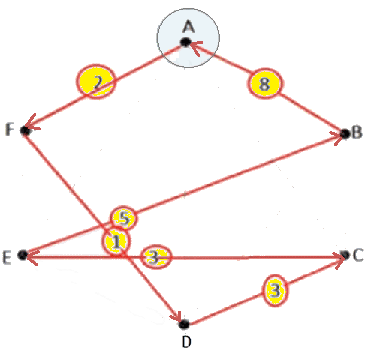 Ruta Optima Inicial Calculada $$\sum Min(d_{ij})=22$$ El robot debe evitar obstáculos, así mismo está supervisado para reconocer ciertos objetos $\large {o_{ij}}$ ya registrados respectivamente que contienen los subespacios que son tratados como puntos o nodos del grafo $G$. Cada subespacio o nodo $\large p_i$, cuenta con un conjunto de objetos $\large {o_{ij}}$, donde $i=1,2,3,\dots n \land j=1,2,3,\dots m$ registrados que van a garantizar cierta adaptabilidad con respecto a los diferentes tipos de obstáculos y terreno, puesto que el robot puede triangular el espacio $\large {p_i}$ y detectar sus objetos asociados $\large {o_{ij}}$ Luego, el algoritmo de la ruta óptima por tramos planifica su trayecto inicial calculando la ruta más corta y segura entre dos puntos en un entorno tridimensional o bidimensional y por otra parte recibe soporte de verificación por parte del Teorema de Bayes (Ver ¿Cómo Entender el Teorema de Bayes en Forma Simple?  ). ).
Conclusión El robot entonces, estima inicialmente el entorno en el que operará con el grafo $G$, donde los nodos $\large {p_i}$ representa las ubicaciones en el espacio y las líneas $\large {q_{ij}}$ representan las conexiones posibles entre esas localizaciones. Así mismo, las mediciones bayesianas se utilizan para calcular la probabilidad de que el robot esté en una ubicación dada en función de las observaciones actuales. Es decir, las restricciones o verificación del trayecto será mediante el reconocimiento de objetos del lugar, de acuerdo a lectura de los sensores, para percibir y/o detectar objetos u información relevante, como obstáculos. Cada línea tiene un valor asignado de acuerdo a la métrica definida, donde en este caso se usará sea la distancia o el costo de desplazarse entre los puntos. Dado que el algoritmo de la ruta óptima por tramos se aplica al grafo del entorno, calculando las distancias más cortas desde $p_1$ a todos los demás nodos del grafo y que, durante este proceso, se consideran los valores de las líneas para determinar la ruta más corta o barata. La seguridad de estar en el subespacio $\large {s_{i} \mapsto p_{i}}$ el algoritmo lo ayudará a garantizar el entorno donde está ubicado y el próximo paso de su camino hamiltoniano. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Canal Youtube Notas Adjuntas |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Artículos Relacionados | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| DocIRS © 1988 - 2026 |