
|
|

Modelo Clasificación de Crédito a Potenciales Clientes |
|
Introducción
"Naïve Bayes o Bayes Ingenuo" es un instrumento estadístico, cuya variable a explicar es generalmente dicotómica, se utiliza en Minería de Datos e Inteligencia Artificial (Learning Machine), guardando cierta analogía con la la distribución estadística Logit, dado que ambos métodos se basan en la frecuencia relativa de variables categóricas o clases o atributos, a fin de obtener información relevante para el análisis de toma de decisiones en base a predicciones probabilísticas.
En efecto, la Logit es una regresión que predice el resultado de una variable categórica en función de las variables 'independientes' o explicativas predictoras. La Logit, - obviamente como todas las distribuciones estadísticas-, no predice determinísticamente $0$ ó $1$, sino que la regresión logística genera una probabilidad con un valor entre $0$ ó $1$.
En resumen, se muestra cómo se aplicará la estimación de la Logit, cómo se obtienen los parámetros básicos. La regresión lineal utilizada obviamente puede ser múltiple. Sin embargo, aquí se utiliza una sola variable independiente que intenta explicar la variación de la variable dicotómica (o "dummy"). También se utiliza un ejemplo que ilustra el procedimiento como se agrega la data, y se realiza el procedimeinto con los cálculos.
El modelo Logit

Representación Gráfica de Función Logit2
El modelo Logit, se define a partir de la siguiente función de distribución:
y las variables se definen de la siguiente forma: |
|
|
Linearización: Transformación Logarítmica
|
Ejemplo de Clasificación
La idea central del ejemplo es ilustrar el método, levantando datos propios y clasificar basado en comportamientos o características de datos de clientes almacenados.
El objetivo es realizar predicciones en función de patrones históricos de grupos de clientes. En este caso, se trabajará con la variable ingreso sobre una pequeña muestra de observaciones. Obviamente, una función de una sóla variable o atributo es insuficiente para armar un criterio de evaluación consistente.
No obstante, comprender el procedimiento de este instrumento estadístico Logit señalará aun mejor la diferencia con el método "Learning Machine~ Naïve Bayes o Bayes Ingenuo", especialmente en lo referente al mayor número de variables o atributos (que se asumen mutuamente excluyentes), - que pueden explicar la variable dependiente-, incluidos en el modelo. Este hecho, facilita el tratamiento estadístico de datos, y también en sacar conclusiones válidas para tomar decisiones en base a ese análisis.(Ver Algoritmo Naïve Bayes Explicado con Tablas Dinámicas Excel)
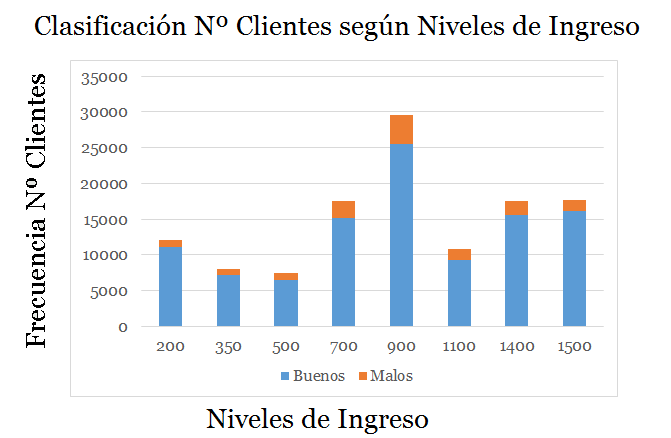
Muestra de Datos
Se ha extraído una muestra de 120.800 de observaciones de clientes de la base datos. Filtrando por cada cliente su ingreso expresado en una unidad monetaria y su cumplimiento de pago respectivo.
La muestra se ha distribuido en 9 clases o intervalos de ingresos, asociando la frecuencia a la variable dicotómica si cumplió o no cumplió.
| Clase | Intervalo Ingreso |
|---|---|
| 1 | $$0\lt X_1 \leq 200$$ |
| 2 | $$200\lt X_2 \leq 350$$ |
| 3 | $$350\lt X_3 \leq 500$$ |
| 4 | $$500\lt X_4 \leq 700$$ |
| 5 | $$700\lt X_5 \leq 900$$ |
| 6 | $$900\lt X_6 \leq 1100$$ |
| 7 | $$1100\lt X_7 \leq 1300$$ |
| 8 | $$1400\lt X_8 \leq 1500$$ |
| 9 | $$X_9 \gt 1500$$ |
A continuación se ilustra la configuración del diagrama de árbol:

| Ingreso en Miles de $ | Cumplió | No_Cumplió | Tamaño Clase |
|---|---|---|---|
| $$X_i$$ | $$n_{1i}$$ | $$n_{2i}$$ | $$N_{i}$$ |
| 200 | 11078 | 1022 | 12100 |
| 350 | 7147 | 853 | 8000 |
| 500 | 6539 | 861 | 7400 |
| 700 | 15224 | 2376 | 17600 |
| 900 | 25521 | 4079 | 29600 |
| 1100 | 9342 | 1458 | 10800 |
| 1400 | 15564 | 2036 | 17600 |
| 1500 | 16164 | 1536 | 17700 |
| 1850 | 9819 | 881 | 10700 |
| Total | 106579 | 14221 | 120800 |
|
Tal como lo muestra la Tabla $1$ para cada nivel de
ingreso $X_i$, existen $N_i$ clientes. Donde $n_{1i}$
representa el número de créditos "Cumplió" y $n_{2i}$
los "No_Cumplió" para cada nivel de ingreso $X_i$, $N_i$
representa el tamaño del intervalo respectivo. Es decir; $N_i = n_{1i} + n_{2i}$.
|
|
Estimación Parámetros
|
| Utilizando la Tabla $1$ y aplicando las expresiones $[4]$ y $[3]$ se obtiene la siguiente tabla: |
| Ingresos | Si Pagan |
No Pagan |
Tamaño Clase |
Prob. Cumplió |
Prob. No_Cumplió |
Razón | Logit Li |
|---|---|---|---|---|---|---|---|
| $X_i$ | $n_{1i}$ | $n_{2i}$ | $N_i$ | $\hat{P_i}$ | $1-\hat{P_i}$ | $\frac{\hat{P_i}}{(1-\hat{P_i})}$ | $Ln(\frac{\hat P_i}{(1-\hat P_i)})$ |
| 200 | 11078 | 1022 | 12100 | 0,9155 | 0,0845 | 10,8343 | 2,3827 |
| 350 | 7147 | 853 | 8000 | 0,8934 | 0,1066 | 8,3809 | 2,1260 |
| 500 | 6539 | 861 | 7400 | 0,8837 | 0,1163 | 7,5985 | 2,0279 |
| 700 | 15224 | 2376 | 17600 | 0,8650 | 0,1350 | 6,4074 | 1,8575 |
| 900 | 25521 | 4079 | 29600 | 0,8622 | 0,1378 | 6,2569 | 1,8337 |
| 1100 | 9342 | 1458 | 10800 | 0,8650 | 0,1350 | 6,4074 | 1,8575 |
| 1400 | 15564 | 2036 | 17600 | 0,8843 | 0,1157 | 7,6430 | 2,0338 |
| 1500 | 16164 | 1536 | 17700 | 0,9132 | 0,0868 | 10,5207 | 2,3533 |
| 1850 | 9819 | 881 | 10700 | 0,9177 | 0,0823 | 11,1507 | 2,4115 |
| Total | 106579 | 14221 | 120800 | - | - | - | - |
|
Aplicando el Método de los Mínimos Cuadrados y regresando las cifras de acuerdo a la expresión $[2]$ , entonces la variable dependiente $L_i$ explicada por $X_i$ arroja los siguientes parámetros estimados: |
| Parámetro Estimado | Valor |
|---|---|
| $\hat{\beta_0}$ | 2,011432424 |
| $\hat{\beta_1}$ | 9,18776E-05 |
| $R^{2}$ | 0,048491063 |
Cálculo del Error
| $X_i$ | $L_i$ | $\hat {L_i}$ | $\mu$ | $\mu^{2}$ |
|---|---|---|---|---|
| 200 | 2,38271883 | 2,0298 | 0,3529 | 0,1245 |
| 350 | 2,1259509 | 2,0436 | 0,0824 | 0,0068 |
| 500 | 2,02794458 | 2,0574 | -0,0294 | 0,0009 |
| 700 | 1,85745473 | 2,0757 | -0,2183 | 0,0477 |
| 900 | 1,8336839 | 2,0941 | -0,2604 | 0,0678 |
| 1100 | 1,85745473 | 2,1125 | -0,2550 | 0,0650 |
| 1400 | 2,03379574 | 2,1401 | -0,1063 | 0,0113 |
| 1500 | 2,35334829 | 2,1492 | 0,2041 | 0,0417 |
| 1850 | 2,41149943 | 2,1814 | 0,2301 | 0,0529 |
| $\sum u^{2}$ | 0,4186 |
Estimación e Interpretación
| Modelo Propuesto | Modelo Estimado | |
|---|---|---|
| $$L_i=\biggl(\frac{P_i}{(1-P_i)}\biggr)=\beta_0 + \beta_1 X_1$$ | $$\longrightarrow$$ | $$\hat L_i=\biggl(\frac{\hat P_i}{(1-\hat P_i)}\biggr)=\hat \beta_0 + \hat \beta_1 X_1 + \hat \mu $$ |
En este caso, se usa la regresión logística en una variable, correlacionando la probabilidad binaria del cumplimiento de pago de un crédito utilizando los valores $\unicode{123}0,1\unicode{125}$, explicados por una variable escalar categorizada que es el ingreso. Si la aplicación de la Logit arroja la probabilidad de obtener $0$ el evento es "No_Cumplió" y si aproxima $1$ el evento es "Cumplió".
En el modelo Logit propuesto se asume que existen valores ideales que representan perfectamente el cálculo y predicción (coeficientes sin ^). Dicho modelo, el cual se aproxima mediante la muestra de datos en el modelo Logit estimado. Es decir, los estimadores (con ^) $\unicode{123}\hat\beta_0, \hat \beta_1, \hat\mu \unicode{125}$ obtenidos del procesamiento de los datos intentan ajustarse a la curva supuestamente perfecta, mediante el método de los mínimos cuadrados.
La interpretación del modelo Logit señala que el coeficiente $\beta_1$ es la pendiente que mide la variación de $L$
cuando ocurre un cambio de una unidad en el ingreso. Aquí se puede utilizar el concepto de elasticidad5, que
es la variación porcentual que experimenta una variable dependiente en respuesta a la
variación porcentual de una variable explicativa.
El cambio, lógicamente se puede calcular derivando simplemente $L_i$ con respecto a $\hat X_1$, dado que tanto $X_0$ como $\mu$ son constantes. En caso de incluir más variables explicativas en el modelo se debe derivar parcialmente. En este caso la tasa de cambio es:
$$\frac{d L}{d \hat X_1}=\beta_1$$
El intercepto $\beta_0$ es el valor inicial del ingreso. Cuando el valor constante del intercepto es igual a $0$ indica que la curva pasa por el origen. La interpretación física del intercepto,- en general -, no tiene mayor significado. Excepto cuando esté dada como condición de borde en un enunciado.
El valor del error o residuo o perturbación $\mu$, se incluye como la parte inexplicada del modelo interpretado por diversas influencias aleatorias sobre el diseño y su medición. Errores que se producen a causa de variables omitidas, variables no observables, errores de medición, errores de especificación y particularmente por los hipotéticos supuestos de base de linealidad del método.
El análisis del error es complejo y de gran importancia en la medición de modelos lineales. Recordar que los estimadores se trabajan bajo desviaciones con respecto a la media. (Ver Deducción)
En este caso los tratamos en forma simple y coloquial, donde el valor estimado de $\hat \mu$ contribuye a "cuadrar" la ecuación.
De la interpretación antes mencionada, y para facilitar el tratamiento estadístico de datos para construir modelos predictivos probados en este contexto, nos acercamos al Método Naïve Bayes, el cual hace una ingenua abstracción de todos estos supuestos lineales y toma las variables categorizadas directamente como atributos mutuamente excluyentes.
Notas
1Esto significa que no
necesitamos poner los modelos separados de la ecuación en escrito para cada subgrupo. Las
variables dicotómicas actúan como los 'switches' que transforman varios
parámetros en SI/NO en una ecuación. Otra ventaja de una variable dummy es que pueden
tratars en clases (niveles o intervalos) aunque sean variables nominales
2El intervalo real de $P$ es [$0,1$], i.e. $Z$ varía en el intervalo ]$-\infty,\infty$[. Así mismo la Logit varía desde $-\infty$ hasta $+\infty$. Nótese que si:
$$Z_i\rightarrow +\infty \Rightarrow e^{-Z_i}\rightarrow 0$$.
$$Z_i\rightarrow -\infty \Rightarrow e^{-Z_i}\rightarrow +\infty$$
3Por ejemplo, un criterio de atraso costoso
podría definirse como un atraso promedio de 15 días o más con respecto al día de pago
programado.
4Cálculos realizados Excel, con los datos de la Tabla $3$. VAR2= Logit $L_i$ y VAR1=$X_i$
4Cálculos realizados Excel, con los datos de la Tabla $3$. VAR2= Logit $L_i$ y VAR1=$X_i$
5La tasa de cambio en la probabilidad de $P$ con respecto a $X_1$ es $\frac{dP}{dX_1}=\beta_1 P(1-P)$, es la elasticidad definida como $\eta=\frac{dP}{dX_1}·\frac{X_1}{P}$
Cálculos realizados Excel
| Estadísticas de la regresión | |||||
| Coeficiente de correlación múltiple | 0,203878465 | ||||
| Coeficiente de determinación R^2 | 0,041566428 | ||||
| R^2 ajustado | -0,09535265 | ||||
| Error típico | 0,023551927 | ||||
| Observaciones | 9 | ||||
| ANÁLISIS DE VARIANZA | |||||
| Grados de libertad | Suma de cuadrados | Promedio de los cuadrados | F | Valor crítico de F | |
| Regresión | 1 | 0,000168396 | 0,00017 | 0,303583896 | 0,598781194 |
| Residuos | 7 | 0,003882853 | 0,00055 | ||
| Total | 8 | 0,004051249 | |||
| Coeficientes | Error típico | Estadístico t | Probabilidad | Inferior 95% | |
| Intercepción | 0,88117949 | 0,016043998 | 54,9227 | 1,73933E-10 | 0,843241463 |
| Variable X 1 | 8,16289E-06 | 1,48151E-05 | 0,55098 | 0,598781194 | -2,68693E-05 |
| Superior 95% | Inferior 95,0% | Superior 95,0% |
| 0,91911752 | 0,843241463 | 0,91911752 |
| 4,3195E-05 | -2,68693E-05 | 4,3195E-05 |
Bibliografía y Videos
[2] ¿Cómo se deduce la fórmula de los coeficientes Mínimos Cuadrados? Sustentación del Modelo, Complemento de Conceptos Matemáticos, José Enrique González Cornejo,Enero del 2012 [3] Distancia de un Punto a una Recta, Sustentación del Modelo, Complemento de Conceptos Matemáticos, José Enrique González Cornejo, Enero del 2012 [4] "Theory of Econometrics", A. Koutsoyiannis, 2º edition McMillan Press 1976 [5] "Basic Econometrics", D.M. Gujarati, 2º 2º edition Mc Graw Hill, 1988 [6] "Investigación DocIRS," Razones, Scoring MYPE" /Planilla Cálculos Logit, 2002 [7] "Presentación Qué es Scoring", BancoEstado, 2002. [8] Video Youtube:Capitulo II: Naïve Bayes ~ Simple (Version Producción), Algoritmo de Clasificación Modelo de Variables Discretas, José Enrique González Cornejo, 2020. [9]Video Youtube:Algoritmo Naïve Bayes Explicado con Tablas Dinámicas Excel, José Enrique González Cornejo, 2020. [10]Video Youtube:Experimento ~ Supervisión y Entrenamiento ~ Inteligencia Artificial ~ Naïve Bayes Learning Machine , José Enrique González Cornejo, 2021. |
Publicaciones Relacionadas
| DocIRS © 1988-2025 |