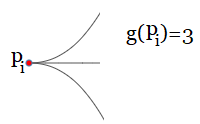|
|
.., habiendo caminado largo
|
| + Ficha Técnica |
| + Explicación Ejemplo |
| + Nótación de Grafos |
|
El Problema de la Ruta Optima
|

 Video
Ruta Optima por Tramos
Video
Ruta Optima por Tramos
|
Introducción
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Agente Viajero
Nótese que, se asume $d(i,j)=0$ cuando $i=j$. Es decir, la diagonal de la
matriz asociada es $0$.
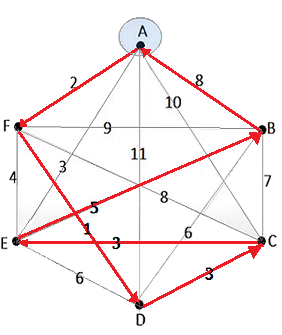
i) Uno por optimización de tramos, el cual presentamos a continuación, como así mismo simulamos el algoritmo DocIRS con un desarrollo de matrices de $4\times4$ hasta $200\times 200$ (Simulación) con valores enteros aleatorios, donde se puede seleccionar el orden de la matriz y decidir si se desea que la matriz sea simétrica o no. Una vez ejecutada la formulación, el sistema despliega la ruta óptima y su costo asociado. (Ver Algoritmo de Dijkstra con Teorema de Bayes ~ Robot Móvil) ii) Un segundo método por permutaciones (todo los posibles caminos, $(N-1)!$, lo hacemos por medio de un algoritmo aleatorio). Este último método "por permutaciones", - resulta ser experimentalmente más exacto-. Sin embargo, no lo utilizamos, dado que cuando el número de puntos es grande, entonces la cantidad de combinaciones es aún mayor. Por tanto, los tiempos de respuesta para lograr la Ruta Optima, son extensos (Por ejemplo, con sólo 10 puntos se tienen 362.880 posibles caminos). Además, este camino resultante es global, dado que se decide por el mínimo del costo total de cada combinación y no por etapas sucesivas. Es decir, presupone que para optimizar se debe realizar la ruta sólo de esa forma. (Ver Ejemplo Simple Permutaciones para la Ruta Optima y probar el Simulator de Permutaciones) ¿En qué orden se debe visitar a los CLIENTES para minimizar el costo total del desplazamiento? Descripción de un Algoritmo de la Ruta Óptima 1. Se elige un punto de partida. (En nuestro caso rotularemos el origen siempre desde el $1$) 2. Se decide ir seguidamente al CLIENTE más cercano. 3. Se va seguidamente a otro CLIENTE, el más cercano (desde el punto de vista de la métrica en cuestión), que no haya sido visitado todavía, hasta que así se hayan visitado todos los CLIENTES, vuelve entonces al punto de partida. 4. Se anota el costo obtenido del recorrido y se vuelve a comenzar eligiendo sucesivamente todos los CLIENTES de la lista como un punto de partida. En síntesis, partimos del origen $1$, y buscamos todas las líneas que inciden en el punto y determinamos el mínimo costo entre los puntos conectados. Se guarda tramo y se realiza recurrentemente el mismo ejercicio, a partir del punto de llegada, eliminando el tramo encontrado en los siguientes pasos. Cuando uno entra en un punto ya ocupamos esa línea de entrada, de ahí, sólo nos queda seleccionar la línea de salida del punto (Ocupamos sólo 2 líneas por punto). La ruta buscada es un ciclo, dado que se retorna al punto de partida rotulado con $1$. Se retorna al punto de partida, una vez que se haya pasado por todos los puntos agendados. Si un punto es equidistante (en costo) de otro y si los costos son mínimos, el algoritmo programado no efectúa pruebas sucesivas con cada uno de los puntos, sino que escoge sistemáticamente aquel que esté primero en su orden. Formalmente, si se considera una matriz de distancias $d_{ij}$ sobre un grafo completo $G$, $$ X_{ij}=\begin{cases}1, & \text{si se usa }i\longrightarrow j\\ 0, & \text{si NO se usa }i\longrightarrow j \end{cases} $$ Donde $X_{ij}$ es una variable dicotómica de decisión y $d(i,j)$ la métrica o ponderación, entonces se puede ilustrar el modelo matemático de selección como: $\text{Min}\sum d_{ij}X_{ij}$
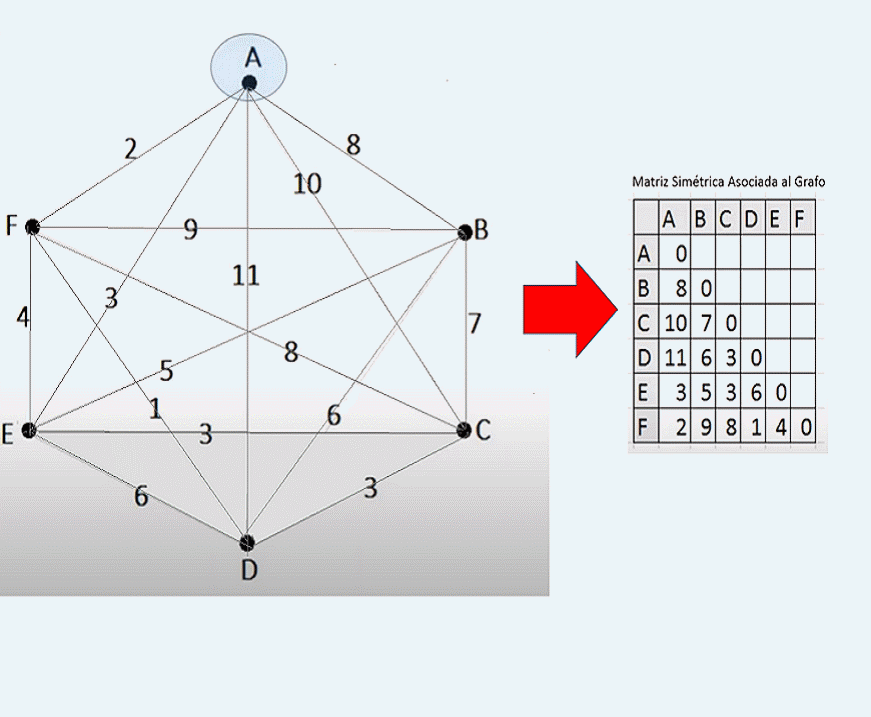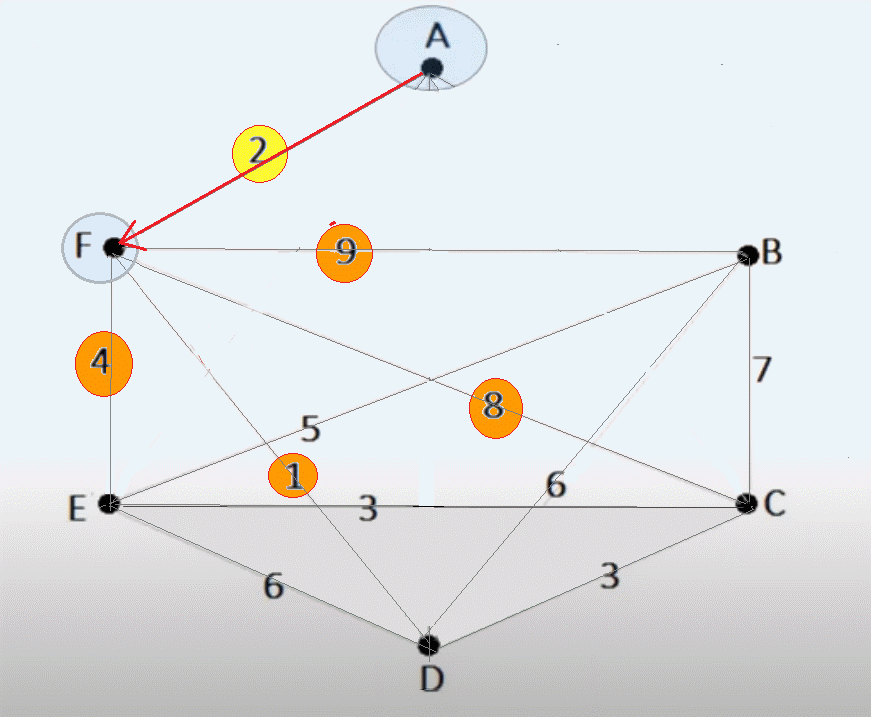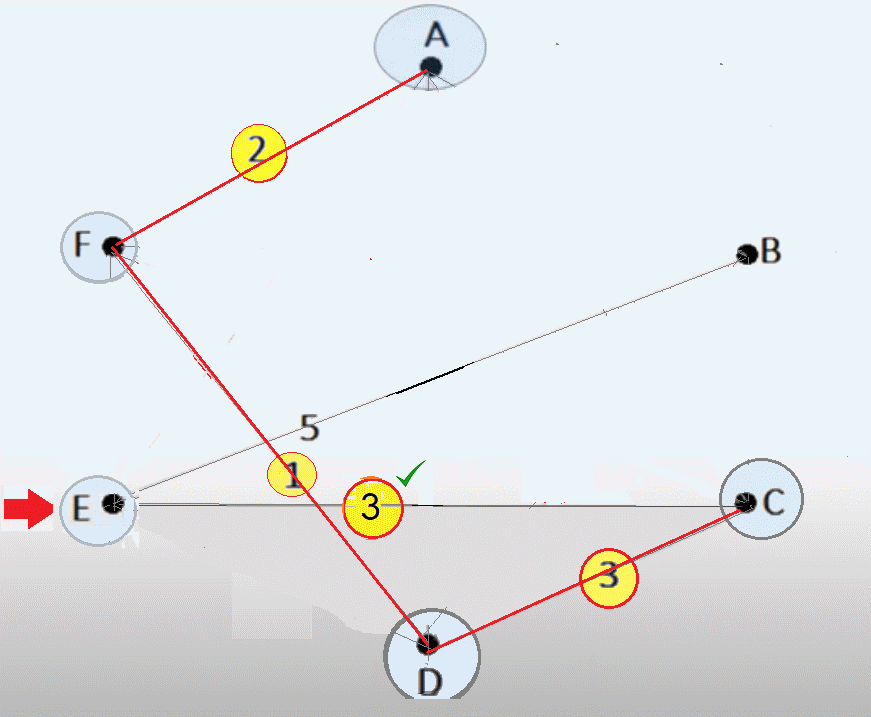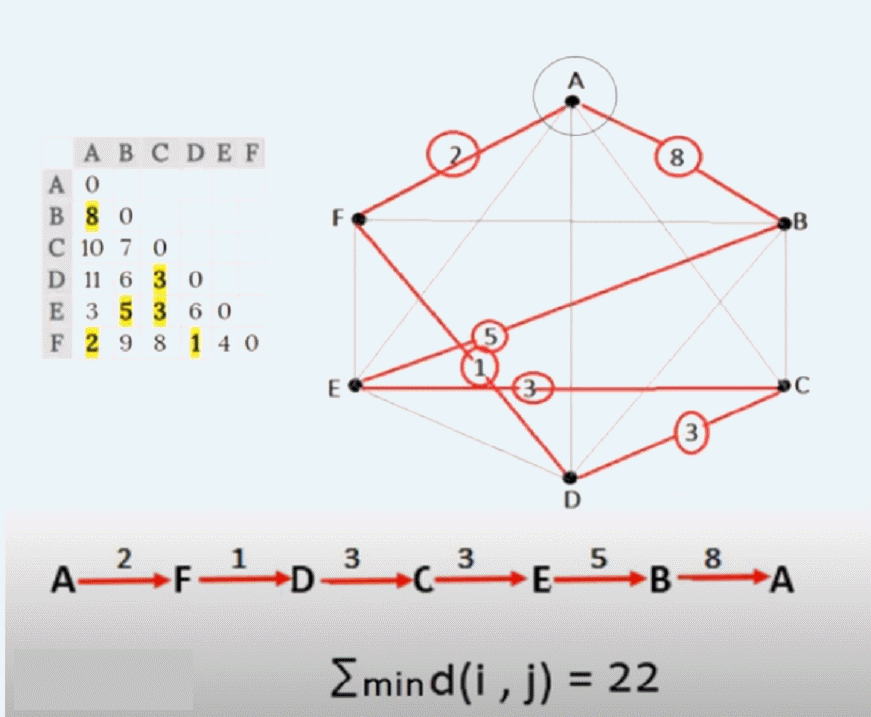
Ejemplo con $7$ CLIENTES.
1. Lista seleccionada con su localización, dada 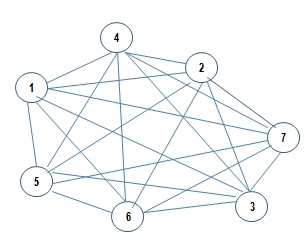
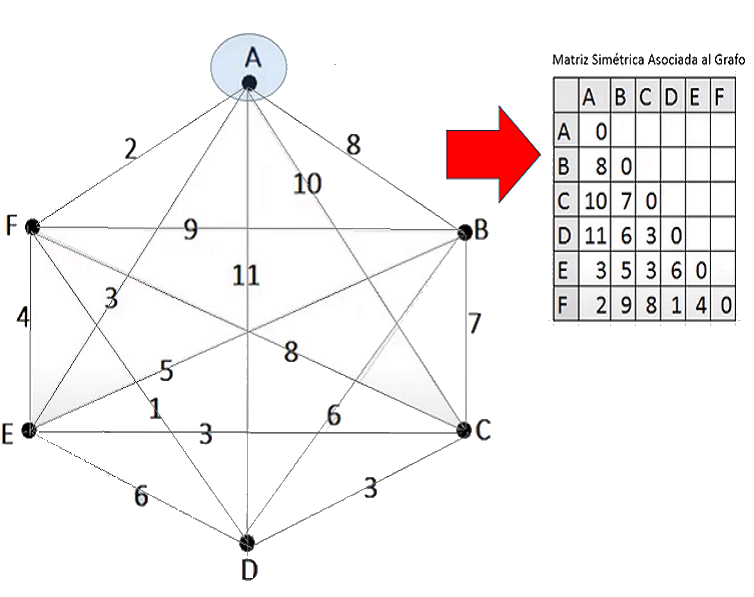
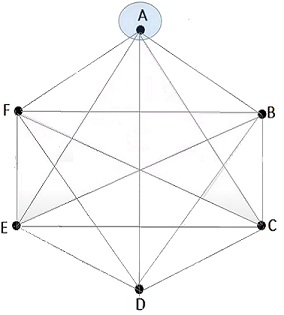
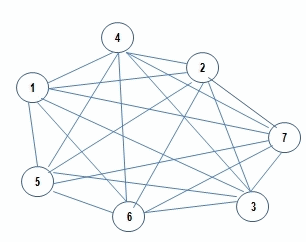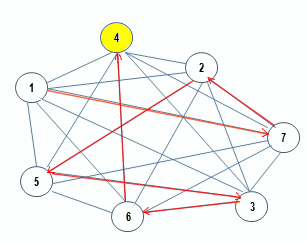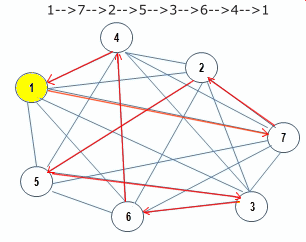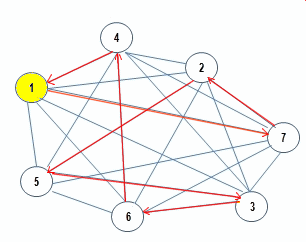
Grafo Completo $G_7$ Nótese que un grafo completo tiene $p=(n-1)$ líneas por punto, donde $n$ es el número de puntos. A continuación sus ponderaciones en su matriz adjunta.
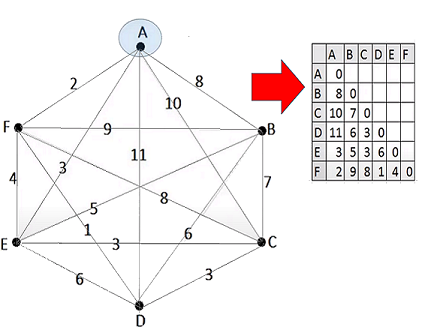
2. La Matriz Adjunta $G_7$ con las distancias o costos entre las
localizaciones establecidas,
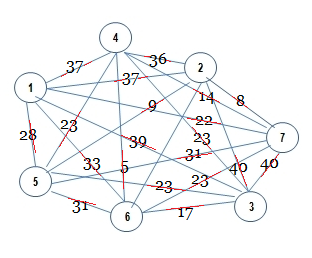
Grafo Completo $G_7$, Ponderado
Valores Enteros Aleatorios entre 1 y 40 de Orden: $7\times7$
(El costo es igual de ida y vuelta) Nótese que la distancia o costo $d(i,j)$=0 cuando i = j.
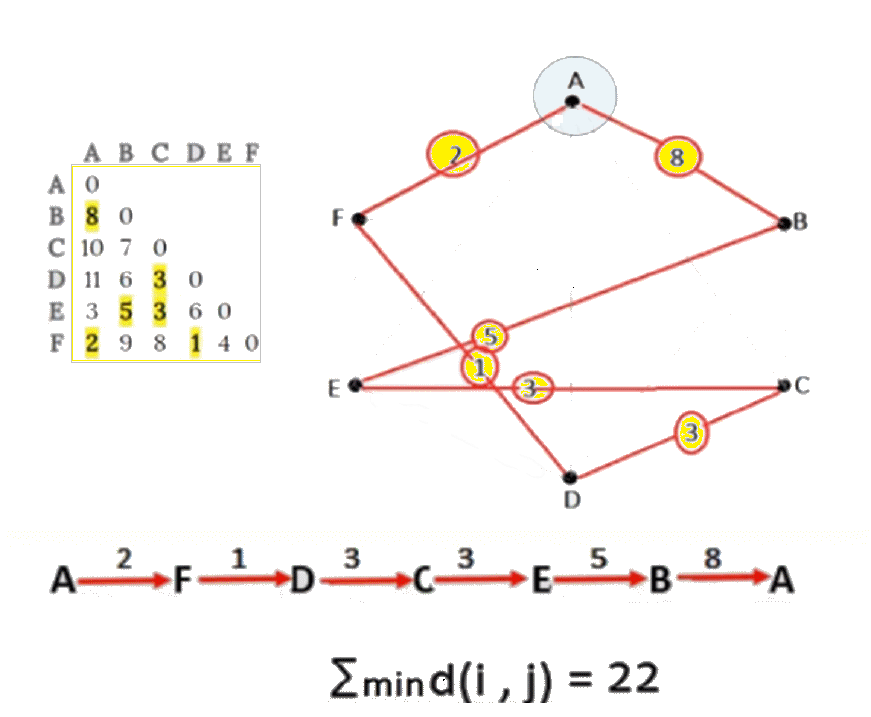
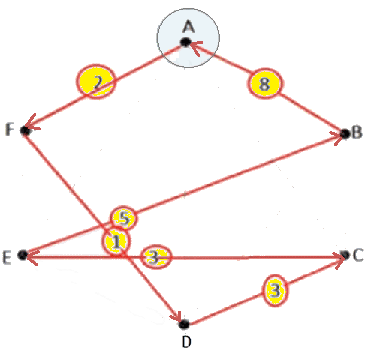
3. La solución
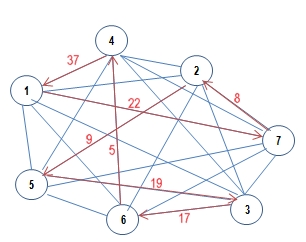 Ruta Optima Resultante
 1  [22] [22]  7 7  [8] [8]  2 2  [9] [9]  5 5  [19] [19]  3 3  [17] [17]  6 6  [5] [5]  4 4  [37] [37]  1 1
Minimo$\sum [f_{i}]= 92$ 4. Formalización del algoritmo utilizado El algoritmo con que se resolvió el problema Ruta Óptima para Visitar CLIENTES, es mediante una técnica matemática llamada Programación Dinámica1 , dado que la solución se aproxima tomando decisiones en etapas sucesivas y de este modo es posible retomar la ruta en diferentes períodos, asumiendo que el costo o distancia es constante ($d(0,j) \forall j=1,2,\dots N$). Es decir, desde el origen hasta cualquier dirección (o nodo) de la lista de CLIENTES a visitar. (ver Programación con Diseño Modular o Top-Down) El problema se abordó, bajo las siguientes condiciones:
i) La solución se logra a través de una secuencia de
decisiones, una en cada etapa.
Sea $D$={$d(i,j)$} la matriz cuadrada de orden $n$, donde cada $d(i,j)\in
\mathbb R$ es el costo o distancia de ir desde $i$ hasta $j$. La matriz $D$
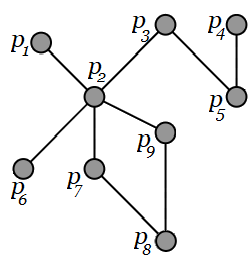
tiene un grafo completo2
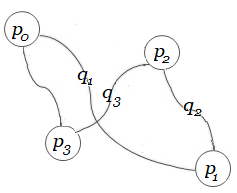
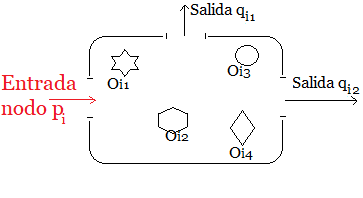
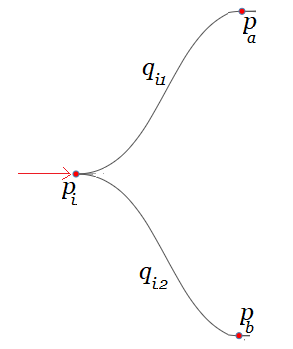
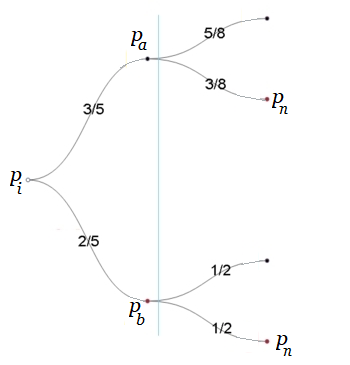
$G$ asociado. Sea $\unicode{123}p_{i}\unicode{125}$ el conjunto de los $n$ puntos (o nodos) del grafo $G$.($n\in \mathbb N$) Sea el punto $p_{1}\in \unicode{123}p_{i}\unicode{125}$ el punto de partida. (Arbitrariamente lo localizamos en el rotulo $1$ del LISTA DE CLIENTES SELECCIONADOS). Entonces, existen $(n-1)!$ caminos que pasan una sola vez por cada punto $p_{i}$, con $p_{i}\ne p_{1}$. Sea $Q=\unicode{123}q_{i}\unicode{125}$ el conjunto de todos los posibles caminos hamiltonianos3 que se pueden obtener sobre el grafo $G$, partiendo de $p_{1}$. (Nótese que en cada camino $q_i$, todos los puntos intermedios entre el primero y el ultimo, tiene sólo dos líneas que inciden: una línea que entra y otra que sale.) Sea $C_{i}$, el costo de cada sumatoria $\sum d(i,j)$ que se obtiene de cada camino $q_i \in Q$.
Sea $F=\unicode{123}f_{i}\unicode{125}$ el conjunto de puntos asociados al
camino que representa el $C_{m}=min(C_{i}, F)$. Es decir, $C_m$ $f_{1}
→ f_{2} →f_{3} →...f{n}$ (Nótese que $f_{1}=p_{1}$, i.e. $f_i$: la
política de costo mínimo de la etapa. Donde se establece la siguiente
restricción:
Entonces la relación recursiva dinámica se expresa como: Para cada uno de
los
Luego, $ \exists q_{0} \in Q \text{|} q_{k}=f_{k}i$, cuyo costo o distancia
es $C_m$
Explicación de la Rutina Computacional
Valores Utilizados en la Métrica
Con grandes cantidades de nodos a visitar, se debe trabajar con matrices de magnitud mayor. A veces con matrices que representan diferentes métricas (distancias, costos, adyacencia, difcultad, tiempo,etc...) combinadas con diversas restricciones. Canal Youtube Notas Complementarias Adjuntas
Bibliografía:
|