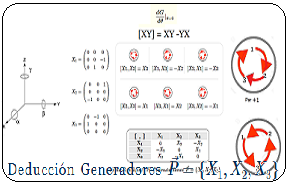
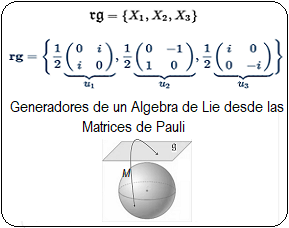
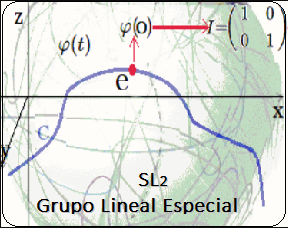
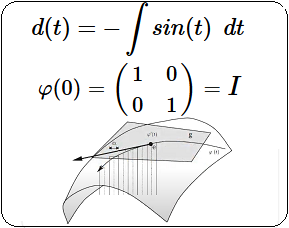
¿Qué es un Grupo de Lie?
José Enrique González Cornejo
|
Introducción
Dentro del álgebra abstracta, un Grupo de Lie es un tipo especial de grupo algebraico que posee propiedades continuas y diferenciables.
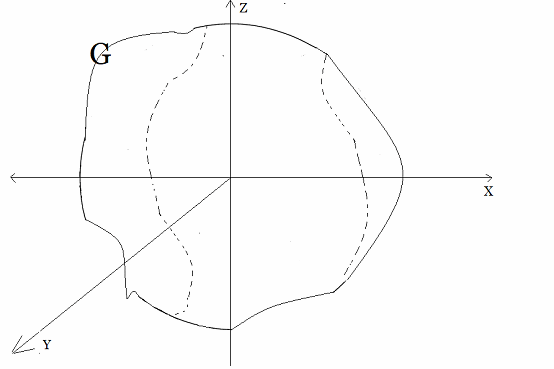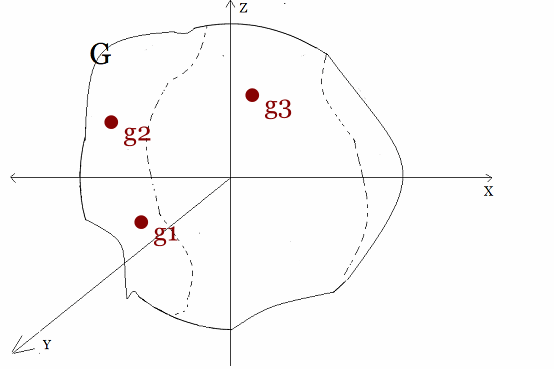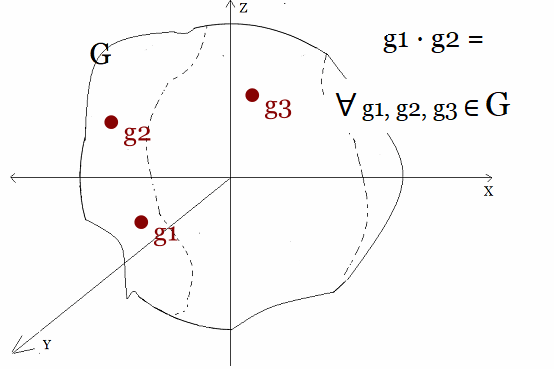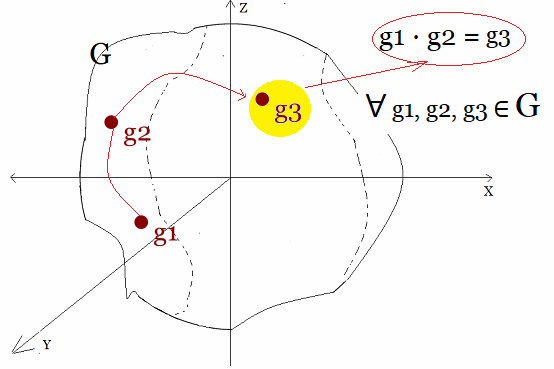 Grupo $(G,·): g_1,g_2,g_3\in G$ Ahora, lo que distingue a un Grupo de Lie es que tiene una estructura diferenciable. Esto significa que las operaciones del grupo (composición y multiplicación) y las funciones que mapean los elementos del grupo deben ser continuas y diferenciables. Es decir, son derivables en relación con parámetros continuos10 En otras palabras, un Grupo de Lie es un grupo y una variedad diferenciable13 o manifold al mismo tiempo. 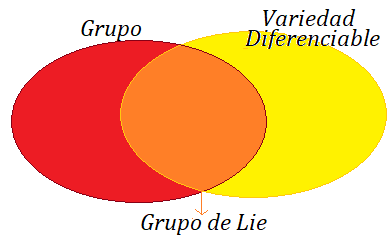 Grupo de Lie: Grupo y Manifold Por cierto, en un Grupo de Lie, es posible conectar dos elementos del grupo a través de una curva suave dentro del grupo. Esta propiedad de conexión continua es fundamental en muchas aplicaciones, especialmente en física y Geometría Diferencial  .
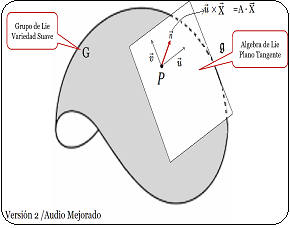
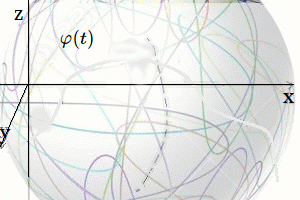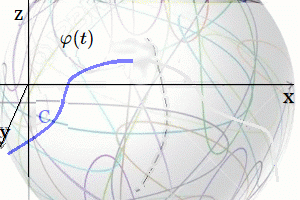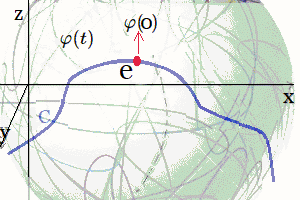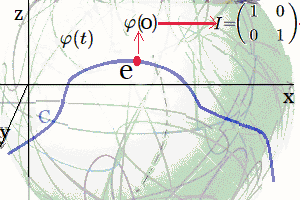  $\large{\varphi(t)}$: Curva $C$ sobre Variedad SuaveTodo Grupo de Lie se puede asociar con un álgebra de Lie2, que es un espacio vectorial con una operación propia llamada conmutador o corchetes de Lie 3. El álgebra de Lie captura las propiedades de la estructura del grupo y es útil para estudiar la transformación local y la simetría. Luego, un Grupo de Lie es una estructura matemática que combina las propiedades de los grupos y las variedades. Lo que significa que sus elementos pueden describirse mediante coordenadas y se pueden aplicar operaciones de cálculo diferencial.
| Definición Matemática de un Grupo de Lie
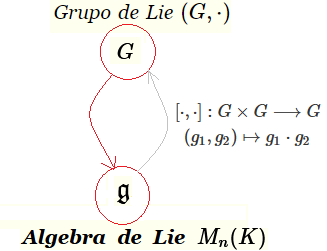|  Grupo de Lie $G$ $\longrightarrow$ Algebra de Lie $\large{\mathfrak {g}}$ 6
A continuación se explica matemáticamente cómo se define un grupo de Lie:
|
A partir de un Grupo de Lie $G$, en tanto es una variedad diferenciable4 topológica o una Variedad Suave ("Manifold" o superficie como un plano, un círculo, una esfera, u otras superficies suaves en diferentes dimensiones) 5
Luego, un Grupo de Lie $G$ es:
|
Es decir, $ G $ debe tener la estructura de una variedad diferenciable de dimensión finita:
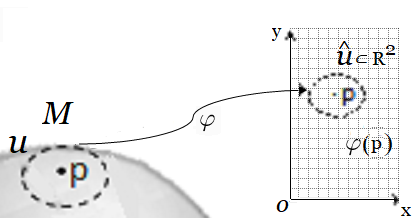 Variedad Superficie Esfera (carta) - Plano Cartesiano
|
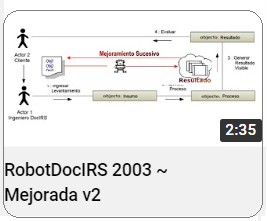
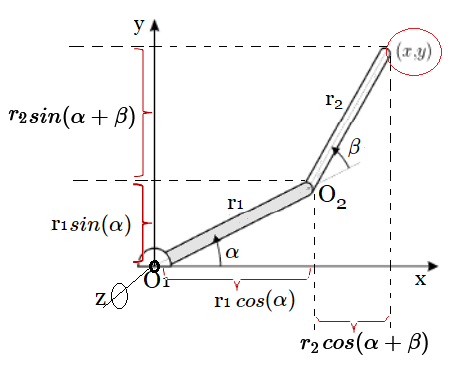
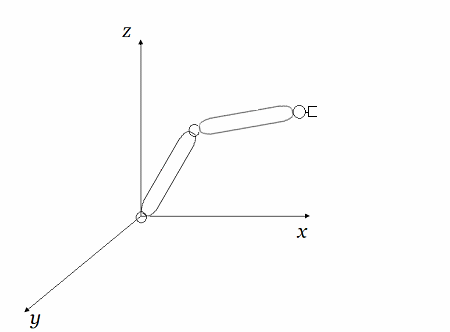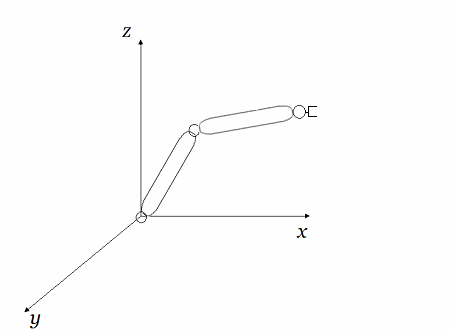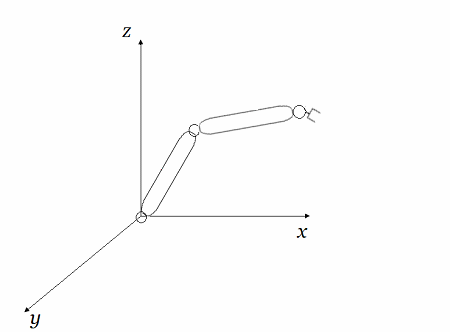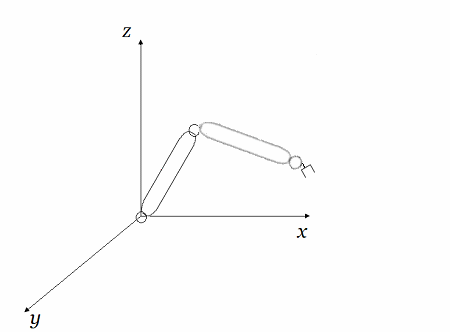
Aplicación Grupo de Lie Por ejemplo, una aplicación de los Grupos de Lie en ingeniería se encuentra en la robótica. (Ver Algebra de Lie $M_n(K)$ - Aplicaciones ~ Formalización )
Los Grupos de Lie se utilizan para modelar y analizar los movimientos de los robots. Por ejemplo, en la cinemática de un brazo robótico, se puede utilizar la teoría de los Grupos de Lie para describir cómo las diferentes articulaciones se mueven y cómo esto afecta la posición y orientación del extremo del brazo. Esto permite diseñar controladores que puedan mover el brazo de manera precisa y eficiente.
|
|
Los Grupos de Lie son esenciales en muchas áreas de la física teórica, donde se utilizan para describir simetrías y transformaciones de campos físicos. También son fundamentales en la teoría de grupos en matemáticas, donde se estudian en detalle y se clasifican para comprender su estructura y propiedades. Origen e Historia Los Grupos de Lie deben su nombre al matemático noruego Sophus Lie, quien los introdujo en el siglo XIX. Sophus Lie estaba interesado en estudiar las simetrías continuas de las ecuaciones diferenciales, algo que se puede considerar una extensión de la Teoría de Grupos, que tradicionalmente se aplicaba a simetrías discretas. Este brillante matemático noruego vivió entre 1842-1899, desarrollando la idea de una variedad de propiedades geométricas y analíticas, que se explicaban mediante la utilización del concepto de simetría continua. Este estudio, lo indujo a desarrollar lo que hoy se conoce como Grupos de Lie. La invariabilidad de la métrica en ciertas transformaciones continuas, bajo determinadas estructuras geométricas y ecuaciones diferenciales le permitió observar que estas transformaciones formaban grupos. Es decir, conjuntos con una operación binaria que cumplen las condiciones algebraicas de esa estructura algebraica1. Sophus Lie, logró descubrir que estos grupos, no solo son una estructura algebraica, sino que también poseen una estructura suave o diferenciable, esto implicaba que es posible describir mediante funciones continuas y diferenciables. De ahí que, se convirtió en una herramienta importante para el desarrollo de varias áreas de las matemáticas y la física. Hoy es fundamental para el estudio y aplicación de la Física Teórica, la Geometría Diferencial, Teoría de Control e investigación matemática en diversas disciplinas científicas y de la ingeniería. Teoría de Galois Es necesario remarcar, que previamente a los Grupos de Lie se desarrolló una nuevo enfoque novedoso y moderno por el talentoso joven matemático francés Évariste Galois (1811-1832) en el mismo siglo XIX, que tuvo una influencia significativa en muchos campos de la matemática, incluyendo el trabajo de Sophus Lie en los Grupos de Lie. En efecto, la teoría de Galois estudia las raíces de polinomios y las simetrías de estas raíces. Específicamente, se enfoca en las estructuras algebraicas conocidas como "Grupos de Galois", que describen cómo se pueden permutar las raíces de un polinomio sin cambiar la estructura de las relaciones entre ellas. Este trabajo de Galois sirvió a Sophus Lie en los ámbitos de las Simetrías y Transformaciones, Estructuras Algebraicas, Correspondencia entre Álgebra y Geometría, Métodos de Resolución y otras ideas metodológicas. En otros términos, la manera en que Galois utilizó los grupos para entender simetrías algebraicas inspiró a Sophus Lie a utilizar grupos continuos, llevándolo al desarrollo de los Grupos de Lie.  Cubo de Rubik Ejemplo de Grupo Simétrico de Permutación
|
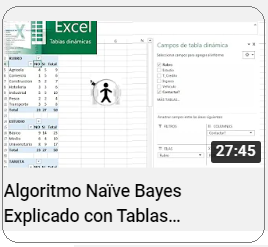
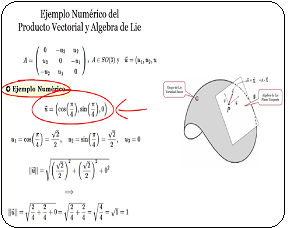
Ejemplo Polinomio Simple Grupo de Galois A continuación, se explica con un ejemplo simple cómo la Teoría de Galois ayuda a encontrar las raíces o ceros de un polinomio, y cómo estas raíces forman una estructura algebraica de grupo. Sea $f(x)$ el polinomio cuadrático en $\mathbb {R}$: $$ f(x) = x^2 - 2 $$ Donde se mostrará que las raíces del polinomio $f(x)$ y sus permutaciones forman un Grupo de Galois. Esto implica que este grupo captura las simetrías algebraicas de las raíces, mostrando cómo se relacionan entre sí a través de permutaciones. En efecto, se resuelve la ecuación $ x^2 - 2 = 0 $: $$ x^2 = 2 \quad\implies \quad x = \pm \sqrt{2} $$ Luego, las raíces o ceros del polinomio son {$ \sqrt{2}, -\sqrt{2} $}. Las raíces de un polinomio $ f(x) $ satisfacen ciertas relaciones algebraicas derivadas del polinomio. Por ejemplo, si $ f(x) $ es un polinomio de grado $ n $ con coeficientes en un campo $ K $7, entonces: $$ f(x) = (x - \alpha_1)(x - \alpha_2) \cdots (x - \alpha_n) $$ De modo que, en el presente ejemplo con un polinomio de grado $2$, con coeficientes en el campo de las reales, se tiene que: $$ f(x) =x^2 - 2 = 0\quad\Rightarrow \quad (x - \sqrt{2})(x + \sqrt{2})=0\\ \Rightarrow \quad x - \sqrt{2}=0\quad \lor \quad x + \sqrt{2}=0\\ \Rightarrow \quad x_1=\sqrt{2}\quad,\quad x_2=-\sqrt{2} $$ La Teoría de Galois se interesa en cómo podemos permutar estas raíces sin cambiar las relaciones algebraicas entre ellas, i.e. las permutaciones de estas raíces que dejan invariante el polinomio $f(x)$ constituyen un grupo. En este ejemplo, las permutaciones posibles son intercambiar $ \sqrt{2} $ y $ -\sqrt{2} $, o dejar ambas raíces en su lugar. Estas permutaciones forman un grupo conocido como Grupo de Galois de ese polinomio 8. Por tanto, para el polinomio $ f(x) = x^2 - 2 $, las permutaciones de las raíces forman el Grupo de Galois $G$ con la operación binaria composición de permutaciones "$\Large{·}$" y sus simetrías son:
El Grupo de Galois $ G $ del polinomio $f(x)$ tiene dos elementos: $ \{e, \sigma\}$ que cumplen las propiedades de un grupo de permutación. Dado que $G$ es un conjunto de permutaciones (reordenamientos) que es cerrado, tiene un elemento identidad, tienen inversa y es asociativo. Para ese efecto, se define la operación binaria composición de permutaciones que combina los elementos del grupo. Operación binaria que generalmente se utiliza en el contexto de la Teoría de Galois. 
|
Síntesis En síntesis se dice que un Grupo de Lie es una estructura algebraica que combina las propiedades de un grupo de transformaciones continuas (como rotaciones o traslaciones) con las propiedades de una variedad diferenciable (espacios suaves y curvos). El presente artículo intentó describir las características centrales de un grupo de Lie:
ii) Un grupo de Lie es una variedad diferenciable, lo que significa que es un espacio suave y curvo. Además, se puede describir utilizando coordenadas locales y funciones suaves. iii) La operación de grupo (es decir, la multiplicación de elementos del grupo) debe ser una función suave en la variedad. (Ver por ejemplo $SO(2)$ 'Special Orthogonal Group of Dimension 2) iv) La operación inversa de un elemento del grupo también debe ser una función suave.  Hormigas sobre piedra. Superficie curva y lisa Los grupos de Lie son una herramienta matemática fundamental para otras ciencias exáctas y naturales, ya que describen simetrías continuas en sistemas físicos y proporcionan un marco para estudiar las propiedades de sistemas físicos y sus transformaciones. Por ejemplo, el Grupo Lineal Especial $Sl_2$ que es un grupo de Lie muy característico y se presta para generar un Algebra de Lie, como así mismo para ilustrar su estructura algebraica son sus elementos de transformación lineal mediante la llamada Teoría de las Representaciones. Es importante destacar que los grupos de Lie pueden ser finitos o infinitos, ya sea de dimensiones finitas o infinitas. |
Grupo de Lie - Enfoque Geométrico