|
Grupos Diédricos desde Arquímedes
Simetría y Reflexión
José Enrique González Cornejo
mayo 2025
|
Introducción A partir de la presentación del Método de Arquímedes, desarrollada en el artículo y video Cálculo de PI ~ Algoritmo de Arquímedes , donde se expone un algoritmo que aproxima con alta precisión el valor de la constante $\large{\pi}$, surge naturalmente el concepto de grupos diédricos. En dichas publicaciones, —tanto el artículo como el video—, se observa que al duplicar sucesivamente polígonos regulares inscritos en una circunferencia, se genera un Grupo de Permutación, conocido como $ D_n $ o grupo diédrico de orden $ 2n $. Este grupo es finito para todo $ n > 3 $, con $ n \in \mathbb{N} $, donde $ n $ representa el número fijo de lados del polígono, es decir, simetrías discretas. 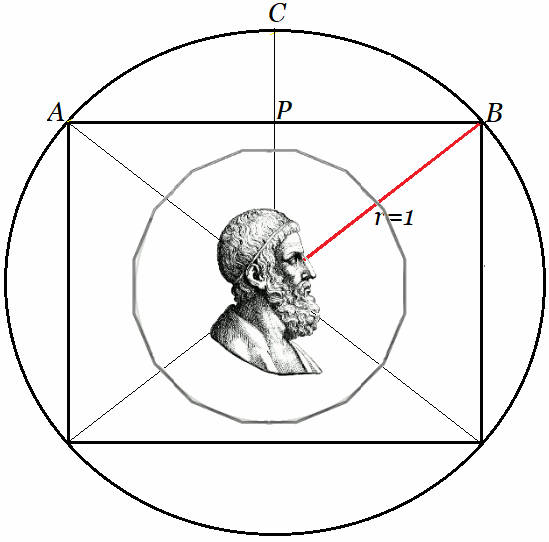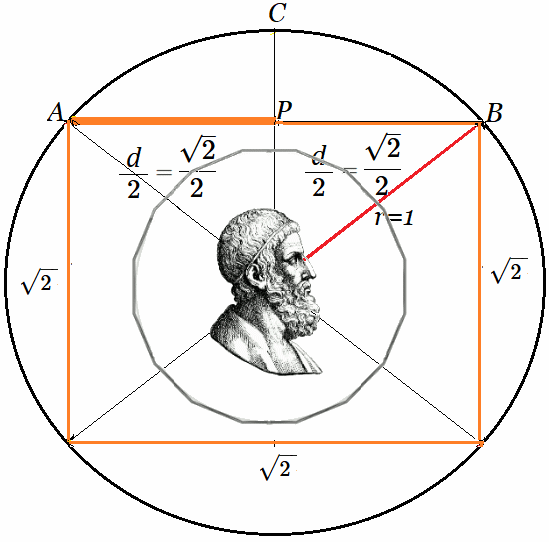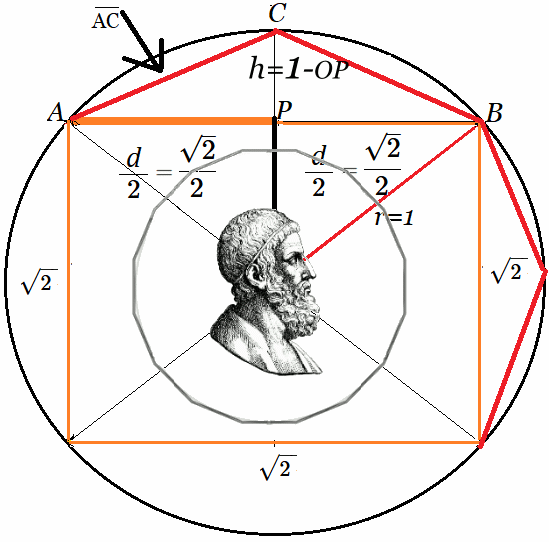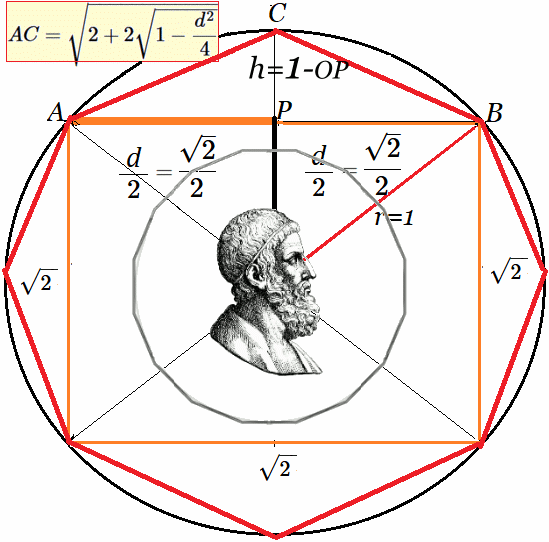
Cálculo de $\large{\pi}$ ~ Algoritmo de Arquímedes El grupo $ D_n $ describe las simetrías (rotaciones y reflexiones) de un polígono regular de $ n $ lados. Al considerar una familia numerable de estos grupos, como en el caso de $ \{D_4, D_8, D_{16}, D_{32}, \dots\} $, obtenemos una secuencia infinita de grupos finitos, todos relacionados con las simetrías de los polígonos inscritos en la circunferencia. En general, una transformación que mapea uno a uno un conjunto sobre sí mismo y que conserva ciertas propiedades, forma un grupo. Los grupos de simetría y reflexión en este contexto se generan al girar un polígono regular de forma que se superpone perfectamente sobre sí mismo. Además, existen ejes de reflexión que pasan por vértices y por lados opuestos, dividiendo al polígono en partes con simetría axial. Cada polígono inscrito, —al ir duplicando sus lados—, da lugar a un grupo, ya que el conjunto de sus rotaciones y reflexiones:
- Posee una operación binaria cerrada (composición de transformaciones). - Tiene un elemento neutro (la rotación de $ 0^\circ $). - Cada transformación posee su inversa. Por lo tanto, el grupo $ D_n $ puede interpretarse como un subgrupo del grupo simétrico $ S_n $, lo cual lo convierte en un Grupo de Permutación. Cuando tratamos con familias numerables de tales grupos, por ejemplo: $D_{16}$ Polígono regular de 16 lados rotando Nótese que el polígono de $16$ lados está inscrito en un círculo y rota lentamente de manera continua (giro), los nodos o vertices (rotulados con letras) se permutan simétricamente y cambian de vértice uno a uno sincronizados con el giro, donde cada cambio es una acción de rotación que va reetiquetado y preservándose simétricamente. Las rotaciones continuas de un objeto invariante constituyen un Grupo de Lie , no así el objeto $D_n$ fijo que no posee una estructura diferenciable . Rotaciones y Reflexión Supongamos los vertices numerados {$1,2,3,\dots , n-1, n$} en la dirección de giro de las agujas del reloj. De donde los mapeos de $D_n$ son congruentes que preservan la distancia de la figura sobre sí misma, i.e. estas transformaciones preservan la forma del polígono, aunque cambien la posición de los vértices. Luego, todas las simetrías y reflexión pueden estar representados como permutaciones por matrices de transformaciones del grupo diédrico $ D_n $, utilizando como base un polígono regular con vértices numerados del $1$ al $ n $. A fin de simplificar la modelación de la simetría y reflexión de grupo diédricos, se hará con $D_4$, i.e. un cuadrado, describiendo sus características y propiedades. (Ver [B12] Video Grupos de permutaciones ~ Universidad Abierta y a Distancia de México ~ Distrito Federal, México, 2015 ~ Yannina Ovalle Rodriguez )
En el caso de $D_4$, los generadores típicos son $\large{r_0}$ una rotación de $\large{\frac{\pi}{2}}$ en sentido horario y $\large{s_k}$ en una reflexión respecto a un eje de simetría. Es decir, cualquier elemento de este grupo se puede expresar como una composición de $\large{r}$ y $\large{s}$. $D_4$ Polígono regular de 4 lados rotando En efecto, las rotaciones forman un subgrupo cíclico de orden $ n $. Cada rotación $ r_k $ (con $ k = 0, 1, ..., n-1 $) corresponde a un desplazamiento de los vértices en $ k $ posiciones en sentido horario. $$ r_k: i \mapsto (i + k) \mod n $$ Por ejemplo, para $ n = 4 $: La representación gráfica del grupo $ D_4 $ en sentido horario: $\require{AMScd}$ \begin{CD} 1 @> >> 2\\ @V V V @VV V\\ 3 @>> > 4 \end{CD} $$\implies$$
- $ r_1 $: $ (1,2,3,4) \to (4,1,2,3) $ - $ r_2 $: $ (1,2,3,4) \to (3,4,1,2) $ - $ r_3 $: $ (1,2,3,4) \to (2,3,4,1) $ Donde ($r_0$ es la identidad) su representación matricial de permutación $ R_k $ de tamaño $ n \times n $, tiene la posición $ (i,j) $ es $1$ si el vértice $ j $ se mapea al vértice $ i $, y $0$ en otro caso. Por ejemplo para $ n=4 $, la matriz de rotación $ r_1 $: $$ R_1 = \begin{bmatrix} 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} $$ Las Rotaciones por extensión:
Rotación $0°$ (identidad): $$ \begin{pmatrix} 1 & 2 & 3 & 4 \\ 1 & 2 & 3 & 4 \end{pmatrix} $$ Rotación $90°$ (una posición a la derecha): $$ \begin{pmatrix} 1 & 2 & 3 & 4 \\ 4 & 1 & 2 & 3 \end{pmatrix} $$ Rotación $180°$: $$ \begin{pmatrix} 1 & 2 & 3 & 4 \\ 3 & 4 & 1 & 2 \end{pmatrix} $$ Rotación $270°$: $$ \begin{pmatrix} 1 & 2 & 3 & 4 \\ 2 & 3 & 4 & 1 \end{pmatrix} $$ Reflexiones $D_4$ Se generan $ n=4 $ reflexiones, y su eje puede ser:
- Una línea que pasa por el centro de un lado y el centro. $$ \large{ \begin{array}{ccc} & s_1 & \\ & | & \\ s_0 & \xrightarrow{\ r_0\ } & s_2 \\ & | & \\ & s_3 & \end{array} } $$ El efecto depende del eje elegido. Las reflexiones invierten el orden de los vértices, respetando su simetría. - Reflexión vertical (eje pasa por vértices $1$ y $3$): $$ (1, 2, 3, 4) \to (1, 4, 3, 2) $$ - Reflexión diagonal (eje pasa por lados entre vértices): $$ (1, 2, 3, 4) \to (3, 2, 1, 4) $$ Para su representación matricial también se usa una matriz de permutación para cada reflexión. Por ejemplo para reflexión que intercambia $2$ y $4$ (manteniendo $1$ y $3$): $$ S = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ \end{bmatrix} $$ Cada matriz de reflexión es involutiva. Es decir, $$ S \cdot S = I $$ Conclusión Formalmente el grupo diédrico \( D_n \) puede definirse como: $$ D_n = \langle r,\quad s \mid r^n = e,\quad s^2 = e,\quad s·r·s = r^{-1} \rangle $$
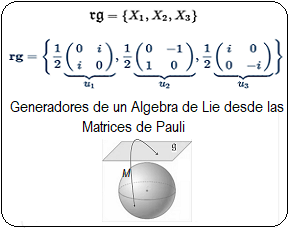
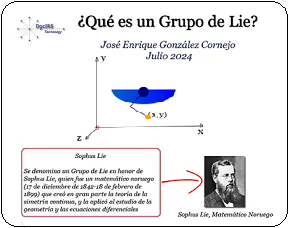
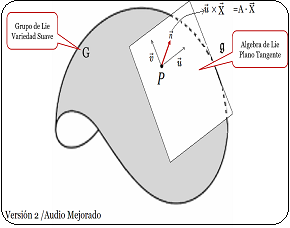
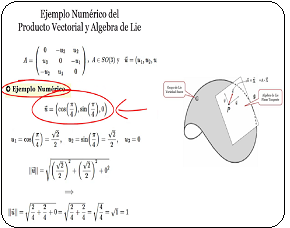
Todas las matrices del grupo $ D_n $ son ortogonales y preservan distancias y ángulos. Las rotaciones forman un subgrupo cíclico de orden $ n $. El grupo completo $ D_n $ tiene $ 2n $ elementos: $\large{ \{ r_k, s_k \} }$, donde $ \large{ s_k = r_k \cdot s_0 } $ y satisface la relación: $$ \large{s^2 = 1,\quad s·r = r^{-1}s} $$ En síntesis, la estructura $D_4$ tiene $8$ elementos ($4$ rotaciones más $4$ reflexiones). Sus operaciones binarias se conforman como composición de movimientos, es un grupo no abeliano cuyos subgrupos de rotaciones {$\large{r_0,r_1,r_2,r_3}$} es cíclico, donde cada reflexión genera subgrupos de orden $2$. Estos grupos $D_n$ no son grupos de Lie, dado que los grupos de Lie son grupos topológicos diferenciables y tienen una estructura suave, como la del espacio real $R^n$ en algún entorno local. En cambio el grupo $D_n$ es finito, no posee una estructura diferenciable ni topológica continua y no puede parametrizarse con variables reales de manera suave. En efecto, los grupos de Lie son grupos topológicos diferenciables, con una operación interna binaria, pueden describirse con coordenadas continuas, derivables y tienen una estructura suave, como la del espacio real $\mathbb {R^n} $ en algún entorno local. En cambio los grupos $D_n$ son finitos con solo $2n$ elementos, su estructura no es diferenciable ni topológica continua, no pueden ser parametrizado con variables reales de manera suave. |
|||||||||||||||||||||