Cálculo de PI
Algoritmo de Arquímedes
José Enrique González Cornejo
noviembre 2015
|
Video Asociado
|
Introducción
La constante pi, - denotada con la letra griega $\large{\pi}$, es la razón entre el perímetro de una circunferencia y su diámetro, definida en el plano. $$ \pi = \frac{\mathcal{\small{C}}}{\mathcal{\small{D}}} \qquad \mathcal{\small{ C,D}} \in \mathbb {R} $$ Donde, $ \mathcal{\small{C}} $ es el perímetro y $ \mathcal{\small{D}} = 2r $ es el diámetro de la circunferencia de radio $ r $. Este artículo tiene como objetivo mostrar el algoritmo utilizado para calcular el valor de $\large{\pi}$, a través de una sencilla función en JavaScript. La función, que hemos llamado Calculo_Pi(), aproxima la constante siguiendo el método geométrico desarrollado por el matemático griego Arquímedes1, cuyo procedimiento explicaremos a continuación. A lo largo de la historia, el valor de $\large{\pi}$ ha sido aproximado mediante diversos enfoques. En este artículo nos centraremos exclusivamente en el método de Arquímedes, sin adentrarnos en conceptos del Cálculo Infinitesimal o Integral (como límites, trigonometría o series) ni en las herramientas de la matemática moderna. Sin embargo, cabe destacar que este ingenioso procedimiento ya anticipa, de cierta forma, las bases del Cálculo Diferencial que conocemos hoy. Ademas, los polígonos regulares2 inscritos en una circunferencia de radio $r=1$ son grupos de simetría3 porque admiten un conjunto bien definido de rotaciones y reflexiones que los dejan invariantes. Estas transformaciones forman un grupo algebraico llamado grupo diédrico $D_n$, que es uno de los ejemplos clásicos de simetría en geometría y teoría de grupos. Orden del Artículo Se presenta:
Animación Gráfica Concepto  4 Función Javascript y Estimaciones5
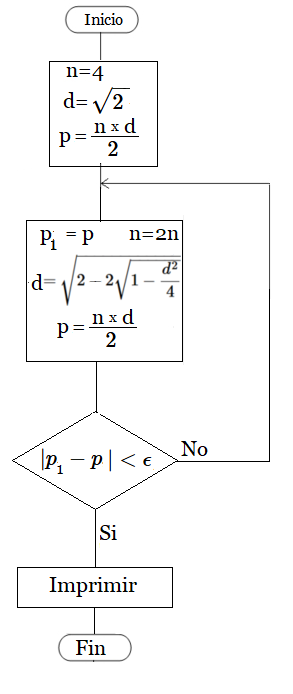
Función Calcula_Pi(9) en Javascript6 Tabla con Iteraciones La siguiente tabla muestra la aplicación de la función Calculo_Pi(m) , con $m=1,2,...9$. Donde el valor epsilon en cada fila toma el valor $10^{-m}$. Se publican también en esta Tabla#1 los valores intermedios $n, d, \large{\pi}$ estimados y error, -o diferencia en valor absoluto del $\large{\pi}$ de la iteración anterior con el actual-. Se visualiza en los valores estimados, que a partir de $\large{\epsilon 10^{-9}}$ el error es muy cercano a cero. Cálculo de los primeros 5 valores de la sucesión definida por la función: $$ d_1 = \sqrt{2} \approx 1.414213562 $$ $$ d_2 = \sqrt{2 + 2\sqrt{1 - \frac{d_1^2}{4}}} $$ $$ = \sqrt{2 + 2\sqrt{1 - \frac{2}{4}}} = \sqrt{2 + 2\sqrt{0.5}} = \sqrt{2 + 2 \cdot 0.707106781} = \sqrt{2 + 1.414213562} = \sqrt{3.414213562} \approx 1.847759065 $$ $$ d_3 = \sqrt{2 + 2\sqrt{1 - \frac{d_2^2}{4}}} \Rightarrow d_2^2 \approx 3.414213562 \Rightarrow \frac{d_2^2}{4} \approx 0.853553390 $$ $$ \Rightarrow \sqrt{1 - 0.853553390} = \sqrt{0.146446609} \approx 0.382683432 $$ $$ d_3 = \sqrt{2 + 2 \cdot 0.382683432} = \sqrt{2 + 0.765366864} = \sqrt{2.765366864} \approx 1.662939225 $$ $$ d_4 = \sqrt{2 + 2\sqrt{1 - \frac{d_3^2}{4}}} \Rightarrow d_3^2 \approx 2.765366864 \Rightarrow \frac{d_3^2}{4} \approx 0.691341716 $$ $$ \Rightarrow \sqrt{1 - 0.691341716} = \sqrt{0.308658284} \approx 0.555570233 $$ $$ d_4 = \sqrt{2 + 2 \cdot 0.555570233} = \sqrt{2 + 1.111140466} = \sqrt{3.111140466} \approx 1.763842529 $$ $$ d_5 = \sqrt{2 + 2\sqrt{1 - \frac{d_4^2}{4}}} \Rightarrow d_4^2 \approx 3.111140466 \Rightarrow \frac{d_4^2}{4} \approx 0.777785116 $$ $$ \Rightarrow \sqrt{1 - 0.777785116} = \sqrt{0.222214884} \approx 0.471396737 $$ $$ d_5 = \sqrt{2 + 2 \cdot 0.471396737} = \sqrt{2 + 0.942793474} = \sqrt{2.942793474} \approx 1.715457220 $$ $$ \pi_n \approx \frac{n \cdot d_n}{2} $$
Tabla de Iteraciones
Arquímedes y su Contexto El algoritmo de la función desarrollada, está basado en siguiendo el enfoque geométrico que Arquímedes desarrolló alrededor de 300 años antes de Cristo, aplicando un método de geometría euclidiana para calcular este valor Irracional. En efecto, Arquímedes buscó una forma de calcular la relación, - ya conocida en ese tiempo-, que existe entre el perímetro de una circunferencia y su diámetro, usando polígonos regulares inscritos o circunscritos. Arquímedes seguramente aplicó el valor $\large{\frac{7}{5}}$ $= 1.4$ para estimar $\sqrt{2}$, dado que los números irracionales no eran formalmente conocidos alrededor del 300 a.C., los geómetras griegos sí sabían que existían longitudes que no podían expresarse como razón de enteros, especialmente desde el descubrimiento de la irracionalidad de $\sqrt{2}$ atribuido a los pitagóricos (siglo V a.C.). El sorprendente resultado fue una estimación de la constante mucho más aproximada que todas las estimaciones anteriores. Valor que incluso se usa hasta hoy, en matemática, física y todas las ciencias que requieren este número. En los siglos anteriores a Arquímedes, la aproximación de la constante $\large{\pi}$ mediante los números racionales $\mathbb {Q}$ de la forma $\frac{p}{q}$ con $p,q \in \mathbb {Z^{+}}$ se realizaban previamente desde hace centenas de años de manera bastante apropiada, especialmente para cálculos constructivos sin usar notación decimal, sino midiendo la precisión estrechando la diferencia entre dos fracciones para ir acotando un valor. Es decir, los matemáticos griegos usaban fracciones racionales entre números enteros, relaciones geométricas expresadas como proporciones, evitaban cálculos aritméticos complejos y, en su lugar, representaban los números mediante longitudes, áreas o volúmenes, aproximaciones por exceso y defecto acotándolo entre dos fracciones7: $$ \frac{223}{71} < \pi < \frac{22}{7} $$ Arquímedes comenzó a aproximar esta longitud en una circunferencia de un radio dado (asumamos $r=1$), con un método muy utilizado para calcular áreas y perímetros desde hace cientos de años, que es dividir y medir en pedacitos regulares y después sumar. Por tanto, el problema de Arquímedes se reducía a calcular el perímetro de una circunferencia, porque que el diámetro está dado de acuerdo a la construcción elegida. Es decir, diámetro $2·r=2$. Desde esa construcción, Arquímedes fue inscribiendo polígonos regulares en dicha circunferencia y calculando su perímetro, llegando a tener cálculos de un polígono inscrito de 96 lados, partiendo desde el cuadrado. (Nótese que este mismo método se puede aplicar desde fuera de la circunferencia, armando una envolvente de polígonos regulares circunscritos). Proceso Geométrico de Arquímedes A partir del cuadrado, Arquímides fue estimando el perímetro de la circunferencia (como si fuera el perímetro del polígono inscrito) y dividiéndolo por el diámetro. Es decir, en cada iteración, calculaba la longitud del lado y el número de lados del polígono, y por tanto, - multiplicando estas dos cifras-, el perímetro estimado, el cual lo dividía por el diámetro dado. 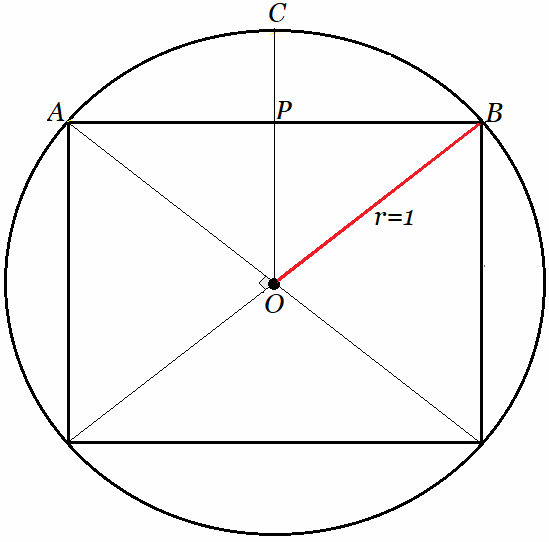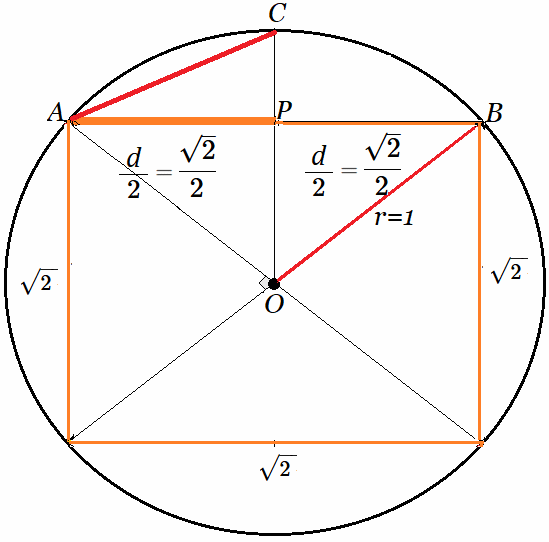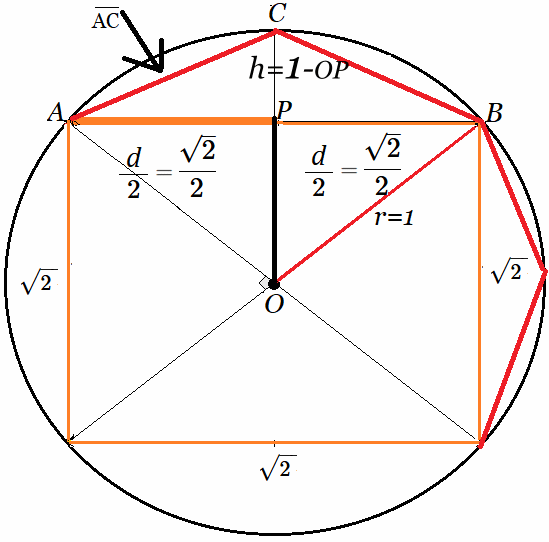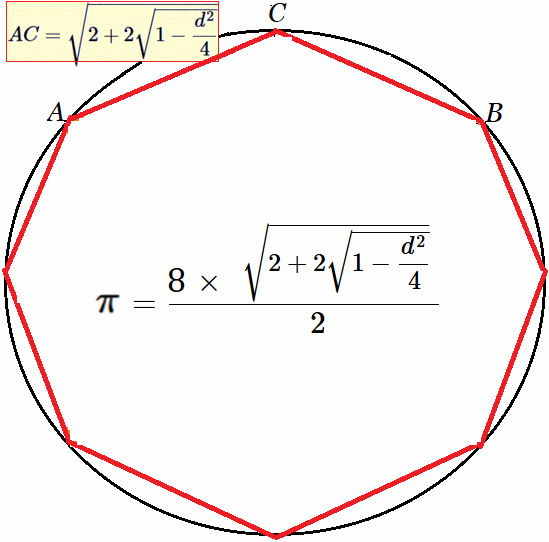 Método de Estimación8 En la figura tenemos un círculo de radio $1$, donde el cuadrado inscrito tiene lado $\sqrt{2}$, dado que en el triangulo rectángulo $AOB$ se tiene: $$ AB^2= \underbrace{AO^2}_{1} + \underbrace{OB^2}_{1}\\ \text{ }\\ AB^2 = 2\\ \implies \\ AB = \large{\sqrt{2}}$$ Sea $\large{d = AB = \sqrt{2}}\quad$ (Las iteraciones en algoritmo, se harán en función del parámetro $\large{d}$, longitud que será la base de la siguiente cuerda o lado del polígono duplicado) Ahora, consideremos la línea $\overline {OC}$ pasando por el punto $P$. Esta línea divide en la mitad el segmento $\overline{AB}$ y permite calcular el lado $\overline {AC}$ del siguiente polígono regular de $8$ lados (primera iteración) y así sucesivamente se irá duplicando el numero de lados del polígono. Por tanto, $$ AC^2=AP^2 + CP^2 \quad \land \quad AP=\large{\left(\frac{d}{2}\right)}=\large{\left(\frac{\sqrt{2}}{2}\right)}\\ \text{ }\\ CP = OC - OP\\ \text{ }\\ CP = 1 - OP \quad \land \quad OC=1\\ \text{ }\\ OP^2 = OA^2 - AP^2,\\ \text{ }\\ \implies\\ \text{ }\\ OP^2=1-\left(\frac{\sqrt{2}}{2}\right)^2\\ \text{ }\\ OP=\sqrt{1-\left(\frac{\sqrt{2}}{2}\right)^2}\\ \text{ }\\ OP=\sqrt{1-{\frac{d^2}{4}}}\\ $$ Ahora que conocemos ambos catetos del triagulo ACP, cuya hipotenusa es el lado del polígono regular de 8 lado que se esta calculado, se tiene: $$CP = 1 - OP \quad \implies \quad CP^2=1 -2·OP + OP^2 \quad \land \quad AP=\large{\frac{d}{2}}$$ Entonces, se calcula el lado $\overline{AC}\quad$ (Segmento rojo en la Figura 1): $$ AC^2=AP^2 + CP^2 \\ $$ Sustituyendo esta última expresión en función del parámetro $\large{d},\quad$ se obtiene: $$ AC^2= \left(\large{\frac{d^2}{4}}\right) + 1 - 2\sqrt{1-\left(\frac{\sqrt{2}}{2}\right)^2} + \left(1-\left(\frac{\sqrt{2}}{2}\right)^2\right)\\ \text{ }\\ AC^2=\large{\frac{d^2}{4}} + 1 + 1 -\large{\frac{d^2}{4}} + 2\sqrt{1-\frac{d^2}{4}}\\ \text{ }\\ AC^2=\require{cancel}{ \cancel{\large{\frac{d^2}{4}}} + \underbrace{ 1 + 1}_2 - \cancel{\large{\frac{d^2}{4}}} + 2\sqrt{1-\frac{d^2}{4}}}\\ \text{ }\\ AC^2= 2 + 2\sqrt{1-\frac{d^2}{4}}\\ \text{ }\\ AC=\sqrt{2 + 2\sqrt{1-\frac{d^2}{4}}} $$ A partir del valor $\overline {AC}$, que representa la longitud del lado del polígono regular (y el diámetro igual $2$), obtendremos el valor de $$ \large{\pi}\approx \frac{n \times \text{ lado del polígono}}{2} $$ Así sucesivamente, se duplica el polígono regular inscrito en la circunferencia, se calcula la nueva longitud del lado en función de $\large{d}$ y el número de lados $n$, de ese modo cada vez se obtiene una aproximación de $\large{\pi}$ más certera. Diagrama de Flujo del Algoritmo
- Descripción Diagrama de Flujo y Función Calculo_Pi()
¿Cuál es el papel de $\large {d}$ en la rutina? $\large {d}$ es la longitud del lado del polígono inscrito en la circunferencia, y se actualiza en cada iteración para reflejar el nuevo polígono con el doble de lados. Este valor se usa para calcular el perímetro y, por lo tanto, mejorar la aproximación de $\large{\pi}$. Ecuación de Difrencias no Lineal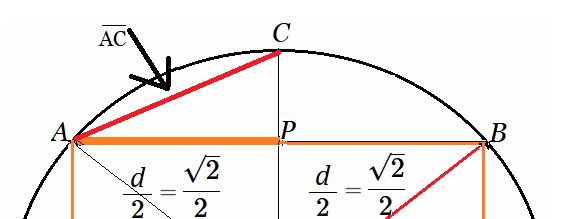 
$$ AC = \sqrt{2 + 2\sqrt{1 - \frac{d^2}{4}}}\qquad\quad[1] $$ La ecuación $[1]$ representa una ecuación de diferencias, ya que define una sucesión donde cada término se calcula en función del anterior. En este caso, la ecuación modela la evolución de la longitud del lado de los polígonos inscritos en la circunferencia, permitiendo mejorar la aproximación de $\large{\pi}$ al calcular el perímetro en cada iteración. En efecto, la ecuación $[1]$ define la longitud del lado del polígono inscrito después de duplicar el número de lados en cada iteración. Como $\large{d}$ representa la longitud del lado del polígono en la iteración anterior, esta ecuación establece una relación recursiva entre la longitud del lado del polígono en dos iteraciones consecutivas. Esta ecuación puede considerarse una ecuación de diferencias no lineal, ya que describe una sucesión donde cada término depende del valor anterior. En términos generales, una ecuación de diferencias se expresa como: $$ d_{n+1} = f(d_n), $$ lo que encaja con la forma de la ecuación $[1]$, pues determina $ AC $ (el nuevo valor del lado del polígono) en función del valor anterior $\large{d}$. Cada vez que se duplica el número de lados del polígono, la nueva longitud del lado $\large{d_{n+1}} $ se obtiene mediante la ecuación: $$ d_{n+1} = \sqrt{2 + 2\sqrt{1 - \frac{d_n^2}{4}}} $$ Donde, existe una relación recursiva:
- $ d_{n+1} $ es la longitud del lado en la siguiente iteración. |
|
Notas Adjuntas
|
| DocIRS © 1988-2025 |