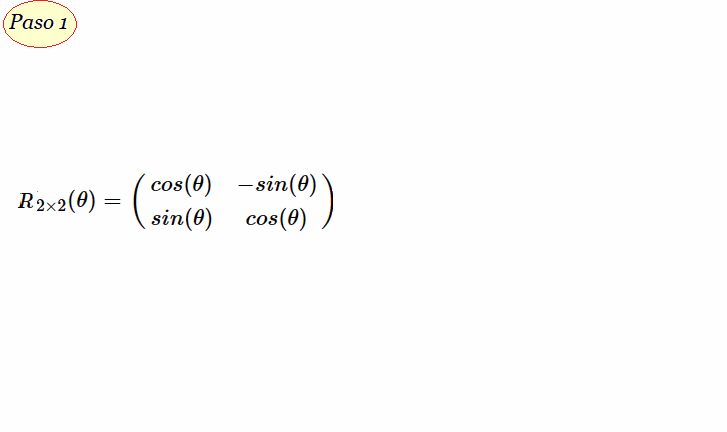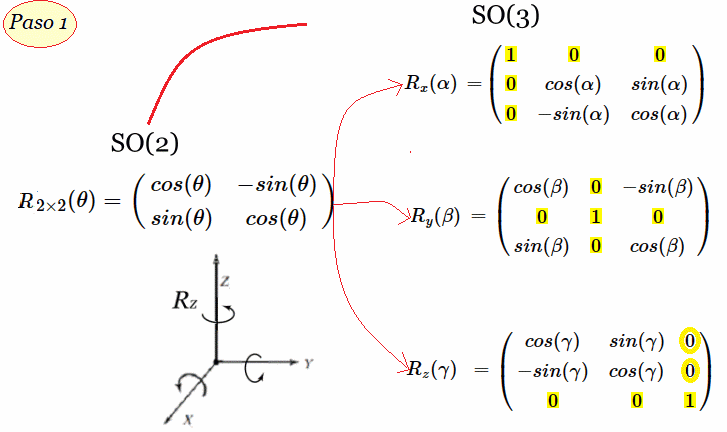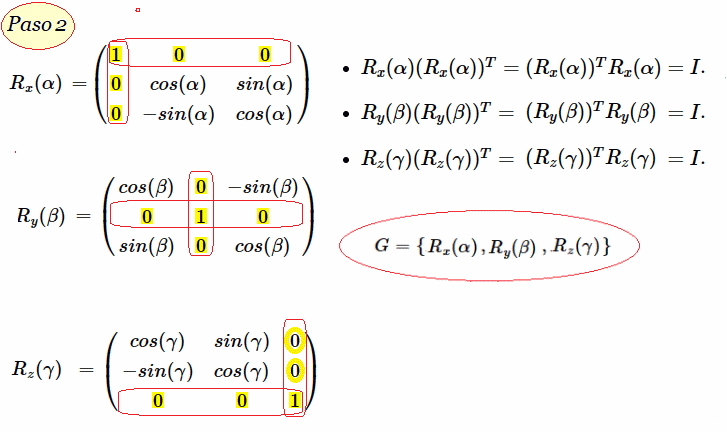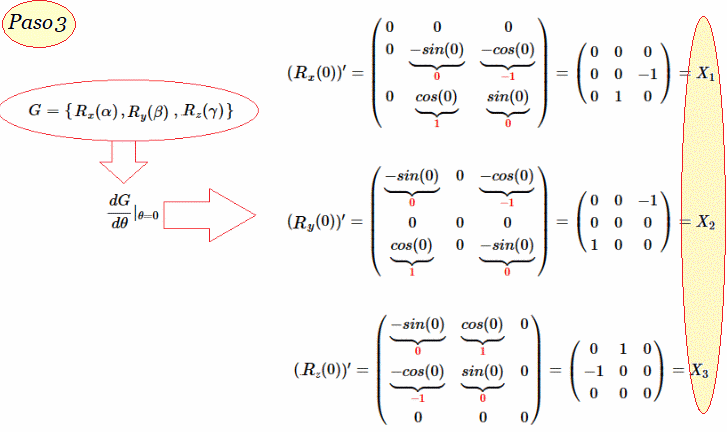Las notas que presentaré a continuación, están relacionadas directamente con los artículos y videos publicados acerca de la Definición del Algebra  de Lie.

El propósito es mostrar la deducción de  las tres matrices unitarias tridimensionales y antisimétricas $\vec P=\unicode{123}X_{1},X_{2},X_{3}\unicode{125}$ que generan el álgebra de Lie $\large{\mathfrak {g}}\equiv$ $\mathfrak {so(3)}$⁸⁹.

Clasificación Grupos Ortogonales $\longrightarrow SO(3)$

Desde lo establecido en los documentos de base, decimos que el álgebra de Lie es una rama matemática que se utiliza en la Teoría de Grupos y la Geometría Diferencial para estudiar las simetrías y transformaciones continuas de objetos matemáticos.

En ese contexto, los grupos de Lie son grupos dotados de una estructura diferenciable. Los generadores del álgebra de Lie son operadores lineales que generan las transformaciones infinitesimales de un grupo de Lie.

Para entender los generadores del álgebra de Lie de $SO(3)$, - que es el grupo de rotaciones especiales en tres dimensiones -, primero debemos comprender la estructura proveniente de $SO(2)$.

$SO(3)$ es un grupo de Lie que representa las rotaciones tridimensionales. Cada elemento de $SO(3)$ es una matriz de rotación $3\times3$ que es ortogonal (su transpuesta es igual a su inversa) y tiene un determinante igual a $1$.

Las rotaciones pueden describirse mediante tres parámetros independientes, que son los ángulos de Euler. Estos ángulos representan las rotaciones alrededor de los ejes $x, y , z$.

Los generadores del álgebra de Lie de $SO(3)$ se relacionan con las transformaciones infinitesimales cerca de la identidad del grupo. Estos generadores se conocen como matrices antisimétricas, y hay tres de ellos, que corresponden a las rotaciones alrededor de los ejes $x, y, z$. Que denotamos como $X_1, X_2, X_3$.

Para comprender mejor estos generadores, podemos expresarlos en términos de los elementos del grupo $SO(3)$.

Supongamos que tenemos una matriz de rotación $R$ en $SO(3)$. Entonces, la representación infinitesimal de la rotación cerca de la identidad se puede escribir como:

$$R(\epsilon) = I + \large{\epsilon} \times X_i \\ \text{Donde, }\large{\epsilon} \longrightarrow 0$$
Donde $\large{\epsilon}$ es un parámetro infinitesimal que representa el ángulo de rotación, $I$ es la matriz de identidad $3\times 3$ y $X_i$ es uno de los generadores del álgebra de Lie. Dependiendo de cuál de los generadores estemos utilizando $X_1, X_2, X_3$, obtendremos una transformación infinitesimal alrededor del eje $x, y , z$ respectivamente.

Estas matrices antisimétricas generan las transformaciones infinitesimales alrededor de los ejes $x, y, z$ respectivamente, en el grupo $SO(3)$. Son los generadores del álgebra de Lie asociados a $SO(3)$ y se utilizan en la Teoría de Grupos de Lie para analizar las propiedades de las rotaciones tridimensionales y las simetrías relacionadas.

Se conmutan estas tres matrices con la operación binaria corchetes de Lie, a fin de obtener los generadores  infinitesimales y sus permutaciones del álgebra de Lie $\large{\mathfrak {g}}$, asociado a los  grupos especiales ortogonales de dimensión $SO(3)$ (Special Orthogonal Group of Dimension 3) ¹⁸⁹.


 Diagrama Proceso Deducción

Proceso Animado Generadores Algebra de Lie
$\large{SO(2) \mapsto SO(3)}$

 Desarrollo $SO(2)\mapsto SO(3)$

Dicho el marco anterior, en la entrada de la  presentación, desarrollaré este complemento pasando desde $SO(2)$ hacia SO(3), con derivación simple sobre las matrices aumentadas tridimensionales de rotación.¹⁸⁷

Los grupos en $SO(3)$ consisten en rotaciones en tres dimensiones, que en este caso se configuraron a partir de la matriz $R_{2 \times 2} \in SO(2)$ aumentada con los vectores canónicos.

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} \mapsto x \mathbf{\vec i} + y \mathbf{\vec j} + z \mathbf{\vec k} $$
Ciertamente la matriz real $R_{2\times 2}$, - sobre un ángulo de rotación $\theta$ -, en torno a un origen o centro de rotación en el plano cartesiano, constituye un generador del Grupo de Lie, i.e. un grupo especial ortogonal de dimensión 2:


$$R_{2 \times 2}(\theta)=\begin{pmatrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \\ \end{pmatrix} $$

A partir de esta matriz de base $R_{2 \times 2}(\theta)$, se construyen las tres matrices generadoras en $SO(3)$, que hemos denotado como $G$, que son:

$$G=\unicode{123} R_{x}(\alpha), R_{y}(\beta), R_{z}(\gamma) \unicode{125}$$
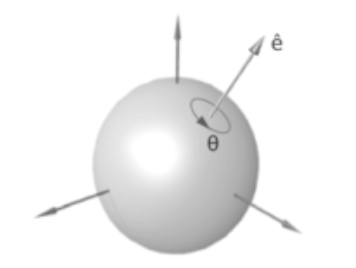
Para la formalización de la rotación de las tres matrices de $G$ en el espacio $\mathbb R^3$, basta sólo con la posición de los vectores unitarios, dado que todo vector es múltiplo de alguno de ellos. Con estos vectores, - y sus operadores matriciales-, se conforma la esfera unitaria.

Permutando cíclicamente los ejes $\vec x, \vec y, \vec z$, obtenemos las representaciones matriciales correspondientes a rotaciones respecto a los ejes.

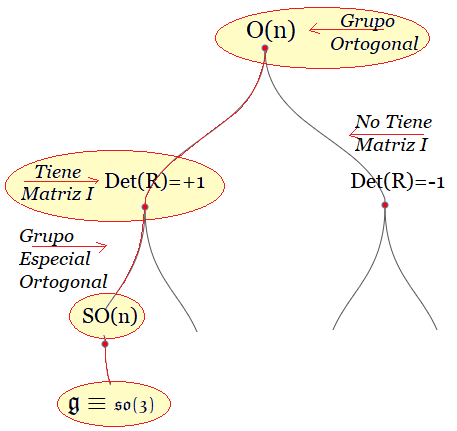
Luego, las matrices de rotación del espacio $\mathbb R^3$ son matrices $3\times 3$, ortogonales y de determinante $1$, i.e. este conjunto tiene estructura de grupo $SO(3)$. En conclusión, el giro es en $SO(2)$ y la acción de rotar la efectúan los elementos del grupo $SO(3)$

Ilustremos la extensión mediante un operador $R_{3 \times 3}(\beta)$ en el plano euclidiano que al ser aplicado a un vector aumentado de coordenadas rectangulares $(x_1,x_2,1)$, - localizado en torno a un punto de origen $0$ -, lo hace rotar en un ángulo $\beta$ hacia un vector $X'$ de coordenadas $(x_1',x_2',1)$.

En otros términos, se aplica el mismo procedimiento previo de SO(2), i.e. una matriz aumentada $R_{3 \times 3}$ que multiplicada por el vector $X$ obtenga estas nuevas coordenadas en $X'$, i.e. de esta forma obtendremos un sistema de coordenadas sobre la variedad SO(3):

$$ X'=\begin{pmatrix} x_{11}'\\ x_{21}' \\ 1 \\ \end{pmatrix}=\begin{pmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \\ \end{pmatrix} \begin{pmatrix} x_{11}\\ x_{21} \\ 1 \\ \end{pmatrix} $$

Este conjunto de matrices cumple las condiciones de rotación en el plano euclidiano y constituye un Grupo de Lie en $SO(3)$.

Rotaciones Independientes en Torno a Ejes ⁸²

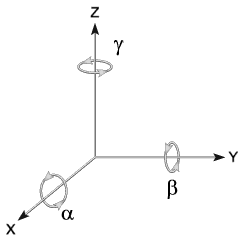
Estas tres matrices de rotación $G=\unicode{123}R_{x}(\alpha), R_{y}(\beta), R_{z}(\gamma)\unicode{125}$ , que se señalan a continuación en $\mathbb R^3$:

• $R_{x}(\alpha)$ rota el plano yz alrededor del origen por un ángulo $\alpha$.


• $R_{y}(\beta)$ rota el plano xz alrededor del origen por un ángulo $\beta$.


• $R_{z}(\gamma)$ rota el plano xy alrededor del origen por un ángulo $\gamma$.

La transpuesta $R^T$ de cada una de estas matrices y multiplicarlas por sus transpuestas respectivas, sus productos serán iguales en a la matriz identidad $I$:

• $R_{x}(\alpha)(R_{x}(\alpha))^T=(R_{x}(\alpha))^T R_{x}(\alpha)=I$.


• $R_{y}(\beta)(R_{y}(\beta))^T=(R_{y}(\beta))^T R_{y}(\beta)=I$.


• $R_{z}(\gamma)(R_{z}(\gamma))^T=(R_{z}(\gamma))^T R_{z}(\gamma)=I$

 Matrices Aumentadas ~ $G \in SO(3)$

Es decir, el grupo completo $G \in SO(3)$ consiste en el producto de estas matrices, las cuales al multiplicarlas por sus transpuestas son iguales a la matriz identidad $I$. Por tanto, cumplen con la condición de ortogonalidad en lo reales:

$$R_{x}(\alpha)= \begin{pmatrix} \bbox[yellow]{1} & \bbox[yellow]{0} & \bbox[yellow]{0}\\ \bbox[yellow]{0} & cos(\alpha) & sin(\alpha) \\ \bbox[yellow]{0} & -sin(\alpha) & cos(\alpha)\\ \end{pmatrix} $$

$$R_{y}(\beta)= \begin{pmatrix} cos(\beta) & \bbox[yellow]{0} & -sin(\beta) \\ \bbox[yellow]{0} & \bbox[yellow]{1} & \bbox[yellow]{0}\\ sin(\beta) & \bbox[yellow]{0} & cos(\beta)\\ \end{pmatrix} $$

$$R_{z}(\gamma)= \begin{pmatrix} cos(\gamma) & sin(\gamma) & 0 \\ -sin(\gamma) & cos(\gamma) & 0 \\ \bbox[yellow]{0} & \bbox[yellow]{0} & \bbox[yellow]{1}\\ \end{pmatrix} $$

Las rotaciones se realizan sobre los ejes de coordenadas cartesianas en el espacio tridimensional euclidiano, se identifican los ángulos de rotación en torno a cada eje, tomando como referencia el giro en torno al eje $z$ como $\gamma$, el giro en torno al eje $y$ como $\beta$, y el giro en torno al eje $x$ como $\alpha$.

Cada una de las tres matrices $R_x(\alpha), R_y(\beta) \text{ y } R_z(\gamma)$ son matrices ortogonales, i.e. dejan invariante la longitud del vector en rotación. Esto se realiza porque se requieren,- en cada plano -, sólo rotaciones en torno a dos de los ejes coordenadas rectangulares, prescindiendo del otro eje.

Nótese que la matriz $R_{2 \times 2}\in SO(2)$ se aumenta introduciendo los vectores canónicos: en el caso $R_{x}(\alpha)$, se introdujo $\vec i$ en la primera fila y primera columna; en $R_{y}(\beta)$ se introdujo $\vec j$ en la segunda fila y segunda columna; y en $R_{z}(\gamma)$ se introdujo $\vec k$ en la tercera fila y tercera columna.

Estas tres rotaciones son independientes las unas de las otras.

Luego, al diferenciar cada una de estas tres matrices y evaluarlas en $\theta=0$, se obtienen los generadores infinitesimales de rotación, en torno a cada uno de los ejes respectivamente $\vec P=\unicode{123}X_{1},X_{2},X_{3}\unicode{125}$ en $SO(3)$. i.e las siguientes derivadas: $\frac{dR_x}{d\alpha}, \frac{dR_y}{d\beta}, \frac{dR_x}{d\gamma}$. (Sabiendo que $sin'(\theta)=cos(\theta),\quad cos'(\theta)=-sin(\theta) \quad \land \quad sin(0)=0,\quad cos(0)=1$)

Entonces, $\vec P=\unicode{123}X_{1},X_{2},X_{3}\unicode{125}$ es un generador unitario del Algebra de Lie en tres dimensiones, el cual se obtiene de las derivadas de cada una de estas tres matrices $R_{x}(\alpha), R_{y}(\beta), R_{z}(\gamma)$.

En efecto,

$$\frac{dG}{d\theta} \mid_{\theta=0}$$ $$(R_{x}(0))'=\begin{pmatrix} 0 & 0 & 0\\ 0 & \underbrace{-sin(0)}_{\color{red} 0} & \underbrace{-cos(0)}_{\color{red} {-1}} \\ 0 & \underbrace{cos(0)}_{\color{red} 1} & \underbrace{sin(0)}_{\color{red} 0}\\ \end{pmatrix}=\begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \\ \end{pmatrix}=X_{1} $$

$$(R_{y}(0))'=\begin{pmatrix} \underbrace{-sin(0)}_{\color{red} 0} & 0 &\underbrace{-cos(0)}_{\color{red} {-1}} \\ 0 & 0 & 0\\ \underbrace{cos(0)}_{\color{red} 1} & 0 & \underbrace{-sin(0)}_{\color{red} 0}\\ \end{pmatrix}=\begin{pmatrix} 0 & 0 & -1 \\ 0 & 0 & 0\\ 1 & 0 & 0\\ \end{pmatrix}=X_{2} $$

$$(R_{z}(0))'=\begin{pmatrix} \underbrace{-sin(0)}_{\color{red} 0} & \underbrace{cos(0)}_{\color{red} 1} & 0 \\ \underbrace{-cos(0)}_{\color{red} {-1}} & \underbrace{sin(0)}_{\color{red} 0} & 0 \\ 0 & 0 & 0\\ \end{pmatrix}= \begin{pmatrix} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 0\\ \end{pmatrix}=X_{3} $$

 Fin de la Deducción de $\vec P$

De esa forma se demuestra cómo se deducen los generadores unitarios del Algebra de Lie $\large{\mathfrak {g}}$ en tres dimensiones $\vec P=\unicode{123}X_{1},X_{2},X_{3}\unicode{125}$, el cual se mapea como $SO(2)\mapsto SO(3)$, i.e. aumentandando la matriz $R_{2\times 2}$ con los vectores canónicos y obteniendo tres matrices $R_{3\times 3}$ de rotación, en torno a cada eje. Posteriormente, se deriva cada una de las matrices de rotación $G=\unicode{123} R_{x}(\alpha), R_{y}(\beta), R_{z}(\gamma) \unicode{125}$, cada una de estas derivadas se evalúa en $0$, y de ahí se obtiene $\vec P$.