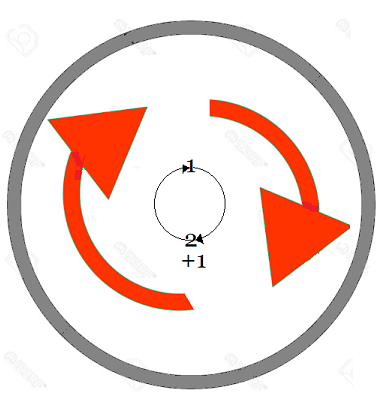
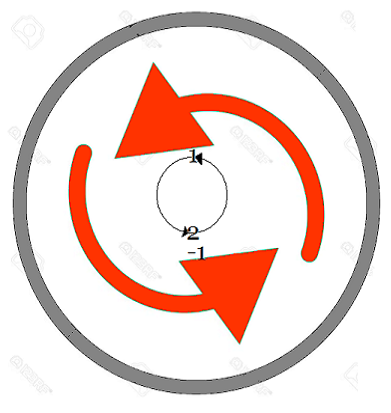
Simple Concepto de Grupo
Cubo de Rubik
José Enrique González Cornejo
mayo 2025
|
Video Asociado
|
Prefacio
En el primer curso de Álgebra Moderna se introduce la Teoría de Conjuntos, abordando el concepto de colecciones de objetos y comenzando con los conjuntos numéricos más conocidos Naturales, Enteros, Racionales, Reales y Complejos ($\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C} $). 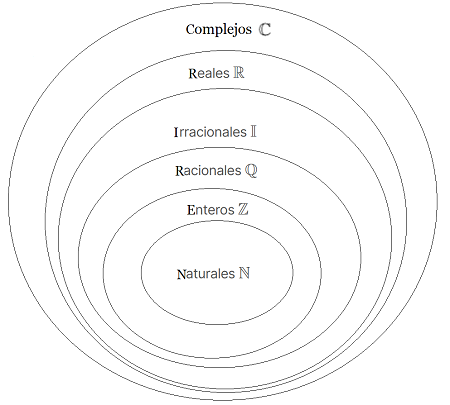Se trata de conjuntos en los cuales es posible combinar dos elementos mediante operaciones como la suma o la multiplicación, obteniendo siempre un nuevo elemento dentro del mismo conjunto. Los elementos de estos conjuntos pueden ser números, funciones u otros objetos, ya que las técnicas algebraicas aplicadas son similares. A medida que se definen una o más operaciones sobre un conjunto (como la suma o la multiplicación), surgen las llamadas estructuras algebraicas básicas, entre las que destacan los Grupos, Anillos, Cuerpos y Campos. Estas estructuras algebraicas se organizan de acuerdo con el número y tipo de operaciones definidas, y se caracterizan por cumplir ciertas propiedades fundamentales, tales como asociatividad, conmutatividad, existencia de identidad, inversos, clausura, entre otras. 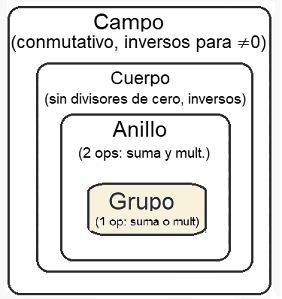 En general, las asignaturas introductorias de Álgebra Moderna presentan una visión inicial de estos conceptos, enfocándose particularmente en las operaciones binarias y en el estudio del concepto de Grupo mediante ejemplos simples, como las tablas modulares en el conjunto de los enteros positivos $\mathbb {Z^{+}}$.
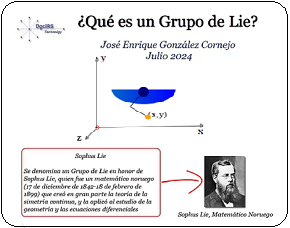
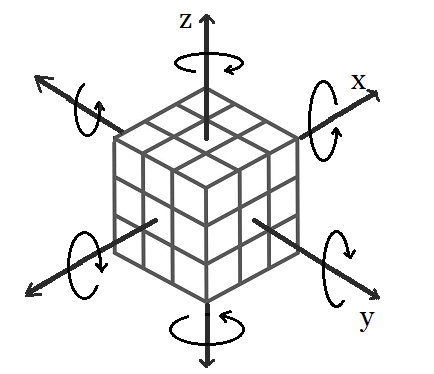
Introducción En esta presentación, mi objetivo es intentar explicar de forma didáctica el concepto de Grupo, utilizando como recurso ilustrativo un objeto físico ampliamente conocido: el Cubo de Rubik. Supongamos tenemos en nuestras manos un cubo clásico de Rubik. Es decir, un cubo de 6 caras con 9 cubitos o stikers en cada una de ellas, con 8 vértices como se ilustra en la figura.
Permutaciones Luego, se define una rotación de una de sus seis caras, donde cada movimiento es una permutación. Así mismo, no hacer nada o ejecutar varios movimientos seguidos continúan siendo una permutación. El grupo de permutaciones de $A$, llamado también el grupo simétrico sobre $A$, i.e. es el conjunto de todas las permutaciones que se pueden realizar sobre si mismo en una relación 1-1 y sobre: $$ \mathcal{S}(A) = \{ g\colon A\to A\ |\ g \mbox{ es biyectiva} \} $$ Ahora, con la composición de funciones como operación se tiene la siguiente definición: Sea $(S_{A},\circ)$ el cubo de Rubik descrito con todos sus elementos giratorios, donde "$\pmb {\circ}$" representa la operación de rotación que se ejerce sobre el objeto. Luego, el conjunto de rotaciones que se pueden realizar en una sola cara del cubo de Rubik. Considérese un cubo de Rubik y las rotaciones que se pueden realizar en él, donde el conjunto de rotaciones que se pueden realizar en una sola cara del cubo de Rubik. Operación Binaria La operación binaria en este conjunto es la composición de rotaciones. Es decir, si tenemos dos rotaciones $\mathit {r_1}$ y $\mathit {r_2}$, la composición $\mathit {r_1 \circ r_2}$ se define como la rotación resultante de aplicar primero $\mathit{r_1}$ y luego $\mathit{r_2}$.
Propiedades Estos giros, movimientos o rotaciones sobre todos elementos que se pueden realizar en el cubo de Rubik, constituyen una operación binaria, que cumple con todas las propiedades requeridas:
 Por tanto, el conjunto de movimientos del cubo de Rubik con la composición de movimientos forma un Grupo, más específicamente una estructura algebraica llamada Grupo de Permutaciones, cuya composición de movimientos es una operación binaria que satisface la propiedades del Algebra de Grupos.  Estos giros de cara del cubo de Rubik mediante una permutación animada de los vértices es un grupo de permutación, dado que es un conjunto de elementos y un conjunto de operaciones que reordenan esos elementos, constituyen un grupo que cumple con las propiedades mencionadas de una operación binaria. Es decir, aplicada una permutación tras otra es también una permutación válida, el orden de agrupación de operaciones no importa, existe una permutación que deja todo igual y toda permutación tiene una que la deshace. 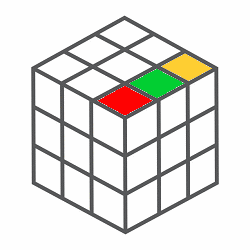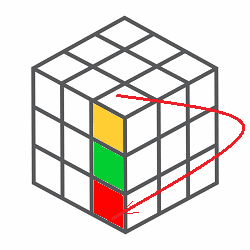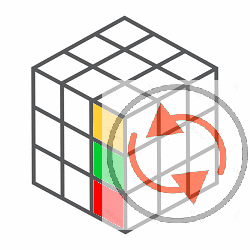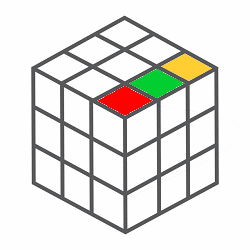 Rotación - Inversa 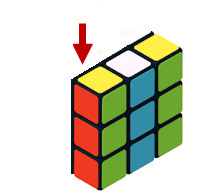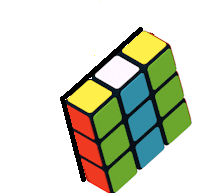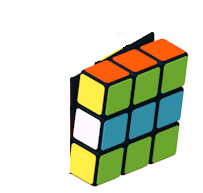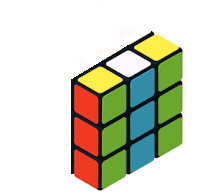 Rotación-Completa (Identica) Grupo de Permutación Un grupo de permutación es un conjunto de elementos y un conjunto de operaciones que reordenan esos elementos, cumpliendo las propiedades de grupo. En el caso del cubo de Rubik, como se ha mostrado se los elementos del grupo son las piezas móviles con centros fijos, donde cada movimiento permuta (reorganiza) las piezas del cubo. Sus ecuencias de movimientos forman un grupo. Agregar que este grupo de prermutaciones de no cumple con la propiedad conmutativa, es dicir es no abeliano, porque el orden de los elementos cuando se aplican las permutaciones en una operación, esto afecta el resultado final.
|
| DocIRS © 1988-2025 |