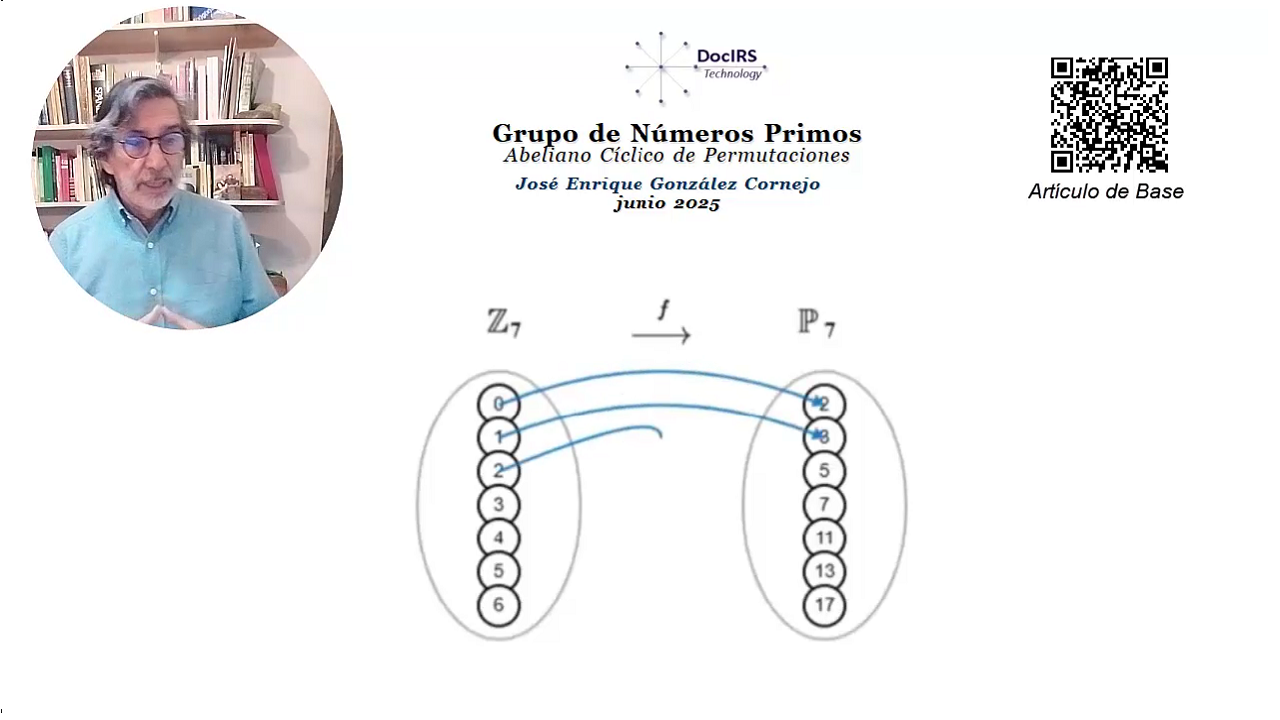
Grupo de Números Primos
Abeliano Cíclico de Permutaciones
José Enrique González Cornejo
junio 2025
|
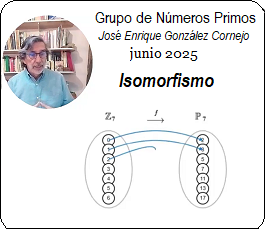
| $\Large{\mathbb {Z}}$ $\qquad\qquad \require{AMScd} \Large{ \begin{CD} @>{\textit{f}}>> \end{CD} } \qquad\qquad \Large{\mathbb {P}}$ |
| $\quad p_i \ast p_j := f\left( (i + j) \bmod n \right)$ |
|
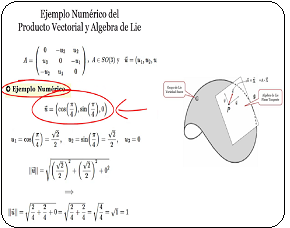
Introducción En este trabajo se propone la construcción de una estructura algebraica de grupo finito, compuesta exclusivamente por números primos, mediante la definición de una operación binaria artificial basada en la suma modular de índices. Dado que el conjunto de los números primos no es cerrado bajo las operaciones aritméticas tradicionales como la suma o la multiplicación, se plantea una operación especial que permita dotar a un subconjunto finito de primos de estructura de grupo. (Ver Simple Concepto de Grupo ~ Cubo de Rubik Sea $\mathbb{P}_n = \{p_0, p_1, \dots, p_{n-1}\} \subset \mathbb{P}$, una secuencia ordenada de $n$ números primos, con $n \gt 4$. Se define una biyección $f: \mathbb{Z}_n \rightarrow \mathbb{P}_n$, y con ella, una operación binaria artificial "$\large{\ast}$" sobre $\mathbb{P}_n$, dada por: $$ p_i \ast p_j := f\left( (i + j) \bmod n \right) $$ Esta operación, definida sobre los índices de los primos, hereda las propiedades algebraicas del grupo cíclico $(\mathbb{Z}_n, +)$. En consecuencia, el conjunto $(\mathbb{P}_n, \ast)$ constituye un grupo abeliano cíclico, es decir, una estructura cerrada, asociativa, con elemento neutro e inversos, y conmutativa. Por ende, se intenta exponer la fundamentación teórica de esta construcción, ilustrando cómo la operación artificial define una Tabla de Cayley que representa todas las combinaciones posibles bajo la operación "$\large{\ast}$". Finalmente, se implementa un algoritmo en JavaScript que permite generar dinámicamente la Tabla de Cayley, para cualquier valor de $n \gt 4 \quad \land \quad n \lt 100 $ , posibilitando así la visualización interactiva de este tipo particular de grupos de permutaciones. Grupo de Números Primos Luego, sea $(\large{\mathbb {P}_n,\ast)}$ un grupo1 de números primos dotado de una operación binaria "$\large{\ast}$" asociada, de tal manera que $p \ast q = w$, donde $p,q,w \in \mathbb P$ , que se presentará en este artículo. Donde $\mathbb {P}$ es el conjunto de números primos: $$ \bbox[white,12px,border:1px solid #c0c0c0] { \large{\mathbb{P} = \{ p \in \mathbb{N} \mid p > 1 \quad\land\quad \forall d \in \mathbb{N},\ (d \mid p \Rightarrow d = 1\quad \lor \quad d = p) } } \qquad \large{[1]} $$ En otras palabras, cada número primo $\large{p}$ pertenece al conjunto de los números naturales. Por definición, los números primos son mayores que $1$, y un número $\large{p}$ es primo si sus únicos divisores naturales ($d$) son $1$ y $\large{p}$ mismo. A continuación, se diseña una operación artificial, que denotaremos por "$\large{\ast}$", la cual cumple con todas las propiedades requeridas de una operación binaria sobre un determinado conjunto de números primos. Esta operación se denomina artificial porque los números primos no forman un grupo bajo operaciones naturales como la suma o la multiplicación. En efecto, al operar dos números primos mediante las operaciones ordinarias, ya sea suma o multiplicación, el resultado no suele ser un número primo. Por ejemplo: $5 + 7 = 12 \notin \mathbb{P}$. La suma de dos primos no siempre produce un número primo, ya que no cumple con la propiedad de clausura3. Es decir, la suma de dos primos no está cerrada en el conjunto $\mathbb{P}$, ya que frecuentemente resulta en números compuestos. Esto concuerda con la Conjetura de Goldbach2, que postula que muchos números pares (compuestos) pueden expresarse como la suma de dos primos. Por tanto, no es posible definir un grupo sobre los enteros positivos mayores que $4$ compuesto exclusivamente por números primos utilizando operaciones binarias habituales como la suma o la multiplicación. Por ello, se hace necesario definir una operación artificial que permita construir un grupo cerrado de permutaciones. Operación Binaria Artificial $$ \bbox[white,12px,border:1px solid #c0c0c0] { p_i \ast p_j = f\left( (i + j) \bmod n \right)\qquad \large{[2]} } $$ La operación binaria artificial "$\large {\ast}$" se aplicará para generar una estructura algebraica que satisface las propiedades de grupo $ \ast : \mathbb {P}_n \times \mathbb {P}_n \to \mathbb {P}_n $, tal que $(\mathbb {P}_n, \ast)$ forme un grupo finito, donde:
Nótese que el conjunto $\mathbb{P}_n$ contiene solo números primos, el comportamiento bajo la operación "$\large{\ast}$" no preserva propiedades aritméticas de primos como primalidad o divisibilidad. Solo se comporta como un grupo abstracto bajo la operación $\large{[2]}$. Esta transformación $\large{f}$ biyectiva permite generar permutaciones estructuradas sobre conjuntos de primos y visualizar operaciones de grupo (tablas de Cayley). Ejemplo Aplicación con $\large{\mathbb{P}_5}$ $$ \large{\mathbb{P}_5 = \{2, 3, 5, 7, 11\}}\\ \text{ }\\ f(0)=2,\text{ }f(1)=3,\text{ }f(2)=5,\text{ }f(3)=7,\text{ }f(4)=11\\ \text{ }\\ f(2+4) =f(6\quad mod\quad 5)= f(0)=2 $$ 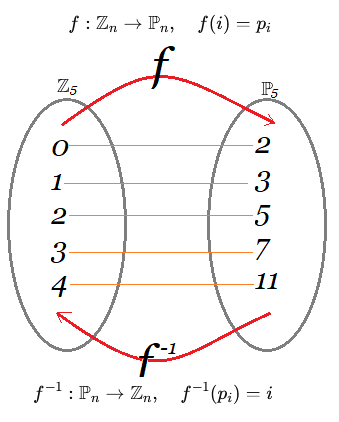
Los 5 índices $\{0,1,2,3,4\}$ se asignan biyectivamente a las secuencia de números primos de $ \large{\mathbb{P}_5 = \{2, 3, 5, 7, 11\}}$
Demostración Operación Binaria Por demostrar que "$\large {\ast}$" es una operación binaria sobre el conjunto de números primos: $$ \large{ p_i \ast p_j = f\left( (i + j) \bmod n \right) }$$ $$ \large{ \mathbb{P}_n = \{p_0, p_1, \dots, p_{n-1}\} \subset \mathbb{P}, \quad \text{con } n > 4 } $$ Es decir en $\large{[2]}$, se definió una función de indexación que es una una biyección: $$ f : \mathbb{Z}_n \to \mathbb{P}_n, \quad f(i) = p_i $$ Luego, su inversa es: $$ f^{-1} : \mathbb{P}_n \to \mathbb{Z}_n, \quad f^{-1}(p_i) = i $$ Es decir: Se verifica que $\large{\ast}$ es binaria, dado que $p_i \ast p_j \in \mathbb{P}_n$ cumple con las propiedades requeridas:
Luego, $$ \text{ }\\ \forall {p_i, p_j} \in \mathbb{P}_n\\ \text{ }\\ \implies\\ \text{ }\\ \Large{p_i \ast p_j \in \mathbb{P}_n}\\ $$ $(\large{\mathbb {P}_n,\ast)}$ ~ Grupo Abeliano Cíclico de Permutaciones En resumen, $\large{\ast}$ es una operación sobre índices, y como tal se basa en el grupo cíclico $\mathbb Z$ bajo suma módulo $\large{n}$, donde los elementos del grupo (los primos) son etiquetas asociadas a los índices, y heredan la estructura algebraica de los índices. $$ p_i \ast p_j := f\left( (f^{-1}(p_i) + f^{-1}(p_j)) \bmod n \right) $$ con $f: \mathbb{Z}_n \to \mathbb{P}_n$ una biyección, hace que el conjunto $(\mathbb{P}_n, \ast)$ sea un grupo, y que es isomorfo al grupo cíclico $(\mathbb{Z}_n, +)$. En efecto, $(\large{\mathbb {P}_n,\ast)}$ es un grupo porque verifica que es satisface las propiedades de clausura, asociatividad y existencia de elemento neutro e Inversos.
Para todo $p_i, p_j \in \mathbb{P}_n$, $p_i \ast p_j = p_k \in \mathbb{P}_n$. $\implies$ $(i + j) \bmod n$ está en $\{0, 1, ..., n-1\}$ ii) Asociatividad $(p_i \ast p_j) \ast p_k = p_i \ast (p_j \ast p_k)$ $\implies$ La suma modular es asociativa en $\mathbb{Z}_n$. iii) Elemento Neutro5 Existe un $p_e = p_0$ tal que: $p_e \ast p_i = p_i \ast p_e = p_i$ $\implies$ $0 + i \equiv i \pmod{n}$ iv) Elemento Inverso Para cada $p_i$, existe $p_j$ tal que: $ p_i \ast p_j = p_0\\ \Rightarrow (i + j) \equiv 0 \pmod{n}\\ \Rightarrow j \equiv -i \pmod{n} $ $\implies$ Cada elemento tiene un inverso bajo la operación módulo $\large{n}$ v) Conmutatividad $ p_i \ast p_j = p_j \ast p_i $ $\implies$ $(i + j) \bmod n = (j + i) \bmod n$ Por tanto, $(\large{\mathbb {P}_n,\ast)}$ es un Grupo Abeliano de Cíclico de Permutaciones . Algoritmo Matemático ~ Tabla de Cayley Es decir, se construye un algoritmo matemático expresado en funciones de Javascript, que configura una tabla de Cayley con el subconjunto $\mathbb{P}_n$ , donde $ n \in \mathbb {N}, n>4$, de modo de constituir un grupo cíclico de permutaciones. Esto significa que $\mathbb{P}_{n}$ es una serie con de números primos, bajo una relación de orden secuencial6 $ p_{i_1}\lt p_i$, donde $\mathbb{P}_{n}$ está dotado de una operación binaria "$\large {\ast}$", i.e. $\forall p_i \ast p_j = p_k\quad \text{|}\quad p_i,p_j,p_k \in \mathbb{P}_{n}$. La siguiente tabla de Cayley es una matriz de orden $n\times n$, donde se etiquetan tanto la primera fila como la primera columna de la tabla con los números primos definidos en $\mathbb{P}_{n}$ $$ f : \mathbb{Z}_n \to \mathbb{P}_{n}, \quad f(i) = p_i $$ Esta función asigna a cada entero módulo $\large{n}$ un primo único. Sea $p_i = f(i),\text{ } p_j = f(j) \in \mathbb{P}_{n}$. Se definió en $\large{[2]}$, la operación $\large{\ast}$ sobre $\mathbb{P}_{n}$ como: $$ p_i \ast p_j = f\left( (i + j) \bmod n \right) $$ Esto es, se realiza la suma módulo $\large{n}$ sobre los índices y se devuelve el primo correspondiente. Ahora, se construye la tabla de Cayley usando: $$ p_i \ast p_j = f\left( (i + j) \bmod n \right) $$ Grupo Primo de Permutaciones $\large {\mathbb {P}}$ Síntesis Este artículo demuestra que las biyecciones e isomorfismos permiten comparar estructuras algebraicamente equivalentes, lo cual resulta fundamental para simplificar problemas, transferir soluciones entre contextos distintos y reconocer simetrías subyacentes. En particular, para construir una estructura algebraica de grupo finito compuesta exclusivamente por números primos, se definió la función en $\large{[2]}$: $$ f: \mathbb{Z}_n \longrightarrow \mathbb{P}_n $$ Esta función cumple con las siguientes propiedades destacables: |
|
Notas Adjuntas
|
| DocIRS © 1988-2026 |